Числовая прямая, числовые промежутки
Прямую линию с выбранными на ней началом отсчёта, единичным отрезком и направлением называют координатной прямой.
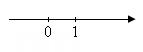
Каждому числу можно поставить в соответствие единственную точку на координатной прямой.
Для числовых промежутков вводят обозначения:
· [a; b] или a≤ х ≤ b – замкнутый промежуток (или отрезок) с началом a и концом b;
· (a; b) или a< х <b - открытый промежуток (интервал);
· (a; b] или a< х ≤ b; [a; b) или a≤ х < b – полуоткрытые промежутки (полуинтервалы);
· [a; + ∞) или х ≥ a; (- ∞; b] или х ≤ b – лучи;
· (a; + ∞) или х >a; (- ∞; b) или х < b – открытые лучи;
· (- ∞; + ∞) = R – координатная прямая.
Модуль числа
Модулем (абсолютной величиной) действительного числа a называется само это число, если a≥ 0, и противоположное число –a, если a< 0. Модуль a обозначается |a|. Итак,
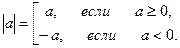
Геометрически |a| означает расстояние на координатной прямой от точки, изображающей число a, до начала отсчёта.
Если a≠0, то на координатной прямой существуют две точки a и –a, равноудалённые от нуля, модули которых равны:
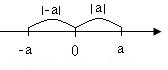
Свойства.
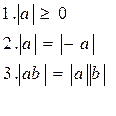
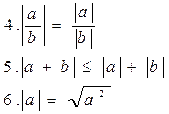
Степень с натуральным показателем. Понятие. Свойства
Степенью числа a с показателем n, где n 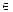 N, а
N, а 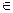 R, называется произведение n множителей, каждый из которых равен a:
R, называется произведение n множителей, каждый из которых равен a: 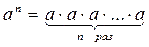 .
.
Число a называется основанием степени, n – показателем степени.
Свойства:
· при умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним
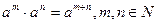
· при делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним 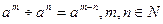
· при возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним
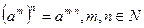
· степень произведения равна произведению степеней множителей 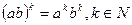
· степень частного равна частному степеней делимого и делителя: 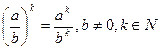
· 
· 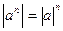
· если 0 ≤ а < b, то 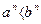
· если а > 1, то 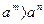 , при m > n.
, при m > n.
· если 0 < а < 1, то 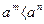 при m > n.
при m > n.
· если а < 0, то 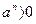 при четном n и
при четном n и 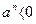 при нечетном n.
при нечетном n.
Утверждения:
· чётная степень отрицательного числа есть число положительное;
· нечётная степень отрицательного числа есть число отрицательное;
· любая степень положительного числа есть число положительное;
· при возведении нуля в любую натуральную степень получается нуль;
· при возведении 1 в любую натуральную степень получается единица.
Степень с целым и дробным (рациональным) показателем.
1. Рассмотрим степень ар, где р 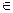 Z.
Z.
Если р=0,то 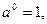 при
при 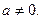
Если р<0, то 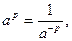 при
при 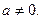
2. Рассмотрим степень 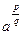 , где
, где 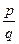 - рациональное число. Выражение
- рациональное число. Выражение 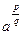 имеет в общем виде смысл только при а>0. Если а>0, р
имеет в общем виде смысл только при а>0. Если а>0, р 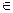 Z, q
Z, q 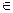 N, то
N, то 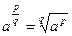 .
.
3. Степень с целым и рациональным показателем обладает теми же свойствами, что и степень с натуральным показателем:
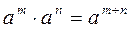 ;
;
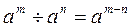 ;
;
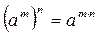 ;
;
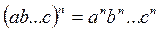 ;
;
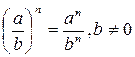 .
.
