Точка. Прямая. Взаимное положение точки и прямой.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
Учреждение высшего образования
«Пермский государственный национальный исследовательский университет»
Кафедра неорганической химии
Рабочая тетрадь
по начертательной геометрии
Выполнил студент_________ группы
_______________________________
«_____»_________________20____
Проверил преподаватель
Исыпова Евгения Александровна
«_____»_________________2017
Пермь 2017
-2-
Принятые обозначения
1. Точки, расположенные в пространстве, - прописными буквами латинского алфавита: А, В, С, ... или цифрами 1, 2, 3, 4....
2. Прямые и кривые линии в пространстве – строчными буквами латинского алфавита: a, b, c, d ....
3. Плоскости – строчными буквами греческого алфавита: α, β, γ ....
4. Поверхности – прописными буквами греческого алфавита: Φ, θ, λ, Σ.
5. Углы – строчными буквами греческого алфавита: φ, ψ, ω.
6. Особые прямые имеют постоянные обозначения:
а) линии уровня: горизонталь – h; фронталь – f;
б) следы плоскости общего положения обозначают той же буквой, что и плоскость с добавлением подстрочного индекса, соответствующего плоскости проекции, например αП1, βП2;
в) следы проецирующих плоскостей:
α1 – горизонтальный след плоскости α ┴ П1,
β2 – фронтальный след плоскости β ┴ П2.
Проецирующие плоскости изображаются только одним следом – тем, который является проекцией данной плоскости на плоскость, ей перпендикулярную;
г) оси вращения – i, j.
7. Плоскости проекций – прописными буквами греческого алфавита: горизонтальная – П1; фронтальная – П2; профильная – П3.
8. Новая плоскость проекций при замене плоскостей проекций – буквой П с добавлением подстрочного индекса: П4, П5, П6 ....
9. Проекции точек, прямых и плоскостей – соответствующей буквой и добавлением подстрочного индекса, указывающего плоскость проекций; на плоскости П1 – А1, а1, α1; на плоскости П2 – А2, а2, α2; на плоскости П3 – А3, а3, α3.
10. Основные операции:
а) совпадение двух геометрических фигур ≡, например, а≡b, А1≡В1;
б) взаимная принадлежность геометрических фигур є, например, А є а, h є α;
в) пересечение двух геометрических фигур ∩, например, а ∩ b, α ∩ β;
г) результат геометрической операции =, например, К = а ∩ b, l = α ∩ β.
-3-
Точка. Прямая. Взаимное положение точки и прямой.
Вопросы для самопроверки
1. Что называется проекцией?
2. Какие три плоскости приняты при ортогональном проецировании?
3. Что называется осью проекций?
4. Что называется эпюром (комплексным чертежом) точки?
5. Что называется линией проекционной связи?
6. Сколько проекций точки определяют ее положение в пространстве?
7. Как может быть расположена прямая относительно плоскостей проекций?
8. Чем характерен эпюр прямой общего положения?
9. Чем характерны эпюры горизонтали, фронтали и профильной прямой?
10. Чем характерны эпюры проецирующих прямых?
11. Как построить на чертеже прямоугольный треугольник для определения длины отрезка прямой общего положения и ее углов к плоскостям П1 и П2.
12. Как разделить отрезок прямой в заданном отношении?
13. Сформулировать признаки, принадлежности точки прямой.
14. Что называется следом прямой линии? Обозначение следов.
-4-
1. Какая из точек А, В, С расположена дальше от плоскости П1; П2; П3? Записать ответ и координаты точек.
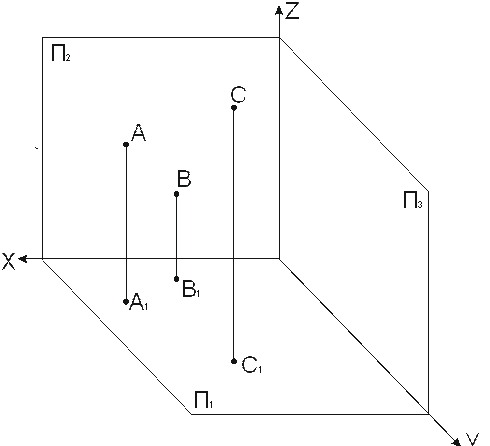
2. Построить проекции: точки В, которая на 5 мм выше точки А и на 20 мм ближе к наблюдателю; точки С, которая расположена справа от точки А на расстоянии 15 мм и ниже ее на 5 мм; точки Д, которая расположена на 15 мм слева от точки А и принадлежит П2. Записать координаты всех точек.
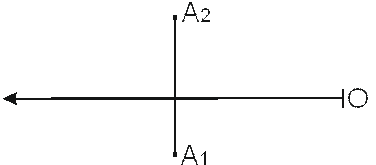
-5-
3. Построить: а) точки А, В, С, Д, расположенные в I, II, III, IV четвертях пространства; б) точки E, F, G, R, расположенные в биссекторных плоскостях
I - III, II – IV; в) точки К и М, соответственно расположенные в нижнем поле фронтальной плоскости и на заднем поле горизонтальной плоскости; г) точку N, расположенную по оси ОХ. Числовые координаты всех точек вписать в таблицу.
| A | B | C | Д | E | F | G | R | K | M | N | |
| X | |||||||||||
| Y | |||||||||||
| Z |

-6-
4. а) Определить натуральную 5. Определить величину отрезка
длину отрезка АВ и угол α; АВ и угол β. б) на отрезке АВ найти точку,
отстоящую от точки В на 20 мм.
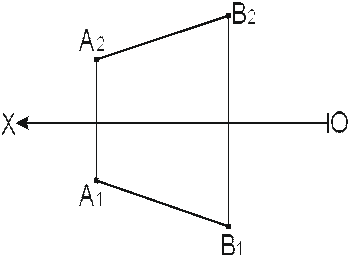
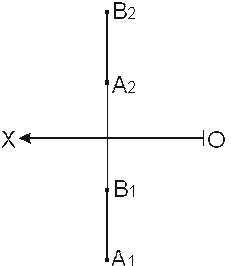
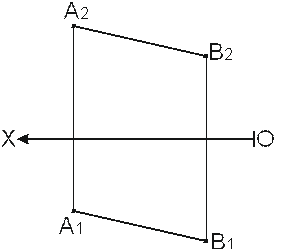
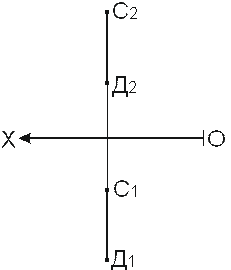
6. Отрезок АВ разделить точкой С 7. Отрезок СД разделить точкой Е так, чтобы АС/СВ = 2/3. так, чтобы СЕ/ЕД = 1/3.
-7-
8. Составить комплексный чертеж отрезков АВ, СД, ЕF, KL и MN по заданным координатам и определить их положение относительно плоскостей проекций:
A (100,50,50), В (40,65,70);
С (85,35,55), Д (25,80,55);
Е (0,84,50), F (75,6020);
K (45,50,15), L (85,50,10);
M (50,55,35), N (50,80,0).
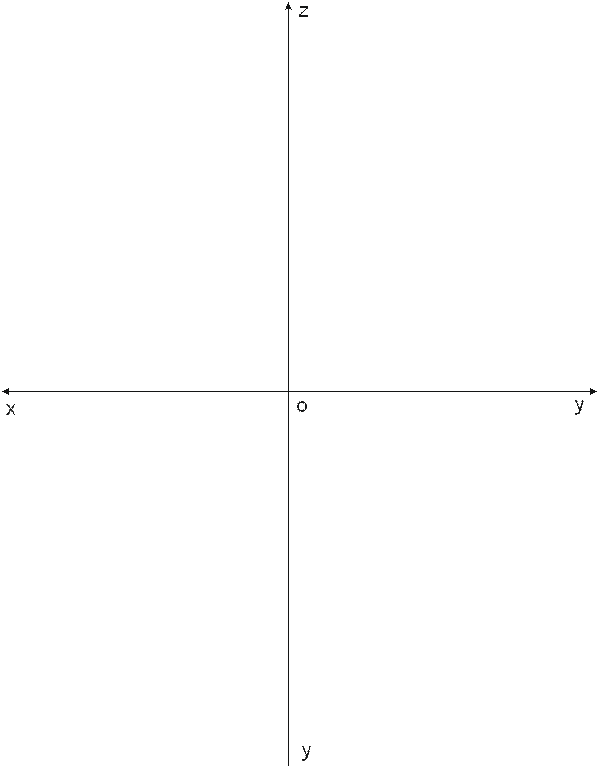
-8-
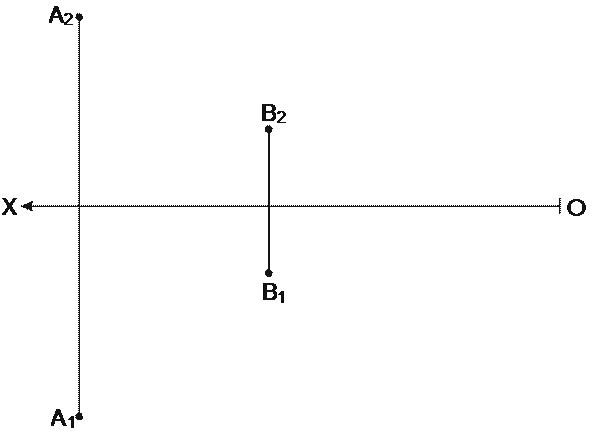
9. Построить следы прямой, определенной точками А и В, указать, через какие четверти пространства она проходит.
-9-
