Схема алгоритма метода простых итераций.

Рисунок 5.1. Схема алгоритма метода простых итераций

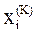Сходимость метода простых итераций можно несколько улучшить, если при вычислении очередного приближения использовать уже найденные значения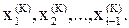

Выражение для расчета очередного к-го приближения примет вид:

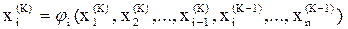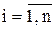, ; (5.11)

Для реализации данного приема, аналогичного методу Гаусса-Зейделя для систем линейных уравнений, в алгоритм расчета следует внести изменения: формулу расчета очередного приближения (символ 5) записать как X=φ(x) или в развернутом виде:

,

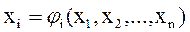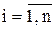
Существуют и другие приемы улучшения сходимости метода простых итераций. Например, новое приближение вычислять как среднее арифметическое двух предшествующих приближений:

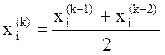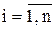, (5.12)

Можно использовать поправку Эйткена для улучшения сходимости:

,

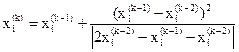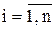
Постановка задачи

Дана система 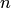нелинейных уравнений с 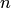неизвестными:

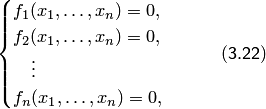
где 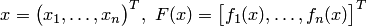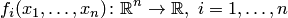, — нелинейные функции, определенные и непрерывные в некоторой области 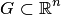, или в векторном виде (где )

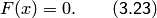
Требуется найти такой вектор 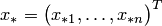, который при подстановке в систему (3.22) превращает каждое уравнение в верное числовое равенство.

Решить методом простых итераций.

для применения метода требуется привести систему (3.22) к равносильному виду:

(3.24)

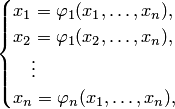
или в векторной форме

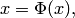
(3.25)

где 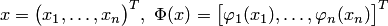, функции 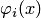определены и непрерывны в окрестности изолированного решения 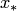системы (3.24).

17.)

Аппроксимацией(приближением) функции 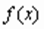называется нахождение такой функции 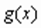(аппроксимирующей функции), которая была бы близка заданной.

Функция f(x), в зависимости от специфики задачи, может отвечать различным требованиям.

· Функция f(x) должна проходить через точки (x_i,y_i), т. е. f(x_i)=y_i ,i=1...n. В этом случае говорят об интерполяции данных функцией f(x) во внутренних точках между x_i, или экстраполяции за пределами интервала, содержащего все x_i.

· Функция f(x) должна некоторым образом (например, в виде определенной аналитической зависимости) приближать y(x_i), не обязательно проходя через точки (x_i,y_i). Такова постановка задачи регрессии, которую во многих случаях также можно назвать сглаживанием данных.

· Функция f(x) должна приближать экспериментальную зависимость y(x_i), учитывая, к тому же, что данные (x_i,y_i) получены с некоторой погрешностью, выражающей шумовую компоненту измерений. При этом функция f(x), с помощью того или иного алгоритма уменьшает погрешность, присутствующую в данных (x_i,y_i). Такого типа задачи называют задачами фильтрации. Сглаживание - частный случай фильтрации.

Критерии близости функци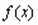й и 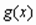могут быть различные.

В том случае, когда приближение строится на дискретном наборе точек, аппроксимацию называют точечной илидискретной.

В том случае, когда аппроксимация проводится на непрерывном множестве точек (отрезке), аппроксимация называется непрерывнойили интегральной. Примером такой аппроксимации может служить разложение функции в ряд Тейлора, то есть замена некоторой функции степенным многочленом.

Типичной задачей аппроксимации функций является задача интерполяции. Необходимость интерполяции функций в основном связана с двумя причинами: