Дискретные случайные величины
| Случайной называют такую величину, которая может принимать различные значения в зависимости от множества случайных обстоятельств, которые учесть практически невозможно. Приведите примеры… |
| Конкретные значения случайной величины называют ….???.... |
| Если варианты отличаются не на любое сколь угодно малое значение – обычно на единицу, то мы имеем дело с дискретной. |
| Если варианты отличаются друг от друга на любое сколь угодно малое значение, то такая случайная величина называется непрерывной. |
| Для любых случайных величин есть три основные характеристики математическое ожидание(М или МО)………………………….. дисперсия(D), ………………………………………………………… среднеквадратическое отклонение (σ)……………………………. ………………………………………………………………………….. (выпишите формулы и укажите, что характеризуют эти величины) |
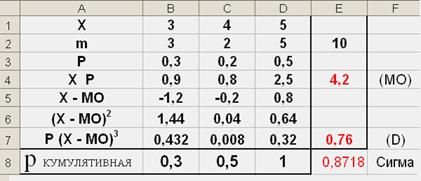
Составьте вариационный ряд для заданной таблицы распределения………………………………………………….???
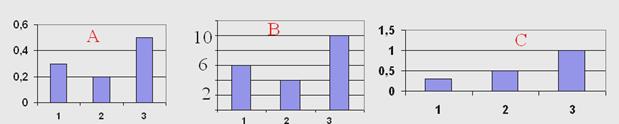
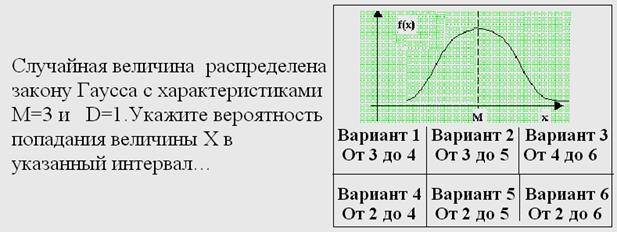
Поясните приведенные рисунки………………………….???
Непрерывные случайные величины
Сравнивая формулы М = Σ Xi * Pi, и M =-∞ ∫+∞ X*f(x)dx, укажите смысл функции распределения f(x )………..
…………………………………………………………………………
…………………………………………………………………………
Смысл функции f(x) состоит в том, что произведение f(x)dx указывает вероятность попадания случайной величины в интервал dx у значения x = xo.
Так как произведение f(x)dx -представляет собой дифференциал, то эта функция называется дифференциальной функцией распределения.
Проведите аналогию для формул дисперсии………………………..
D = Σ (Xi – Xср)2 * Pi, ……………………………………………….
D =-∞ ∫+∞(X – Xср)2*f(x)dx…………………………………………….
………………………………………………………………………….
σ = √ D ………………………………………………………???
Какой величиной можно считать пульс ?
……………………………………………………………………….
……………………………………………………………………….
| Основным теоретическим заключением данной темы является правила 1 сигма….. . . . . . . . . . . . . .. . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 2 сигма….. . . . . . . . . . . . . .. . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . 3 сигма….. . . . . . . . . . . . . .. . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . |  |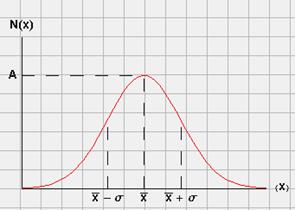
Если известно, что случайная величина подчиняется закону Гауса, то для нее можно сделать прогностические заключения следующего вида: С вероятностью р = 0,95 величина х будет попадать в интервал +/-2σ от математического ожидания х = а, то есть
Р (а - 2σ < x < а + 2σ) = 0,95
это правило двух сигма. Аналогично можно сделать прогностическое заключение для интервала +/- сигма и +/- три сигма. Доверительные вероятности при этом соответственно равны 0,68 и 0,9973.
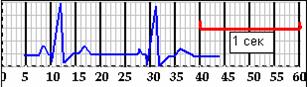Найдите мгновенную ЧСС по приведенной электрокардиограмме, измерив сначала длительность сердечного цикла …………………… ЧСС = ??? +/ ??? уд/мин.
Основы выборочного метода
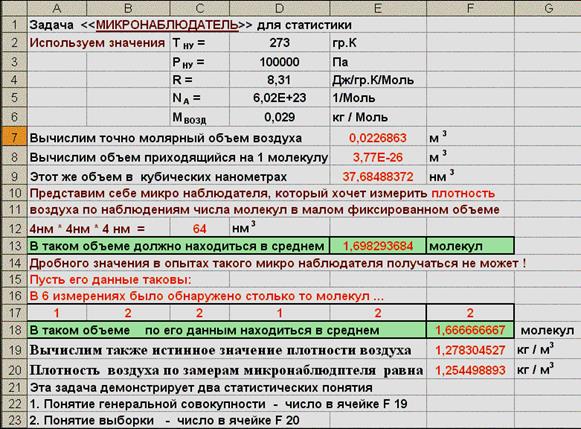
Понятие генеральной совокупности .....................................
Понятие выборки......................................................................
Понятие репрезентативности выборки..................................
Среднее значение (Xср) - оценка математического ожидания,
Выборочное среднеквадратическое отклонение (Sx) как оценка генерального значения среднеквадратического отклонения (σ).
Выборочная дисперсия обозначается как Sx2.
По каким формулам вычисляются среднее (Xср) и выборочное среднеквадратическое отклонение (Sx)
