Проверка статической значимости коэффициентов модели
Прежде всего, рассчитывается дисперсия в определении коэффициентов
Коэффициент считается значимым, когда его абсолютная вели чина больше доверительного интервала, т. е.
где t — критерий Стьюдента (берется из таблиц в зависимости oт уровня значимости а и числа степеней свободы при определении дисперсии опыта, табл. П2);
Sbj — среднеквадратичная ошибка определения коэффициентов
регрессии 
.
Смысл этого неравенства заключается в том, что абсолютная величина коэффициента должна быть в t раз больше, чем ошибка его определения.
Статическая незначимость коэффициента интерпретируется как отсутствие влияния соответствующего фактора в изученных интервалах его изменения. Такие коэффициенты из модели исключаются.
Проверка адекватности модели
Она необходима для того, чтобы ответить на вопрос — можно ли использовать полученное уравнение или необходима более сложная модель.
Адекватность модели проверяют с помощью критерии Фишера
где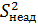 
– дисперсия неадекватности,
Здесь yiрасч , yiэксп — значения параметра оптимизации в i-м опыте, соответственно рассчитанные по уравнению регрессии и определенные экспериментально; k — число коэффициентов уравнения регрессии, включая b0 .
Гипотеза об адекватности уравнения принимается в том случае, когда рассчитанное значение F-критерия не превышает табличного для выбранного уровня значимости и числа степеней свободы f1, и f2, с которым определялись дисперсии неадекватности опыта (табл. ПЗ).
ОБОРУДОВАНИЕ, ИНСТРУМЕНТ, МАТЕРИАЛЫ
1. Вертикальный гидравлический пресс модели ПСУ-250.
2. Инструмент для прессования.
3. Заготовки из технически чистого свинца.
4. Штангенциркуль.
5. Масштабная линейка.
6. Ацетон, сухая ветошь.
7. Машинное масло, кисточка.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Выбрать независимые переменные изучаемого процесса по заданию преподавателя; определить центр эксперимента и область определения факторов; заполнить предлагаемую табл. 3.
Таблица 3
Выбор уровней факторов
| Уровни | Факторы | ||
| Основной | |||
| Интервал варьирования | |||
| Верхний | |||
| Нижний | |||
| Код | x1 | x2 | x3 |
2. Чтобы исключить влияние случайных ошибок, рекомендуется опыты, заданные матрицей планирования, проводить в случайной последовательности, т.е. рандомизированно по времени. Порядок проведения опытов следует выбирать по таблице случайных чисел (табл. Г14). Если, например, необходимо провести 4 опыта, то из любого места таблицы выписывают числа с 1 по 4, отбрасывал числа больше 4 и уже выписанные. Полученная последовательность цифр определяет последовательность проведения опытов и заносится в табл. 4 (столбцы 2, 3).
Таблица 4
Матрица планирования экспериментов
| № опыта | Порядок реализации опытов | x0 | x1 | x2 | x3 или x1,2 | Результаты эксперимента и дисперсии | Проверка адекватности модели | |||||
| n1 | n2 | y1 | y2 | yср |  | yi расч |  | |||||
| 1 2 3 4 | ||||||||||||
| Коэффициент bi | – | – | – |  | – | Σ |
3. В качестве силового оборудования для проведения экспериментов применяется вертикальный пресс ПСУ-250 усилием 2,5 мН. Заготовками для прессования служат полые цилиндрические слитки из свинца марки СО, размеры которых соответствуют размерам контейнера и применяемых игл.
Вытяжку меняют, используя иглы матрицы различных диаметров.
Прессование труб проводится на оснастке, показанной на рис. 1 и 2. Усилия прессования замеряются по шкале силоизмерителя, высота внутренних ребер на отпрессованных трубах определяется в трех сечениях со стороны выходного и утяжного концов, а также в середине трубы и с помощью штангенциркуля. Для выбора оптимальных геометрических размеров инструмента, обеспечивающих минимальную неравномерность истечения при прессовании ребристых изделий, целесообразно применять многоканальные матрицы, у которых совокупность каналов, расположенных на зеркале матрицы, можно рассматривать как трубу с наружным оребрением (рис. 2).
При прессовании в многоканальный инструмент происходит разделение металла в очаге деформации на отдельные потоки по соответствующим каналам. Объемы этих потоков по существу и определяют скорости истечения отдельных «ниток», длина которых не одинакова и зависит от геометрических параметров матриц и игл и технологических параметров процесса. Измерив длину участков lк с помощью масштабной линейки на любой стадии процесса, скорость истечения VK элемента К определяется как
где Фк – площадь к – го канала;
n – число элементов, на которые разделен канал ребристой трубы.
Оптимальные параметры игл рассчитываются из условия минимизации дисперсии скоростей истечения [2]
Рис. 1. Схема прессования трубы: α – без ребер, δ – с внутреннем оребрением.
Рис. 2. Схема прессования трубы с наружным оребрением.