Однофакторный дисперсионный анализ

Дисперсионным анализом называют статистический анализ результатов, зависящих от качественных факторов.

Сначала остановимся на случае одного фактора.

Пусть, например, ставится задача исследования влияния технологии обработки почвы на урожайность. Технологию естественно назвать фактором, а каждую конкретную технологию 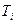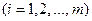— уровнем этого фактора. Здесь m— полное число применяемых технологий. Обозначим 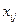— урожайность культуры, полученную в j-м году при использовании i -й технологии 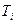( 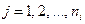, 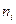— число лет, в течение которых производились наблюдения за применением технологии 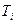). Сведем все данные в таблицу

				...
				...
				...
...	...	...	...	...	...
				...

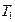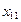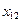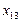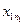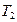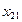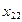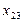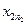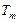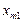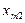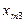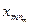В разных строчках этой таблицы содержится, вообще говоря, разное число элементов.

Рассмотрим математическую модель, в которой предполагается, что каждая случайная величина 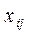может быть представлена в виде

,

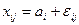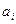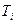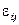где — урожайность, характерная для технологии , а — независимые случайные величины, которые описывают суммарный вклад всех случайных факторов, влияющих на итоговую урожайность. Чаще всего полагают, что все 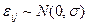, т.е. имеют нормальное распределение с нулевым математическим ожиданием и с одинаковой дисперсией .

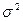Задача, которую предстоит решить, ставится следующим образом: выяснить, влияет ли выбор технологии обработки почвы на урожайность культуры или нет. На математическом языке это означает, что по результатам эксперимента необходимо проверить справедливость статистической гипотезы 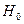о том, что все технологии 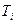одинаково эффективны, .

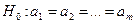Анализ результатов будет основан на сопоставлении двух оценок неизвестной дисперсии .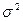

Одна из этих оценок не зависит от того, верна ли гипотеза 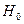. Для другой оценки это предположение существенно, т.е. эта оценка будет близка к значению 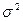только тогда, когда гипотеза 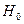верна.

Если обе оценки близки, то гипотезу 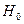следует принять. Если же оценки существенно отличаются, то гипотезу 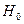следует отвергнуть.

Построим эти оценки.

Сначала для каждой строки вычислим средние

, ,

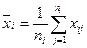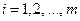а затем величину

.

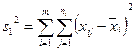Важно отметить, что при сделанных предположениях о случайных величинах 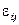, величина 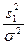имеет 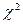- распределение с 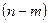степенями свободы независимо от того, верна ли гипотеза 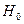. Следовательно, первая оценка для 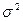получена.

Для получения второй оценки сначала вычислим величину

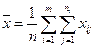, где ,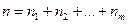

а затем вычислим

.

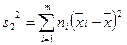При выполнении гипотезы 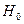величины 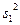и 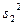независимы, а величина 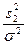имеет 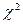- распределение с 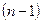степенями свободы.

Теперь сравним обе оценк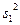и и 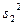. Если гипотеза 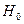верна, то величина

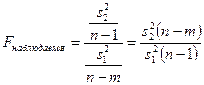
имеет распределение Фишера с 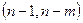степенями свободы. Напомним, что распределение Фишера характеризуется двумя параметрами: числом степеней свободы числителя и числом степеней свободы знаменателя.

Зададимся достаточно малым уровнем значимости 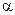и решим уравнение

.

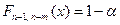Сравним корень этого уравнения 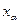с вычисленным выше значением .

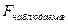При 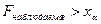гипотеза 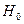отвергается. В противном случае — принимается.

Следующая задача — оценить степень влияния.

Для оценки степени влияния фактора используют выборочный коэффициент детерминации 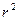, который вычисляется по формуле

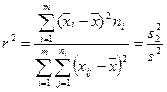, где

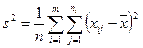— оценка полной выборочной дисперсии, .

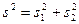Из 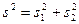видно, что полная выборочная дисперсия состоит из двух слагаемых, 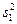и 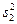, причем 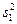— это средняя величина групповых дисперсий, а 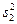— дисперсия групповых средних.

Величина 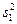характеризует изменчивость, обусловленную случайными факторами, а величина 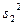определяет разброс средних значений в каждой группе около среднего значения всей выборки, т.е. зависит от различий параметров .

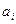Понятно, что коэффициент детерминации 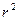показывает, какую часть в общей дисперсии величин 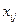составляет часть, обусловленная зависимостью от фактора .

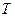Полученные результаты позволяют получить оценки параметров исходной модели.

Если гипотеза 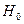принимается, т.е. 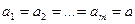, то оценкой параметра 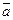(математического ожидания) является величина 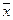, а оценкой дисперсии 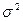является величина .

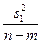Если же гипотеза 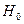отвергается, то оценкой 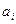является 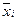, оценкой дисперсии 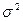для всех уровней является величина 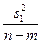, а эффект влияния i-го уровня можно вычислять по формуле .

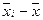Методика дисперсионного анализа основана на предположении о том, что величины 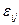, описывающие влияние случайных факторов имеют одинаковые групповые дисперсии .

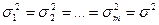Если уверенности в таком распределении 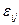нет, то прежде чем проводить дисперсионный анализ следует убедиться в том, что групповые дисперсии для всех уровней фактора совпадают.

На языке статистических гипотез это означает, что требуется убедиться в том, что гипотеза 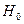об одинаковых групповых дисперсиях, 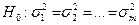, не противоречит результатам наблюдений.

Для этого вычислим несмещенные оценки групповых дисперсий

,

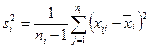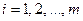
и величины

,

,

.

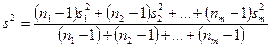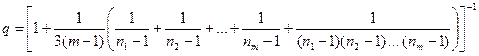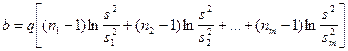Величина b называется критерием Бартлетта.

Доказано, что если гипотеза 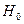верна и все 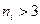, , 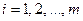то случайная величина b имеет распределение, близкое к 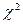-распределению с 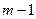степенями свободы.

Зададимся уровнем значимости 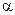и найдем правостороннюю критическую точку 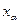— решение уравнения .

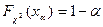Если 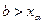, то гипотеза 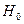отклоняется. В противном случае полагаем, что гипотеза не противоречит результатам наблюдений.

Пример. Выясним, на уровне значимости 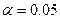, зависит ли урожайность сельскохозяйственной культуры от технологии обработки почвы по результатам, приведенным в таблице. Выясним также меру влияния каждой технологии, если это влияние подтвердится.

Номер технологии	Годы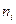

На приведенном ниже рисунке изображён фрагмент листа Excel c результатами вычислений.

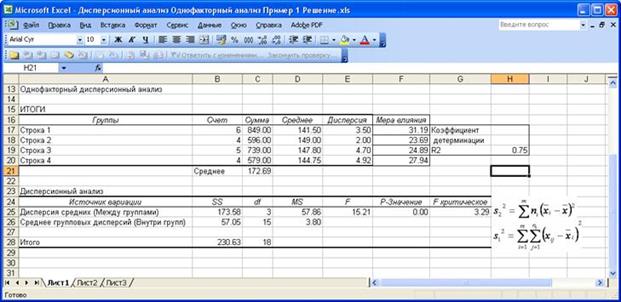
Выборочное значение критерия Фишера, F = 15.21, намного превышает критическое значение, равное 3.29.

Нулевая гипотеза о равенстве математических ожиданий для разных уровней фактора отклоняется.

С доверительной вероятностью 0.95, принимаем альтернативу – математические ожидания различны.

Таким образом, изменчивость урожайности объясняется, в числе, возможно других факторов, изменением технологии обработки почвы.