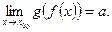Бесконечно малые и бесконечно большие функции.

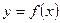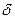Функция называется бесконечно большой при ,если для любого числа M>0 существует число = (М)>0, что для всех х, удовлетворяющих неравенству 0< 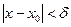, выполняется неравенство 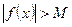. Записывают 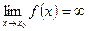. Коротко:

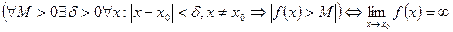
Функция 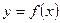называется бесконечно большой при 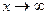,если для любого числа M>0 найдется такое число N=N (М)>0, что для всех х, удовлетворяющих неравенству 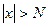, выполняется неравенство 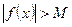. Коротко:

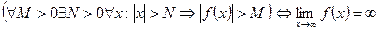
Всякая бесконечно большая функция в окрестности точки х0 является неограниченной в этой окрестности.

Бесконечно малая функция:
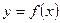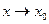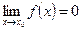Функция называется бесконечно малой при ,если : для любого числа 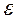>0 найдется число 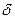>0 такое, что для всех х, удовлетворяющих неравенству 0< 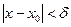, выполняется неравенство .

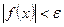Теорема: алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

Док-во:

Теорема: произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.

Док-во:

Следствие: так как всякая б.м.ф. ограничена, то из теоремы вытекает произведение двух б.м.ф. есть функция бесконечно малая.

Следствие: произведение б.м.ф. на число есть функция бесконечно малая.

Теорема: частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.

Док-во:

Теорема: если функция - бесконечно малая, то обратная ей функция – бесконечно большая и наоборот.

Док-во:

Односторонние пределы.

число А называется пределом функции 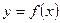слева в точке x₀, если для любого число 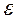>0 существует число 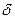= 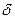( 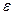)>0 такое, что при 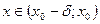выполняется неравенство .

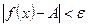Предел слева записывают так: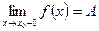

Аналогично определяется предел функции справа:

.

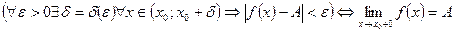Пределы функции слева и справа называются односторонними пределами.

Сравнение бесконечно малых.

Две б.м.ф. сравниваются между собой с помощью их отношения:

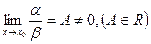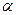1. если , то и 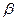называются бесконечно малыми одного порядка.

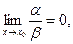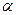2. если то называется бесконечно малой более высокого порядка, чем .

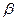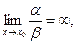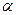3. если то называется бесконечно малой более низкого порядка, чем .

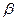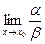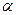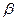4. если не существует, то и называются несравнимыми бесконечно малыми.

Таковы же правила сравнения б.м.ф. пр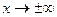и и .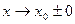

Эквивалентные бесконечно малые:

Sinx	x, при	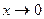ex - 1	x,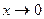
tgx	x,	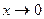ax - 1	x*lna,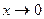
arcsinx	x,	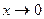ln(1+x)	x,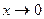
arctgx	x,	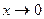loga(1+x)	x*logae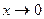
1-cosx	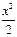,	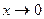(1+x)k - 1	k*x, k>0,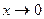

Теоремы о пределах.

Теорема: если существует 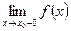и 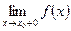и они равны между собой, то существует = .

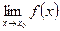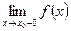
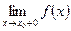Теорема: если 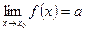, , 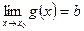то =>

1)

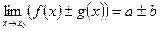
2)

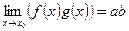
3)

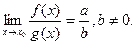
Примечание 1: 1-е и 2-е свойства распространяются на любое конечное число слагаемых или сомножителей, однако число слагаемых и сомножителей не может быть .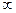

Примечание 2: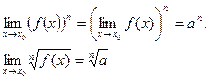

Теорема: если 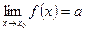, то функция g(x) = f(x) – a является б.м. при .

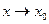Следствие: если 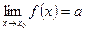=> в окрестности т. х₀ g(x) + а = f(x), где g(x)- б.м. при .

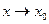Теорема: если 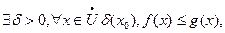и существуют конечные пределы, когда , => .

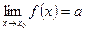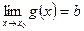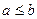Теорема (о сжатой переменной): если 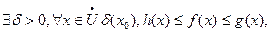и существуют конечные пределы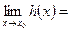 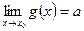=> существует: .

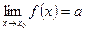Теорема (о пределе сложной функции):

Пусть: х_0, 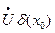, U=f(x), .

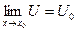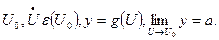
Сама теорема:

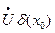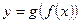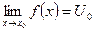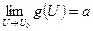Если задана сложная функция, и существуют конечные пределы и , то