Замечательные пределы. Сравнение бесконечно малых величин
В приведенных выше примерах нам было достаточно несложных алгебраических преобразований для получения ответа. Иная ситуация возникает, если выражение содержит трансцендентные функции, типа синуса, логарифма и другие. В этом случае нам помогут некоторые пределы, называемые в математике «замечательными» пределами и сравнение бесконечно малых величин между собой.
Первый замечательный предел: 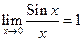 ,
,
Второй замечательный предел: 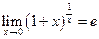 , или
, или 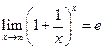 ,
, 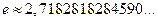 - иррациональное число.
- иррациональное число.
Сравнение бесконечно малых величин между собой определяется через предел их отношения. Пусть 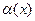 и
и 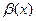 бесконечно малые величины при
бесконечно малые величины при 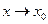 . Правила сравнения запишем в таблицу:
. Правила сравнения запишем в таблицу:
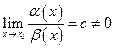 | Величины одного порядка малости | |
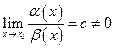 | Эквивалентные величины | 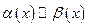 . Читается: . Читается: 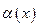 эквивалентно эквивалентно 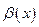 при при 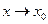 . . |
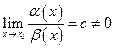 | Величина 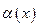 имеет больший порядок малости по сравнению с величиной имеет больший порядок малости по сравнению с величиной 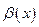 | 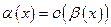 . Читается: . Читается: 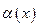 есть есть 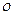 - малое по сравнению с - малое по сравнению с 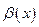 при при 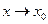 . . |
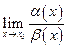 не существует не существует | Величины не сравнимы между собой |
На основании замечательных пределов можно получить таблицу эквивалентных величин при 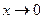 .
.
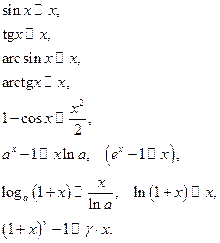
Заметим, что слева в формулах стоят различные функции, а сравниваются все они со степенной функцией, наиболее простой для работы.
Примеры сравнений:
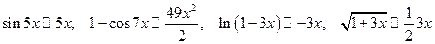 .
.
Теорема.Пустьпри 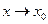
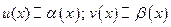 . Тогда справедливы равенства:
. Тогда справедливы равенства:
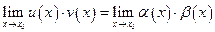 ,
, 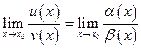 . ●
. ●
Примеры на вычисление пределов с использованием таблицы эквивалентных величин:
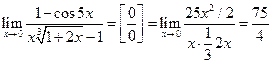 ,
, 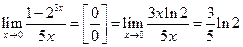 .
.
Если при вычислении пределов с неопределенностью 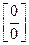 переменная стремится к числу, отличному от нуля, то для возможности использовать таблицу, сначала необходимо сделать замену переменной. Например:
переменная стремится к числу, отличному от нуля, то для возможности использовать таблицу, сначала необходимо сделать замену переменной. Например:
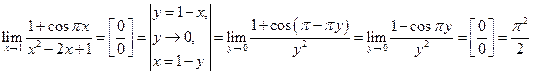 .
.
Пояснения к решению примера. Подставив предельное значение в заданный пример, получили неопределенность вида 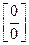 , т.е. отношение бесконечно малых величин. Но таблицей воспользоваться нельзя, так как таблица справедлива только для случая, если переменная стремится к нулю. Сделаем замену переменной (замена выделена вертикальными линиями) и преобразуем выражение. Подставив новую переменную в выражение для предела, снова получаем неопределенность
, т.е. отношение бесконечно малых величин. Но таблицей воспользоваться нельзя, так как таблица справедлива только для случая, если переменная стремится к нулю. Сделаем замену переменной (замена выделена вертикальными линиями) и преобразуем выражение. Подставив новую переменную в выражение для предела, снова получаем неопределенность 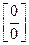 , но теперь мы уже могли воспользоваться таблицей эквивалентных величин, что и было сделано.
, но теперь мы уже могли воспользоваться таблицей эквивалентных величин, что и было сделано.
Вычисление пределов при неопределенности 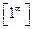 . Можно предложить несколько способов. Рассмотрим пример: вычислить
. Можно предложить несколько способов. Рассмотрим пример: вычислить 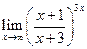 . Непосредственная подстановка предельного значения приводит к неопределенности
. Непосредственная подстановка предельного значения приводит к неопределенности 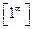 .
.
Первый способ – логарифмировать заданное выражение. Обозначив заданную функцию 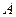 , получаем
, получаем
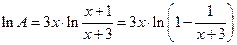 ,
,
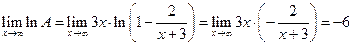 .
.
Следовательно, 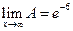 .
.
Второй способ ─ построение выражения в виде 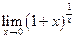 :
:
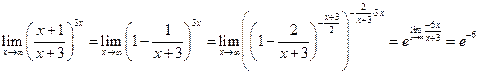 .
.
Производная функции
Пусть функция 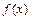 определена в точке
определена в точке 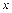 и ее окрестности. Если существует конечный предел
и ее окрестности. Если существует конечный предел
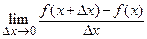 , (3)
, (3)
то этот предел называется производной функции в точке 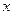 и обозначается
и обозначается 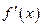 или
или 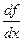 .
.
При существовании односторонних пределов 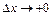 или
или 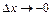 говорят о существовании односторонних производных.
говорят о существовании односторонних производных.
Функция, имеющая в каждой точке промежутка конечную производную, называется дифференцируемой функцией на этом промежутке.
Вычисляется производная с использованием таблицы производных и согласно правилам дифференцировании.
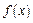 | 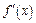 | Правила дифференцирования |
| const | I. 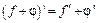 . II. . II. 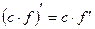 . III. . III. 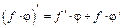 . IV. . IV. 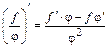 . V. . V. 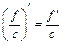 . VI. . VI. 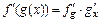 (дифференцирование сложной функции)/ VII. (дифференцирование сложной функции)/ VII. 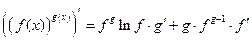 . АЛГОРИТМ вычисления производных: · Найти последнее действие (функцию). · Применить формулы I–V. · Применить таблицу производных. Замечание. Выражения . АЛГОРИТМ вычисления производных: · Найти последнее действие (функцию). · Применить формулы I–V. · Применить таблицу производных. Замечание. Выражения 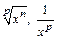 , , 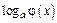 следует предварительно преобразовать по формулам: следует предварительно преобразовать по формулам: 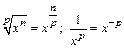 ; ; 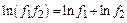 ; ; 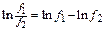 ; ; 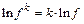 | |
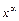 | 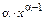 | |
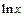 | 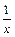 | |
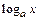 | 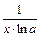 | |
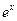 | 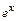 | |
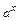 | 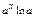 | |
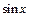 | 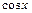 | |
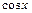 | 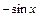 | |
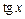 | 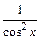 | |
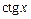 | 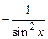 | |
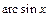 | 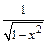 | |
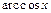 | 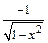 | |
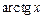 | 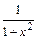 | |
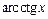 | 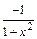 |
Производная от первой производной называется второй производной или производной второго порядка и обозначается 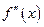 или
или 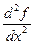 . Аналогично определяются производные более высоких порядков.
. Аналогично определяются производные более высоких порядков.
Геометрический смысл производной. Пусть функция непрерывна на промежутке в окрестности точки 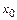 , а график функции имеет в этой точке касательную, не параллельную оси
, а график функции имеет в этой точке касательную, не параллельную оси 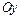 . Тогда
. Тогда
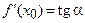 , (4)
, (4)
где 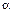 – угол между положительным направлением оси
– угол между положительным направлением оси 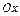 и касательной (рис. 1).
и касательной (рис. 1).
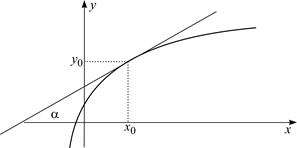
Рис. 1
Уравнение касательной к графику функции в точке 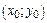 имеет вид
имеет вид
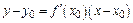 . (5)
. (5)
Пример 3.Найти производную функции 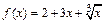 в точке
в точке 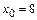 .
.
Решение. 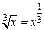 .
. 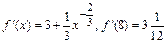 .
.
Пример 4.Найти производную функции 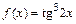 в точке
в точке 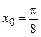 .
.
Решение. Заданная функция – сложная. Используем формулу дифференцирования сложной функции.
Тогда 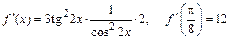 .
.
Правило Лопиталя
Теорема.Пусть функции 1) 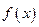 и
и 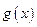 определены в окрестности точки
определены в окрестности точки 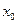 и существуют конечные производные, 2)
и существуют конечные производные, 2) 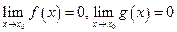 , 3) существуют конечные производные
, 3) существуют конечные производные 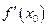 и
и 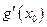 , причем
, причем 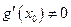 , 4) существует предел
, 4) существует предел 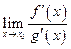 , Тогда
, Тогда
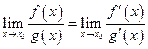 . ●
. ●
Здесь приведена одна из теорем Лопиталя. Аналогичное правило вычисления предела справедливо д с неопределенностью 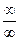 .
.
Примеры вычисления пределов с помощью правила Лопиталя:
1.  ,
,
2. 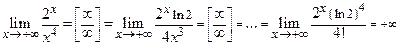 ,
,
3. 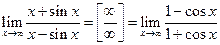 .
.
Во втором примере мы применили правило Лопиталя 4 раза. В третьем примере правило Лопиталя не применимо, так как не существует предела производных. Нет лекарства от всех бед. Предел же легко вычисляется с использованием теорем и равен единице.
Рекомендуем запомнить пределы:
, .
