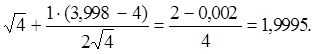Тема 3.дифференциальное исчисление
| Элементы содержания | Требования к знаниям и умениям |
| Правила дифференцирования | знать: основные правила и формулы дифференцирования уметь: применять основные правила и формулы дифференцирования при решении задач |
| Производная сложной функции | знать: правило нахождения производной сложной функции уметь: находить производные сложных функций |
| Производная функции в точке | знать: основные правила и формулы дифференцирования уметь: находить производные функций и их значения в точке |
| Экстремум функции | знать: правило отыскания экстремумов функции уметь: находить точки экстремумов функции и экстремумы функции |
| Наибольшее и наименьшее значения функции | знать: правило нахождения наибольшего и наименьшего значений функции уметь: находить наибольшее и наименьшее значения функции |
| Дифференциал функции | знать: понятие дифференциала уметь: применять дифференциал для нахождения приближенного значения функции |
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Понятие производной
Определение: Производной функции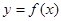 
по аргументу x называется предел отношения ее приращения 
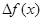к приращению 
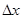аргумента x, когда приращение аргумента стремится к нулю:
.
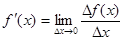Если этот предел конечный, то функция y=f(x) называется дифференцируемой в точке x. Если же этотпредел есть ∞, то говорят, что функция y=f(x) имеет в точке x бесконечную производную.
Механический смысл производной:скорость есть первая производная пути по времени, т.е.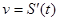 
.
Геометрический смысл производной:тангенс угла наклона касательной к графику функции 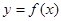равен первой производной этой функции , вычисленной в точке касания, т.е.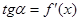 
Уравнение касательнойк графику функции 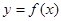в точке 
:
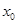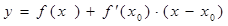
Уравнение нормали к графику функции 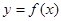в точке :
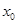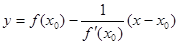
Таблица производных
           |          |
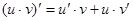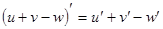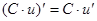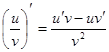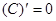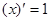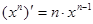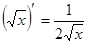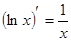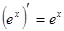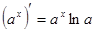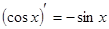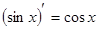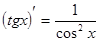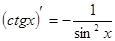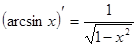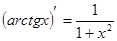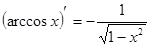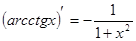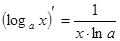Процесс нахождения производных называется дифференцированием функции.
Рассмотрим примеры.
Найти производные функций:
Пример 1: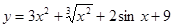 
Решение: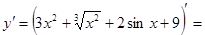 
+
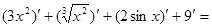
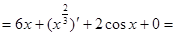
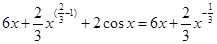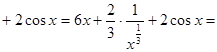
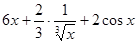
Пример2: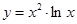 
Решение: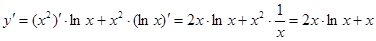 
Пример 3: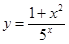 
Решение: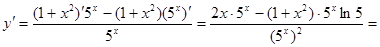 
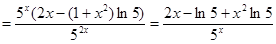
Дифференциал функции
Определение: Дифференциалом функции y=y(x) называется произведение ее производной на дифференциал независимой переменной:
.
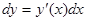Для большей наглядности рассмотрим пример.
Пример 1: Найти дифференциал функции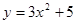 
Решение: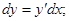 
Так как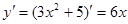 
, то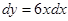 
.
Для дифференцируемой в точке х0 функции f(x), у которой f¢(x0) ¹ 0, при достаточно малых ∆х справедливо приближенное равенство
∆f(x0) ~ df(x0) = f¢(x0)∆x
Т.к. ∆х = х – х0, ∆f(x0) = f(x0 + ∆x) – f(x0) = f(x) – f(x0),
то f(x) ~ f(x0) + f¢(x0) (x–x0)
Например, вычислим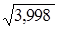 
.
Рассмотрим функцию f(x) =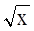 
, х Î (0; +¥).
Для этой функции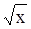 
~ 
+ 
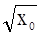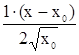
Подставляем х = 3,998 и х0= 4
~ 
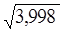