Теорема Самарского о сходимости стационарных методов
Теорема. Пусть  ,
,  и
и  , тогда итерационный процесс
, тогда итерационный процесс
 (3.15)
(3.15)
сходится при любом выборе начального приближения  .
.
Метод Якоби
Представим матрицу A в виде суммы трех матриц  , где
, где
 - нижняя треугольная матрица с 0 на главной диагонали.
- нижняя треугольная матрица с 0 на главной диагонали.
 - верхняя треугольная матрица с 0 на главной диагонали.
- верхняя треугольная матрица с 0 на главной диагонали.
 .
.
Для метода Якоби имеем  и
и  :
:
 .
.
 . (3.16)
. (3.16)
Запишем метод в координатной форме:
 для всех
для всех 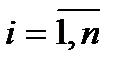 .
.
 для всех
для всех 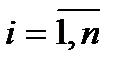 .
.
Предполагается, что  для всех
для всех 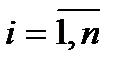 .
.
Алгоритм метода Якоби
· Задание исходных матрицы A и вектора правой части f.
· Проверка выполнения условия  для всех
для всех 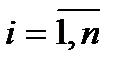 .
.
· Задание начального приближения  .
.
Строго говоря, задавать любое начальное приближение для любого итерационного метода нельзя. При формулировке любого итерационного метода обычно оговариваются условия выбора  . Если этих условий нет, то часто берут
. Если этих условий нет, то часто берут  или
или  . От выбора
. От выбора  зависит скорость сходимости метода, поэтому иногда прибегают к подбору.
зависит скорость сходимости метода, поэтому иногда прибегают к подбору.
· Выполнение следующей итерации  . Вычисление очередного приближения
. Вычисление очередного приближения 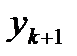 .
.
· Проверка условия сходимости. Обычно используют критерий  , где
, где  - норма.
- норма.
· В случае выполнения условия - печать решения и невязки, количества выполненных итераций.
Возможные ошибки
· Плохое начальное приближение.
· Ошибки при организации суммирования.
· Замена в формулах известного приближения 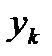 на искомое
на искомое 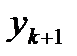 .
.
· Ошибка с индексами переменных.
· Неправильно переписанная формула метода.
· Ошибка в критерии условия сходимости.
Теорема сходимости метода Якоби
Теорема. Пусть  с диагональным преобладанием, тогда метод Якоби сходится для любого начального приближения.
с диагональным преобладанием, тогда метод Якоби сходится для любого начального приближения.
Рекомендации
· Если задача не подходит под условие теоремы, то это еще не значит, что метод нельзя использовать.
· При составлении программы рекомендуется придумать новую вспомогательную задачу с матрицей  с диагональным преобладанием, решение для которой заранее известно. Отладив программу для вспомогательной задачи, приступайте к решению своей конкретной задачи.
с диагональным преобладанием, решение для которой заранее известно. Отладив программу для вспомогательной задачи, приступайте к решению своей конкретной задачи.
· На практике проверить достаточные условия сходимости бывает довольно трудно или невозможно. Поэтому часто метод и его параметры подбирают эмпирически.
Метод Зейделя
Для метода Зейделя берут  и
и  :
:
 .
.
 . (3.17)
. (3.17)
Запишем метод в координатной форме:
 для всех
для всех 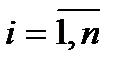 .
.
Теорема сходимости метода Зейделя
Теорема. Пусть  , тогда метод Зейделя сходится для любого начального приближения.
, тогда метод Зейделя сходится для любого начального приближения.
Метод верхней релаксации
Положим  и
и  - параметр >0:
- параметр >0:
 .
.
 (3.18)
(3.18)
Запишем метод в координатной форме:
 для
для 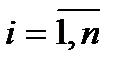 .
.
Итак,
 .
.
 ,
,
и т.д.
Теорема сходимости метода верхней релаксации
Теорема. Пусть  и
и  , тогда метод верхней релаксации сходится для любого начального приближения.
, тогда метод верхней релаксации сходится для любого начального приближения.
Метод итерации
Решаем систему уравнений  . Предполагаем, что
. Предполагаем, что  для всех
для всех 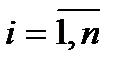 .
.
Разрешим первое уравнение системы относительно  , второе уравнение относительно
, второе уравнение относительно  и т.д. В результате получим следующую систему уравнений:
и т.д. В результате получим следующую систему уравнений:
 , (3.19)
, (3.19)
где  ,
,  при
при  и
и  при
при 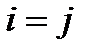 .
.
Следовательно, систему (3.19) можно записать в виде  .
.
