Независимые испытания. Формула Бернулли
При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли.
Примеры повторных испытаний:
1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну;
2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой (роль пристрелки не учитывается).
Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы; вероятность появления события А в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события А в единичном испытании буквой р, т.е.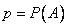 
, а вероятность противоположного события (событие А не наступило) - буквой 
.
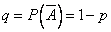Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражаетсяформулой Бернулли
Распределение числа успехов (появлений события) носит название биномиального распределения.
Пример. В урне 20 белых и 10 черных шаров. Вынули 4 шара, причем каждый вынутый шар возвращают в урну перед извлечением следующего и шары в урне перемешивают. Найти вероятность того, что из четырех вынутых шаров окажется 2 белых.
Решение. Событие А – достали белый шар. Тогда вероятности
, 
.
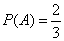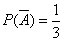По формуле Бернулли требуемая вероятность равна
.
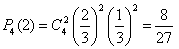Пример. Определить вероятность того, что в семье, имеющей 5 деталей, будет не больше трех девочек. Вероятности рождения мальчика и девочки предполагаются одинаковыми.
Решение. Вероятность рождения девочки
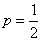, тогда 
.
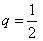Найдем вероятности того, что в семье нет девочек, родилась одна, две или три девочки:
, 
,
, 
.
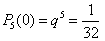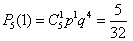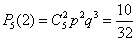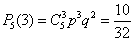Следовательно, искомая вероятность
.
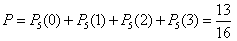Пример. Среди деталей, обрабатываемых рабочим, бывает в среднем 4% нестандартных. Найти вероятность того, что среди взятых на испытание 30 деталей две будут нестандартными.
Решение. Здесь опыт заключается в проверке каждой из 30 деталей на качество. Событие А - «появление нестандартной детали», его вероятность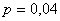 
, тогда 
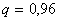. Отсюда по формуле Бернулли находим
.
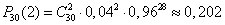Пример. При каждом отдельном выстреле из орудия вероятность поражения цели равна 0,9. Найти вероятность того, что из 20 выстрелов число удачных будет не менее 16 и не более 19.
Решение. Вычисляем по формуле Бернулли:
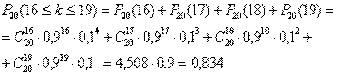
Пример. Независимые испытания продолжаются до тех пор, пока событие А не произойдет k раз. Найти вероятность того, что потребуется n испытаний (n ³ k), если в каждом из них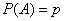 
.
Решение. Событие В – ровно n испытаний до k-го появления события А – есть произведение двух следующий событий:
D – в n-ом испытании А произошло;
С – в первых (n–1)-ом испытаниях А появилось (к-1) раз.
Теорема умножения и формула Бернулли дают требуемую вероятность:
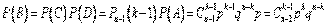
Надо заметить, что использование биномиального закона зачастую связано с вычислительными трудностями. Поэтому с возрастанием значений n и m становится целесообразным применение приближенных формул (Пуассона, Муавра-Лапласа), которые будут рассмотрены в следующих разделах.