Повторные независимые испытания. Формула Бернулли

Опыты наз-ся независимыми,если при каждом из них событие А наступает с одной и той же вер-тью Р(А)=р, независящий от того появилась или не появилась в др испытаниях. При этом вер-ть противоположного события Р(Ā)=q,причем p+q=1.

Пусть произ-ся испытание,в каждом из которых может появится событие А или Ā.Вер-ть события А появ-ся в серии из n-независимых испытаний ровно m раз(m≤n)может быть вычислено по формуле Бернулли:

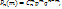
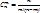
11. Наивероятнейшее число появлений события в схеме Бернулли.Число наступлений m₀ события А называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события А любое другое количество раз. Наивероятнейшее число наступлений события А в n испытаниях заключено между числами np-q и np+p : np-q≤m₀≤np+p. Если np-q – целое число, то наивероятнейших чисел 2: np-q и np+p.

12. Локальная и интегральная теоремы Лапласа. Локальная.Если вер-ть наступл-я соб-я А в кажд. из n незав. испыт-й =одной и той же пост величине(n>10), причем p(o<р<1), а n велико, то вер-ть Рn(m) того, что в этих испытаниях соб-е А наступит ровно m раз выч-ся по ф-ле: Pn(m)= (1/√npq)*φ(x), где x=m-np/√npq, φ(x)=(1/√2π)*e-x2/2 ; замечания:φ(-x)=φ(x), для х>5 φ(x)=0. Интегральная.Если вер-ть наступл-я соб-я А в кажд. из n незав-х испыт-й =р, причем o<р<1, а n велико, то вер-ть того, что событие А в этих испыт-х наступит m раз, причем m1<m<m2, м. найти: Рn(m1<m<m2)=(0.5)(Φ(x2)-Φ(x1), где x1=m1-np/√npq, x2=m2-np/√npq, Ф(x) –ф-ция Лапласа=(1/√2π)∫x0℮-t в квадрате/2dt. Применяют если npq>9. Св-ва ф-ции: Ф(x)= -Ф(x), Ф(х) – возраст-т на R, для х>5 Ф(х)=0,5.

13. Формула Пуассона для редких событий.Ф-ла Pn(m)=(1/√npq) φ ((m-np)/√npq) (1)позволяет получать тем более близкие к точному значения Pn(m) результаты, чем больше знач. корня √npq и чем ближе знач . p и q к ½.Если в-сть успеха р по отдельным испытаниям близка к 0 (такие события наз. редкими), то даже при большом n, но малом np (np<10) в-сти, полученные по ф-ле (1) недостаточно близки к их истинным знач. В этом случае прим. другую асимптотическую ф-лу – ф-лу Пуассона. Теорема: Если в-сть наступления события А в каждом из независимых испытаний постоянна, но близка к 0, а np=λ<10, то n(m)≈λm(e-λ/m!) Замечание: ф-лу Пуассона исп., когда n≥10 (n≥100), а np≤10.

14. Дискретная случайная величина, ее закон распределения. Многоугольник распределения.Случ.вел. – переменная вел., к-рая в зав-ти от исхода опыта принимает значения, в зав-ти от случая. ДСВ – случ.вел., приним. разл. значения, к-рые м. записать в виде кон. или беск. посл. чисел. НСВ – случ.вел., к-рая м. принимать все знач-я из нек-рого промежутка. З-н распр. ДСВ – соответствие м-ду знач-ми х1, х2, х3… этой вел. и их вер-тями р1, р2, р3… Если ДСВ Х приним. конечное множ-во знач-й х1, х2…хn с вер-тями р1, р2…рn, то ее з-н распределения опред-ся: Р(Х=хk)=Pk, k=1,n (При этом ΣРk=1). М. задать табличкой:

х	х1	х2	…	хn
р	р1	р2	…	рn

Ряд распр-я ДСВ можно изобразить графически в виде полигона или многоугольника распр-я вер-стей. Для этого по горизонт. оси в выбранном масштабе нужно отложить знач-я СВ, а по вертик. – в-сти этих знач-й, тогда точки с корд-тами (x_i , p_i ) будут изображать полигон распр-я в-стей. Соединив же эти точки отрезками прямой, получим многоуг-к распр-я в-стей.

15. Функция распределения вероятностей случайной величины и ее свойства.Функцией распределения случайной величины Х называется функция FX(x)= P{X<x}, xÎR. Под {X<x}понимается событие, состоящее в том, что случайная величина Х принимает значение меньшее, чем число х. Если известно, о какой случайной величине идёт речь, то индекс, обозначающий эту случайную величину, опускается: F(x) º FX(x). Как числовая функция от числового аргумента х, функция распределения F(x) произвольной случайной величины Х обладает следующими свойствами:1)для любого xÎR: 0£ F(x) £ 1. 2) F(-¥) = limx®¥ F(x) = 0 ; F(+¥) = limx®¥ F(x) = 1;3) F(x)-неубывающая функция, т.е.для любых α,βтаких, что α< β :F(β) - F(α);4)непрерывна слева

16. Математическое ожидание дискретной случайной величины и его свойства.Мат. ожидание ДСВ Х, принимающее конечное множество значений с законом распределения P(x=xk)=Pk 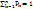вычисляется по формуле: M(x)= 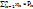или M(x)=x1P1+x2P2+….+xnPn Математическое ожидание дискретной случайной величины ≈ среднему арифметическому всех значений этой случайной величины. Свойства M(x): 1. a≤M(x)≤b, где a – наименьшее, b – наибольшее значение случайной величины X. 2. M(C)=C, где C=const. 3. M(Cx)=C*M(x) 4. M(X≠Y)=M(X)≠M(Y) 5. M(xy)=M(x)*M(y)

17. Дисперсия дискретной случайной величины и ее свойства. Среднее квадратическое отклонение. На практике часто требуется оценить рассеяние возм. знач-й случ. вел-ны вокруг ее среднего значения. Дисперсией (рассеиванием) лучайной величины X называется математическое ожидание квадрата ее отклонения от ее мат. ожидания, т.е. D(X)=M(X-M(X))² или D(X)=M(X²)-(M(X))² Свойства: 1. D(X)≥0 2. D(C)=0 3. D(CX)=C²D(X) 4. D(X±Y)=D(X)±D(Y) Ср.квадратич. отклонением СВ Х наз-ся величина σ (Х)= корень квадр. из D(X)

Среднее квадр. откл-е характ. степень откл-я СВ от ее мат. ожид-я и имеет размерность знач-й СВ.

18. Биномиальный закон распределения и его числовые характеристики. Пусть проводится n независимых испытаний. В результате каждого из которых возможны 2 исхода: А – успех с вероятностью p, или 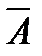- неуспех с вероятностью q = 1-p. Тогда вероятность числа m успех 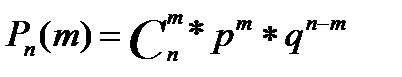Дискретная случайная величина X, которая может принимать только целые неотрицательные значения с вероятностями P (X=m)= 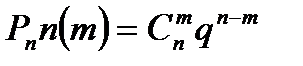, где p>0, q>0, m 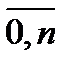0,n называется распределенной по биноминальному закону с параметром p. Мат.ожидание M(X)= np Дисперсия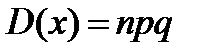 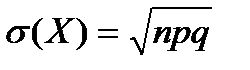- среднее квадратическое отклонение.

19. Геометрическое распределение.Геометрическим распределением называется распределение ДСВ X, определяемое формулой P(X=m)=q^(m-1)*p, 0<p<1, m=1, 2, 3…Вероятности образуют бесконечно убывающую геометрическую прогрессию со знаменателем q=1-p (с этим связано название). Мат. ожидание равно M(x)= Дисперсия равна D(x)= 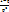20. Гипергеометрическое распределение.Пусть имеется N элементов, из кот-х М эл-тов облад. некот-м признаком А. извлек. случ. образом без возвращ-я n эл-тов. X – ДСВ, число эл-тов, облад. признаком А, среди отобр. n эл-тов. В-сть, что Х =m опред. по формуле: P(x=m)= Мат. ожидание и дисперсия СВ, распред. по гипергеом. закону, опред. формулами: M(x)=n* , D(x)=n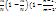

21. Формула Пуассона. Распределение Пуассона.Если число испытаний велико, а вер-сть появл-я события в каждом испытании очень мала, то используют приближенную формулу Пуассона: 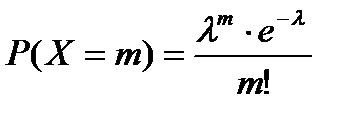,где λ=np (среднее число появл-я события в n испытаниях), m – число появления события в n независимых испытаниях; m приним. значения 0,1,2,…,n. Мат. ожидание и дисперсия СВ, распределенной по закону Пуассона, совпадают и равны параметру λ : M(X)=λ, D(X)=λ, Т.к. для распред. Пуассона вер-ть появления события в каждом испытании мала, то его еще назыв. з-н распред. редких явлений.

22. Непрерывная случайная величина, плотность распределения вероятностей непрерывной случайной величины и ее свойства.Случ. вел-на Х наз. непрерывной, если ее функция распред-я непрерывна в любой точке и дифференцируема всюду, кроме отдельных точек. Теорема. Вероятность любого отдельного знач-я непрер. случ. вел-ны равна нулю: P(X=x₁)=0. Для НСВ P(x₁< X < x₂)=F(x₂)-F(x₁). Ф-ция распред.опис.как ДСВ, так и непрерыв.СВ,однако,такой способ задания неперыв.СВ не единств.Их удобно описывать ф-цией,кот. наз. плотностью распред.вероят.или дифференц.ф-цией.(Р(Х)-дифференц.ф-ция плотность интегральная). Плотностью распред. вероят.непрерыв. СВ X наз. ф-ция р(х),кот. равна первой производной от ф-ции распред.Р(Х),т.е р(х)=F’(х). Свойства: 1.(вместо f – p) 1.f(x)≥0 для люб.x – cв-во неотриц-ти.2. 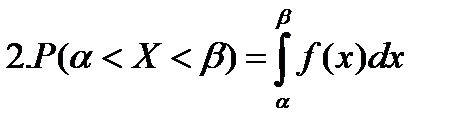3. 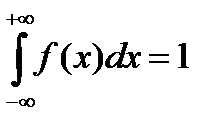- Cв-во нормировки.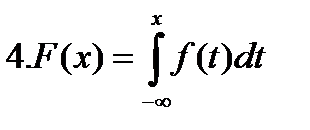

23. Математическое ожидание и дисперсия непрерывной случайной величины Мат.ожид.НСВ Х, все знач., кот. х принадлежит[альфа,бета] с плотностью вероят.р(х), вычисл. по формуле: 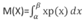Если НСВ X определена на(-00;+°°),то мат.ожид. опред. по формуле 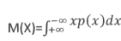(требуется абсолют.сходимость интеграла.)

Дисперсия НСВ, X принадлежит интервалу (альфа, бета) с плотностью р(Х) вычисл.по формуле: 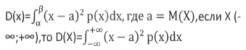(абсолют.сходимость интеграла требуется)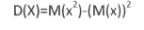

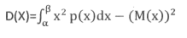
24. Равномерный закон распределения и его числовые характеристикиНепр. случ. велич.х распред. равномерно на отрезке [а;b], если её плотность вероятности р(х) постоянна на этом отрезке и =0 вне его:

Р(х)= {1/ (b-a), при а< =х<=b, О, при х<а, х>b

Функция распред. случайн. величины, распред-ой по равномерн. закону, имеет вид:

F(x)= { O, x<=a, (x-a)/(b-a), a<x<=b, 1, x>b

Мат. ожидание, дисперсия, средн. кв. откл-е:МХ=(а+b)/2; DХ=(b-а)( b-a)/ 12

25. Показательный закон распределения и его числовые характеристики.Непрерывная СВ Х имеет показ. (экспоненциальное) распределение с параметром λ >0, если ее плотность распред-я имеет вид: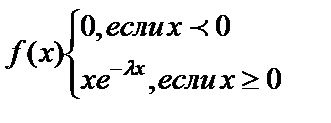

Ф-ция распределения СВ, распределенной по показ. з-ну: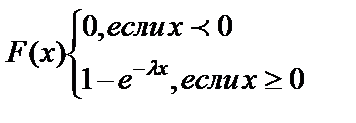

Показательному распределению обычно подчиняется величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств, другими словами – величина промежутка времени между появлениями двух послед-х редких событий. Вероятность попадания случайной величины Х на интервал (α;β)

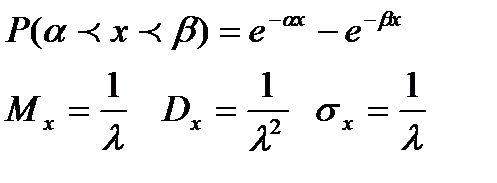
Рис. 3.6. Вид кривой распределения при разных значениях s: s3<s2<s1 .

26. Нормальный закон распределения. Влияние параметров распределения на вид нормальной кривой. Непрерывная случайная величина X имеет нормальный закон распределения с параметрами а и 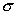, если её плотность вероятности f(x) имеет вид: 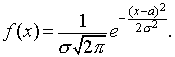Кривая нормального распределения f(x) (нормальная кривая или кривая Гаусса) приведена на рисунке.

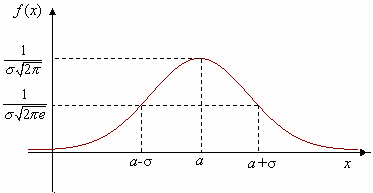График симметр. относит. а. При изменении параметра а форма кривой не меняется, а ее график сдвигается влево или вправо. При изменении параметра σ меняется форма нормальной кривой: с увеличением параметра σ кривая должна приближаться к 0Х и растягиваться вдоль этой оси, а с уменьшением σ кривая стягивается к прямой х=а.

27. Числовые характеристики случайной величины, имеющей нормальное распределение. Непрерывная случайная величина X имеет нормальный закон распределения с параметрами а и 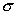, если её плотность вероятности f(x) имеет вид: 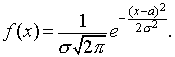Математическое ожидание случайной величины X, распределённой по нормальному закону, равно параметру а этого закона, а её дисперсия - квадрату параметра 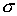, т.е. 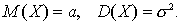Величина М(Х) называется также центром рассеяния, а среднеквадратичное отклонение 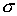характеризует ширину кривой распределения. С возрастанием 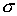максимальная ордината кривой убывает, а сама кривая становится более пологой, растягиваясь вдоль оси абсцисс, тогда как при уменьшении 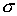кривая вытягивается вверх, одновременно сжимаясь с боков

28. В-сть попад-я в зад. интервал нормально распред. случ. в-ны. В-сть зад. откл-я. Правило трех сигм.В-сть попадания нормально распр. СВ Х в заданный интервал 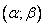опр. ф-лой 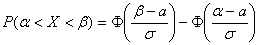.Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины Х от ее М(х) =а по абсол. величине меньше заданного полож. числа ε. 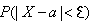; ; 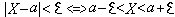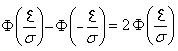При реш-и многих важных практич. задач делают предпол-е, что СВ распределена по норм. закону. Возн. вопрос, на каком основании делается такое допущение. Для иссл-я этого вопроса рассм. одну характ. особ-сть норм. распред-я СВ. Найдем в-сти событий: |x-a|<σ ;|x-a|<2σ ; |x-a|<3σ Используем формулу:P(|x-a|<σ)=2Ф(1)=0,6826 P(|x-a|<2σ)=2Ф(2)= 0,9594 P(|x-a|<3σ)=2Ф(3)=0,9973 – это событие практически достоверное.Заглянем в таблицу: Из последнего соотношения следует, что практически все возможные значения норм. распр-я СВ x принадлежат интервалу (a-3σ; a+3σ)

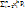29. Моменты случайной величины. Асимметрия. Эксцесс. Начальным моментом ν к СВ X называется математическое ожидание ее k-й степени, т.е. νк=M(xк).Для ДСВ Х, принимает значение X1, X2, …,Xn с вероятностью P1, P2, …Pn. νk= Для НСВ Х с p(x) начальный момент k-о порядка определяются по формуле:νk=M(xn)= 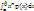; νk=M(xn)=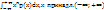 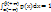- условие Центр. теорет. момент порядка k х μк= 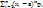Для непрер. СВ Х: μк= 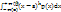Следствия: 1. ν0=1, μ0=1 2. ν1=M(x), μ1=0 3. ν2=M(x²), μ2=D(x), μ2= ν₂-ν₁² 4. μ3=v₃-3v₁v₂+2v₁³. Ассиметрией теоретического распред-я наз-ся отн-е центр. момента 3-го пор-ка к кубу ср. квадр. ожидания. A= μ₃/ 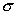в кубе. А=0, если распред-е симметрично относ-но мат. ожидания. Для оценки крутости теоретич. расп-я примен-ся эксцесс, кот. опр-ся так 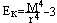30. Неравенство Маркова.Если СВ Х принимает неотрицательные значения, т.е. (х≥0, х_i≥0) и существует ее мат. ожидание M(x)=a, то для А числа ε>0 выполняется неравенства:P(x≥ε)< или P(x<ε)≥1- . Событие x<ε, x≥ε след. сумма вероятностей этих событий =1. P(x<ε)+P(x≥ε)=1

31. Неравенство Чебышева.Если Х-СВ, мат. ожидание к-рой М(Х) = а, а дисперсия D(Х) конечна, то д/любого числа ε > 0 выполняются неравенства:

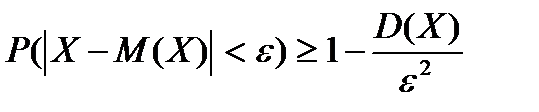
При неизв-ом з-не распред-я на практике при известных М(Х),D(X) участком возможных значений СВ Х считают М(Х)±3σ(Х)

32. Теорема Чебышева.Если СВ-ы Х1, Х2….Хn независимы и имеют мат. ожид. M(x1), M(x2)….M(xn) и дисперсии D(x1), D(x2)…..D(xn), кот. Ограничены одним и тем же числом С, то для А δ>0, вып. неравенство:

P(|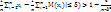

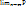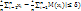Следствие:1. (| =12. Если все СВ Хi имеют одно и тоже мат. ожидание M(xi)=a, i=1,n, то неравенство примет вид:P(| 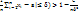Отсюда следует, что среднее арифметическое при большом n как угодно мало отличается от постоянной величины a.

33. Теорема Бернулли. Значение закона больших чисел.Если вероятность наступления события А в каж-м из n повторных независимых испытаний постоянна, то при неограниченном увеличении числа n исп-й отн-я частота 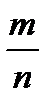наст-я соб-я А стрем-ся по вер-ти к числу p, т.е. для 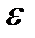>0 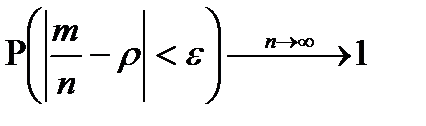Т-ма Б-ли явл-ся теор-ким обосн-ем для стат-го опр-я вер-ти.

Неравенство Бернулли:Пусть 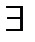n исп-й Бернулли с вер-ю успеха p, q=1-p и m – число успехов. Тогда для 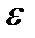>0

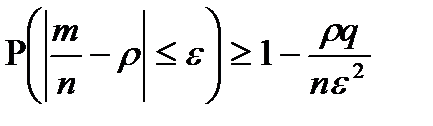
34. Понятие о центральной предельной теореме. Суть центральной предельной теоремы (ЦПТ) в след.: Если СВ х представляет собой сумму оч. большого числа взаимно независимых случ. в-н, влияние каждой из которых на всю сумму ничтожно мало, то х имеет расп-е, близкое к нормальному. Центральная предельная теорема (ЦПТ) ( в формулировке Ляпунова А.М. для одинаково распред. СВ). Если попарно независимые СВ X1, X2, ..., Xn, ... имеют одинаковый закон распределения с конечными числовыми характеристиками M[Xi] = m и D[Xi] = s2, то при n ® ¥ закон распределения СВ 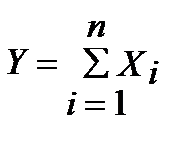неограниченно приближается к норм. закону N(n×m, 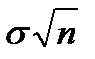). Следствие. Если в условии теоремы СВ 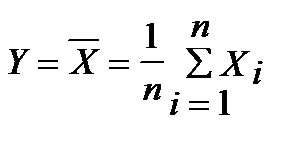, то при n ® ¥ закон распределения СВ Y неограниченно приближается к нормальному закону N(m, s/ ).

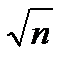35. Предмет и метод мат. статистики.МС – раздел мат-ки, изуч. методы сбора, систематизации и обработки рез-тов набл-й с целью выявления стат. зак-стей. Оперирует непосредственно с р-тами наблюдений над случ. явлением. Предметом МС явл. изуч-е случ. событий и случ. величин по р-там наблюд-й. Задачи МС: 1.указать способы сбора и группировки стат. сведений, получ. в р-те наблюдений или в р-те спец. поставл. экспер-тов; 2.разработать методы анализа стат. данных в зав-сти от целей иссл-я. Осн. задача МС сост. в получ-и выводов о массов. явлениях по данных наблюдения за ними. МС опирается на ТВ. Ее цель-оценить характер-ки генер. совок-ти по выборочным данным. Стат. совок-сть – совок-сть предметов или явл-й объед. каким-л. общим признаком. Р-том наблюд-й над ста. совок-стью явл. стат. данные. Обработка стат. данных методами МС приводит к установл-ю опред. законом-стей, присущих массовым явл-ям.

36. Генеральная и выборочная совокупности. Способы отбора.Вся подлежащая изучению совокупность предметов называется генеральной совокупностью. В статистике различают два вида наблюдений: сплошное, когда изучаются все объекты совокупности и несплошное (выборочное), когда изучается только часть объектов.Та часть объектов, которая отобрана для непосредственного изучения из генер. совокупности, называется выборочной совокупностью или выборкой. Кол-во объектов генер. или выбор. совокуп-ти называют объемом. Сплошное набл. применяют когда объем генер. совок. небольшой. Результаты исследования некот. признака генер. совок-ти будут более достоверными, если выборка образовано случайно (элементы берутся наугад и каждый из них может быть отобран с одинаковой вероятностью. Бесповторная выборка – из генер. совок-ти элементы извлекаются и не возвращаются обратно. Если после извлечения элементов из совок-ти они фиксируются и возвращаются обратно – повторный отбор.

37. Постр-е дискретного вар. ряда. Эмпир. функция распр-я и ее св-ва.Пусть из генер. совок. извлечена выборка v, причем значения 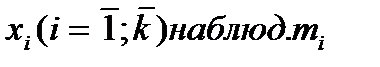раз.. Тогда наблюдаемые случ. значения xi наз. вариантами, mi – частотами. 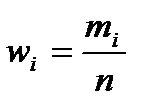- относ. частотами. А последов-ть вариант (xi),запис. в возрастающем порядке, наз. вариац. рядом. Стат. распред-ем наз. перечень вариант и соотв. им частот, или относит. частот. Стат. распред. можно изобр. графически. Для этого на Ох наносят xi, а на Оу – частоты mi. Соединив точки частот, получим ломаную, кот. наз-ся полигоном распред-я. В завис-ти от того, какие знач. принимает признак стат. распред., вариац. ряды дел. на Дискретные (варианты приним. конкр. значения) и Интервальные (варианты изменяются непрерывно в некот.интервале). Эмпир.функция распр-я.Пусть известно стат. распр-е колич. признака А; nx – число наблюдений, при кот-х наблюдалось знач-е признака, меньшее x , т.е. А< x; n – общее число наблюдений (объём выборки). Тогда относ. частота события А< x есть nx/n. При изм-и x меняется и nx/n, т.е. относительная част. nx/n является функцией x . Так как эта функция находится эмпир. (т.е. опытным) путём, то её наз. эмпирической. Эмпир. функцией распр-я (функцией распр-я выборки) наз. функция 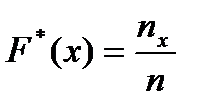опред. для каждого знач-я xÎR относ. частоту события А< x. В этой ф-ле nx – число вариант, меньших x, поэтому для расчетов удобна ф-ла вида .

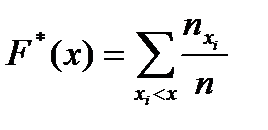38. Построение интерв. вариац. ряда. Гистограмма частот и относ. частот.При большом объеме выборки ее элементы объед. в группы (разряды, интервалы), представляя р-ты опытов в виде интерв. стат. ряда. Для этого весь диапазон значений СВ x (от xmin до xmax ) разбивают на k интервалов одинак. длины h (обычно k меняется от 5 до 20). Число интервалов рекомендуют брать согласно формуле Стерджеса k =1+ 3,93× ln n Затем подсчит. частоты ni (или относит. частоты wi ) знач-й выборки, попавших в выдел. интервалы. Величина ni/h наз. плотностью частоты, а wi/h – плотностью относ. частоты. Пусть xi*– середина i -го интервала, ni – число эл-тов выборки, попавших в i -й интервал. Таким образом, получим группиров. стат. ряд, в верхней строке которого записаны середины соотв. интервалов xi*: xi* x1* x2* …xk*; ni n1 n2 … nk.

Для граф. представления интерв. стат. распределений принято использовать гистограмму относ. частот. Гистограммой относ. частот интервального стат. ряда наз. ступенчатая фигура, составл. из прямоугольников, постр. на интервалах группировки длины h и высоты wi/h так, что площадь каждого прямоугольника равна относительной частоте wi. Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки длиной wi/h параллельно оси ординат. Очевидно, площадь i -го частичного прямоугольника равна wi – относительной частоте вариант, попавших в i -ый интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот (т.е. равна 1), а площадь гистограммы частот равна объему выборки n .

ух ух=ах+в   ах+в ухi     х

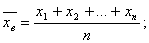39. Выборочная средняя, выборочная дисперсия и их свойстваВыборочная средняя. Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n. Выборочной средней называют среднее арифметическое значение признака выборочной совокупности. Если все значения признака выборки различны, то если же все значения имеют частоты n1, n2,…,nk, то 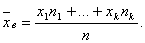Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней. Замечание: Если выборка представлена интервальным вариационным рядом, то за xi принимают середины частичных интервалов. Выборочная дисперсия. Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения, вводят сводную характеристику- выборочную дисперсию. Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения . Если все значения признака выборки различны, то 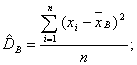если же все значения имеют частоты n1, n2,…,nk, то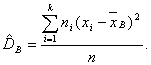

41. Интервальные оценки числовых характеристик случайной величины. Доверительная вероятность. Доверительный интервал.Пусть сделана выборка объема n. Для оценки распределения СВ Х генеральной совокупности применяются точечные оценки параметров распределения генеральной совокупности и интервальные оценки. Интервальной оценкой (доверительным интервалом) для оценки некоторого параметра q (тэта), например МО, называется угловой интервал 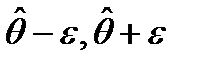, в котором с заранее заданной вероятностью Р=1-a содержится оцениваемый параметр. Опр.: Доверительным интервалом для оценки параметра q назыв. интервал 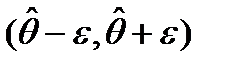для которого 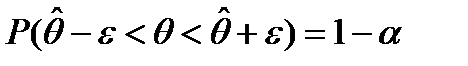. Вероятность Р=1-a - называется доверительной вероятностью.

Выбор доверительной вероятности Р=1-a производится исходя из конкретных условий задачи.

42. Основные понятия регрессионного и корреляционного анализа.Функцион. зависимость м-ду величинами X и Y - каждому значению одной переменной соответствует вполне опред. значение другой. Статистической наз.т зависимость, при которой изменение одной из величин влечет изменение распределения другой. Статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой. Корреляционной (или регрессионной) зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой. Условное мат. ожидание Mx (Y) СВ Y есть функция от x : Mx (Y) = f (x) , которую называют функцией регрессии Y на X . Корреляц. зависимостью Y от X называется функц. зависимость условной средней 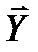x от x . Уравнение y = f (x) наз. уравн-ем регрессии Y на X . Функция f (x) наз. регрессией Y на X , а ее график – линией регрессии СВ Y на СВ X . Осн. задачи теории корреляции: 1. Установл. формы корреляционной связи; 2. Оценка тесноты корреляционной связи Y от X , кот. оценивается величиной рассеяния значений Y около Yx. Большое рассеяние означает слабую зависимость Y от X либо вообще отсутствие таковой. Малое рассеяние указывает на существование достаточно сильной зависимости Y от X . Важной с точки зрения приложений является ситуация, когда обе функции регрессии f (x),j ( y) являются линейными. Тогда говорят, что СВ X и Y связаны линейной корреляц. зав-стью (линейной корреляцией).

40. Точечное оцен-е числ. хар-к СВ. Состоят-сть, эффективность, несмещенность оценки. Исправл. выбор. дисперсия. Точ. оценкой хар-ки θ наз. некот. ф-цию 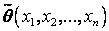р-тов наблюд-й, знач-я кот-ой близки к неизв. хар-ке θ генер. совок-сти. Для постр-я оценки нужны критерии.1. Оценка 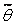наз. несмещ., если её мат. ожид-е равно оцениваемой хар-ке СВ: 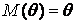, (1.1) т. е. если она не дает системат. ошибки. 2. Оценка наз. состоят., если при увел-и числа набл-й оценка сходится по вероятности к искомой вел-не, т. е. для любого сколь угодно малого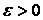 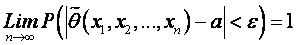. (1.2) Состоят-сть означ., что оценка, постр. по большому числу наблюд-й, имеет меньший разброс (дисперсию), т. е. 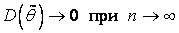. Желательно иметь оценки, кот-е имеют наим. дисперсию среди всех оценок, постр. по n набл-ям. Такие оценки наз. эффективн.. Точечная оценка мат. ожидания. Задана СВ Х: х1, х2, …, хn, так как М(Х) не найти, то для мат. ожид-я СВ Х естественно предложить ср. ариф-кое 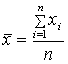(1.3) её наблюд. значений.1. По методу произведений 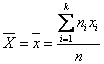, ,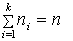т. к. 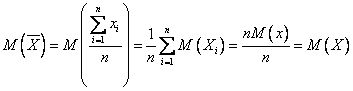. Это и означ., что оценка 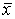несмещ.. 2. Если исслед. СВ Х имеет конечную дисперсию, то эта оценка будет состоят., т. к. 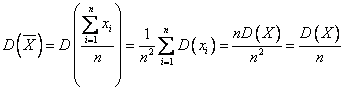. Если иссл. в-на имеет норм. закон распр-я, то можно показать, что предл. оценка эффективна, т. е. оценки для мат. ожид-я с меньшей дисперсией не сущ. для нормально распр. вел-н. Точечная оценка для дисперсии. Т к. дисп-я опр-ся через мат. ожид-е, а для него оценка уже выбрана, то для Д естественно предложить оценку: 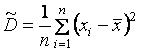или 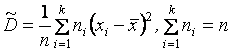; (1.4) ,(1.5) что соотв. записи Д в виде 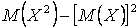.Оказ-ся, что предл. оценка Д (1.4) состоятельна и (1.5) не явл. несмещ.. Для получ-я несмещ. оценки введем поправку и получ. оценку обозн. через S2: 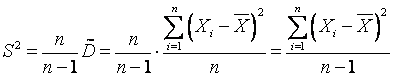или 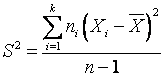.- исправл. выбор. Д.

43.Нахождение параметров линейного уравнения регрессии методом наименьших квадратов.Составив таблицу зависимости у_х(_{сверху черточка}) от х построим точки с координатами (х_i,y_xi). По расположение точек и исходя из существа величин х,у выбираем вид уравнения регрессии: прямая линия или параболическая зависимость или показательная и т.д. Пусть выбрана для представления уравнения регрессии прямая линия, т.е. корреляционная зависимость линейная.

Ищем уравнение прямой линии регрессии в виде у_х=ах+в. Чтобы прямая проходила как можно ближе к точкам выбираем следующее условие: Сумма квадратов разностей между экспериментальными ординатами y_i и теоретическими а_xi+в должна быть наименьшей. В этом суть метода наименьших квадратов. 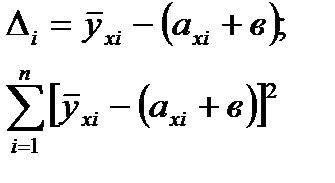При этом помним, что х_i y_xi (_{c черточкой над у}) известные нам числа. Неизвестными явл. а и в.

44. Коэффициент линейной корреляции и его свойства. - корреляционный момент (ковариация), где K(X ,Y ) = = M{[X -M(X )][Y -M(Y)]} Две случайные величины X и Y называются коррелированными, если их коэф-т корреляции отличен от нуля. СВ X и Y называются некоррелированными, если их корреляционный момент равен нулю. выборочный коэф. коррел. Свойства коэф-та корреляции: 1. Коэф-т корреляции принимает значения на отрезке [-1;1], т.е. 1 1 в -1 £ r £ 1; 2.Если все значения переменных увеличить (уменьшить) на одно и то же число или в одно и то же число раз, то величина выборочного коэф-та корреляции не изменится. 3.При 1 r = ±1 корреляц. связь представл. линейную функц. зависимость. При этом линии регрессии Y на X и X на Y совпадают, все наблюдаемые значения располагаются на общей прямой. 4.Если с ростом значений одной СВ значения второй возрастают, то 0 в r > , если убывают, то 0 в r < . 5.При 0 в r = линейная корреляц. связь отсутствует, групповые средние переменных совпадают с их общими средними, а линии регрессии Y на X и X на Y параллельны осям координат. Выборочный коэф-т корреляции r является оценкой генерального коэф-та корреляции

45. Стат. гипотеза. Стат. критерий проверки гипотез. Ошибки 1 и 2 рода. Критич. область.Стат. гипотеза – любое предпол. относит. генер. сов-ти, кот. проверяется путем анализа данных выборки. Выдвинутую гипотезу наз. основной или нулевой Но. наряду с Но рассм. противоречащую ей гипотезу Н1, кот. наз-ся альтернативной или конкурирующей. Выдвинутая гипотеза должна быть проверена стат. методами. По итогам проверки гипотеза либо принимается, либо отклоняется. При этом могут быть допущены ошибки 2 родов: ошибки 1 рода сост. в том, что будет принята гипотеза Н1, в то время как верной явл. гипотеза Но. Вер-ть ошибки 1 рода обозн. 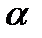и ее наз. уровнем 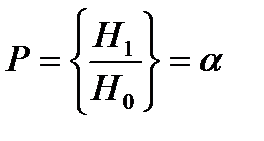. Ошибка 2 рода сост. в том, что будет принята гипотеза Но, в то время как верной явл. гипотеза Н1. Вероятность ош. 2 рода обозн.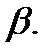 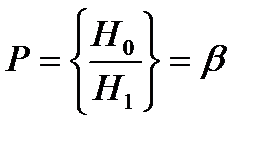. Стат. критерием наз. СВ К, кот. служит для проверки нулевой гипотезы. Множ-во всех возм. значений критерия К разбивается на 2 непересек. подмнож-ва – критич. область (мн-во значений критерия, при кот. нулевую гипотезу отвергают) и обл. принятия гипотезы (мн-во значений критерия, при кот. нулевую принимают). По данным выб-ки выч-ся значение К наблюдаемое, кот. наз. наблюдаемым знач-ем. Правило проверки стат. гипот.:если значение К набл. попадает в обл. принятия, то Но приним-ся; если значен. К набл. попадает в критич. обл., то гип. Но отверг-ся. Мощностью критерия наз. вер-ть того, что будет принята конкурир. гипотеза Н1 если она явл. верной. Если 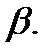- вер-ть ошибки 2 рода, то мощн-ть критерия = 1-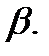

46. Проверка гипотезы о математическом ожидании нормально распределенной случайной величины.Пусть имеется нормально распр. СВ x,, опред. на мн-стве объектов некот. генер.сов-сти. Известно, что Dx = s ². Мат. ожидание Mx неизвестно. Допустим, что Mx = a, где a – некот. число. Будем считать также, что имеется другая информация, что Mx = a₁, где a₁ > a. I. Выдвиг. нулевую гипотезу H₀: Mx = a при конкур. гипотезе H₁: Mx = a₁. Делаем выборку объема n: x₁, x₂,..., x_n . В основе проверки лежит тот факт, что случ. вел-на 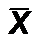(выбор. средняя) распр-на по норм. закону с дисперсией s ²/n и мат.ож-ем, равным a в случае справ-сти H₀, и равным a₁ в случае справ-сти H₁.Очевидно, что если вел-на 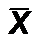оказ. достаточно малой, то это дает основ-е предпочесть г-зу H₀ г-зе H₁. При дост-но большом знач-и 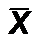более вероятна справ-сть гипотезы H₁. В кач. стат. критерия выбир. СВ. Z = (x с чертой – а)*(корень из n)/(ср. кв. откл-е), распр. по норм. закону, причем Mz = 0 и Dz = 1 в случае справ-сти гипотезы H₀. Если справедл. гипотеза H₁, то
Mz = a* = ( a₁ – a ) 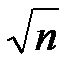/s, Dz = 1.Если вел-на 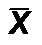, получ. из вы­бор. данных, относ-но велика, то и вел-на z велика, что явл. свид-вом в пользу г-зы H₁. Относ-но малые знач-я 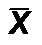приводят к малым знач-ям z, что свид-вует в пользу г-зы H₀. Отсюда следует, что д. б. выбрана правостор. крит. область. По принятому уровню знач-сти a (напр., a = 0,05), используя то, что СВ z распр-на по норм. закону, опр. знач-е K_кр из ф-лы a = P(K_кр < z <¥) = F(¥) – F(K_кр) = 0,5 – F(K_кр).Отсюда Ф(К_кр)=(1-2альфа)/2. Если в-на z, получ. при выбор. знач-и 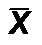, попад. в область принятия г-зы (z < K_кр), то г-за H₀ приним. Если в-на z попад. в крит. область, то г-за H₀ отверг. II. Если в предыд. задаче поставить др. условие: H₀: Mx = a; H₁: Mx = a₁ , a₁ < a, то здесь придется рассм. левостор. крит. область. Здесь a* = ( a₁ – a ) 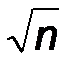/s, а вел-на K_кр опр. из ф-лы a = P(–¥ <z< K_кр) = F( K_кр) –F(–¥) = F( K_кр) + 1/2.Используя формулу –F( K_кр) = F( –K_кр), получаем: F( –K_кр)=(1-2альфа)/2. Знач-я z, вычисл. по выбор. данным, превыш. K_кр, согласуются с г-зой H₀. Если в-на z попад. в крит. область (z < K_кр), то г-зу H₀ следует отвергнуть, считая предпочт. г-зу H₁.III. Рассмотрим теперь такую задачу: H₀: Mx = a; H₁: Mx ¹ a. В данном случае следует рассм. двустор. крит. область. Крит. знач-е K_кр опр-ся с пом. соотн-я P(–K_кр < z < K_кр) = 1 – a = F( K_кр) –F( – K_кр) = 2F( K_кр) .Из этого соотн-я следует: F( K_кр) = )=(1-альфа)/2.

47. Проверка гипотезы о равенстве математических ожиданий двух нормально распределенных случайных величин.Предполож., что имеются случ. выборки х₁, х₂, ..., х_п и y₁, y₂, ..., y_m знач-й двух независ. нормально распред. СВ 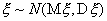и 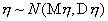и требуется проверить гипотезу 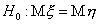о рав-ве мат. ожиданий этих СВ. (а) Если известно, что дисперсии случайных величин x и h равны, 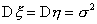(значение 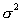неизвестно), то можно получить след. объедин.несмещ. оценку для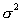 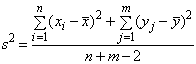В этом сл. s²/n и s²/m будут несмещ. оценками для дисперсии выборочных средних 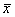и 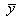, а сумма s²/n+s²/m – несмещ. оценкой для дисперсии разности средних 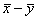. Соотв-но, статистика 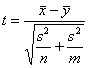как можно показать, будет иметь t-распред-е с n+m-2 степенями свободы. Крит. область уровня 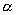для проверки гипотезы 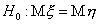против двустор. альтернативы 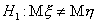будет состоять из двух бесконечных полуинтервалов 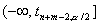и 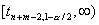, против одностор. альтернативы 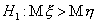- из полуинтервала 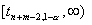и против альтернативы 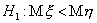- из полуинт-ла 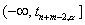, где 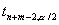, , 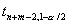, 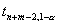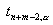обознач. соотв. квантили t-распред-я с n+m-2 степенями свободы.

(б) Если нет оснований считать, что дисперсии СВ x и h равны, то для каждой из дисперси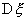й и 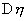вычисл. своя оценка и соотв-нно модифиц. статистика критерия 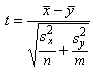которая, как можно показать, имеет t-распред-е с числом степеней свободы, равным целой части от 1/k, где k выражается след. формулой

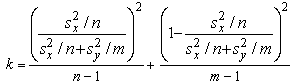
48. Критерий согласия Пирсона о предполагаемом законе распределения случайной величины.1.) Исходя из теоретического (предполагаемого закона распределения), находим вероятности р­_i попадания СВ в каждый из заданных интервалов таблицы, например в случае нормального распределения .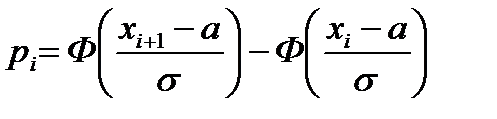

2.) Вычисляем значение c² соответствующее опытным данным по формуле: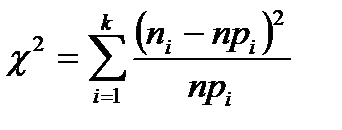

3.) По табл. критических точек c², учитывая число степеней свободы k=m-r-1, где m – число интервалов, r – число оцениваемых параметров в распределении (для нормального распределения r=2) – находим по таблице c²_крит.

4.) Если c²_{вычисленное}<c²_крит., то гипотеза о нормальном распределении принимается. Если же c²_{вычисленное}>c²_крит., гипотеза отвергается.

Замечание: При нахождении c²_крит. учитывается уровень значимости критерия, который обозначается a(q). Уровень значимости критерия для технических задач обычно принимается a=0,05. Он означает вероятность того, что событие не наступит при данных условиях.

49. Критерий согласия Колмогорова о предполагаемом законе распределения случайной величины.1.) По результатам n – независимых опытов найти эмпирическую функцию распределения: F^*(x)

2.) Определить максимум модуля: |F^*(x)-F(x)| во всех точках.

3.) Вычислить выборочную статистику .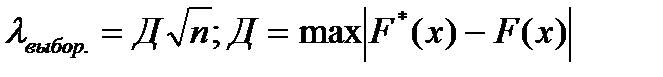

4.) Сравниваем значения l_{выборочн.} с критическим значением l, определенным по табл. 5.) Если l_{выборочн}<l_крит. – гипотеза принимается, если l_{выборочн}>l_крит. – гипотеза отвергается.

50. Основные понятия дисперсионного анализа. Однофакторный и двухфакторный дисперсионный анализДисперсионный анализ примен.для исслед-я влияния 1 или неск.кач. переменных на 1 завис.колич.пер-ную . В основе дисперс. анализа лежит предпол-е о том, что одни переменные могут рассматриваться как причины (независ. переменные): , а другие как следствия (завис.переменные). Независ. переменные наз. иногда регулир. ф-рами именно потому, что в эксперименте иссл-ль имеет возм-сть варьировать ими и анализ-ть получающийся рез-т.Осн. целью дисперс. анализа явл. исслед-е значимости различия между средними с пом. сравнения (анализа) дисперсий. Раздел-е общей дисперсии на несколько источников, позволяет сравнить дисперсию, вызванную различием между группами, с дисперсией, вызванной внутригрупп. изменчивостью. При истинности нулевой гипотезы (о равенстве средних в неск. группах наблюдений, выбранных из генер. совок-сти), оценка дисперсии, связанной с внутригруп. изменчивостью, д. б. близкой к оценке межгрупп. дисперсии. Сущность дисп. анализа закл. в расчленении общей дисперсии изуч. признака на отд. компоненты, обусловл. влиянием конкр. ф-ров, и проверке гипотез о значимости влияния этих ф-ров на исслед. признак. Сравнивая комп-ты дисперсии друг с другом посредством F—критерия Фишера, можно определить, какая доля общей вариативности результат. признака обусловлена действием регулир. ф-ров. Исходным мат-лом для дисп.анализа служат данные исслед-я 3 и более выборок: , которые могут быть как равными, так и неравными по численности, как связными, так и несвязными. По кол-ву выявляемых регулир. ф-ров дисп. анализ м. б. однофакт. (при этом изуч. влияние 1 фактора на рез-ты эксперимента), двухфакт. (при изучении влияния двух факторов) и многофакт. (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие). Дисп. анализ относится к группе параметрич. методов и поэтому его следует применять только тогда, когда доказано, что распред-е явл. нормальным. Дисп. анализ исп., если зависимая переменная измер. в шкале отношений, интервалов или порядка, а влияющие переменные имеют нечисловую природу (шкала наименований).