Примеры решения систем линейных алгебраических уравнений методом Крамера
Разберем решения нескольких примеров.
Пример.
Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера 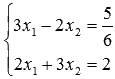 .
.
Решение.
Основная матрица системы имеет вид 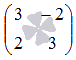 . Вычислим ее определитель по формуле
. Вычислим ее определитель по формуле 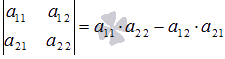 :
:
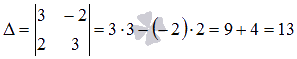
Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определители 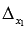 и
и 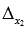 . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель
. Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель 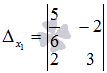 . Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем
. Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем 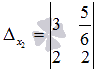 .
.
Вычисляем эти определители:
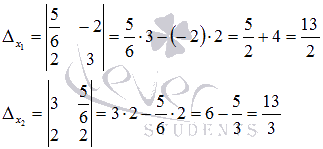
Находим неизвестные переменные x1 и x2 по формулам 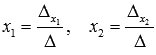 :
:
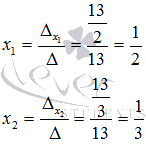
Выполним проверку. Подставим полученные значения x1 и x2 в исходную систему уравнений:
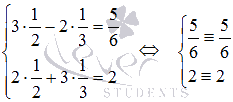
Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
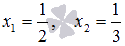 .
.
Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.
Пример.
Найдите решение системы линейных уравнений методом Крамера 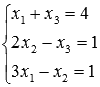 .
.
Решение.
Перепишем систему в виде 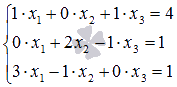 , чтобы стало видно основную матрицу системы
, чтобы стало видно основную матрицу системы 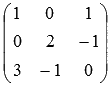 . Найдем ее определитель по формуле
. Найдем ее определитель по формуле
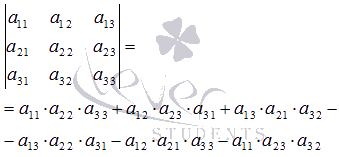
Имеем
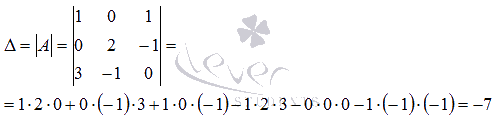
Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители 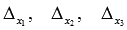 :
:

Таким образом,
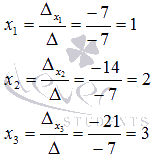
Ответ:
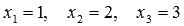 .
.
Обозначения неизвестных переменных в уравнениях системы могут отличаться от x1, x2, …, xn. Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.
Пример.
Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными 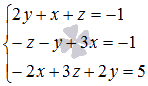 .
.
Решение.
В данном примере неизвестные переменные имеют другое обозначение (x, y и z вместоx1, x2 и x3). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать 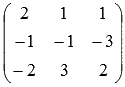 . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как
. Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как 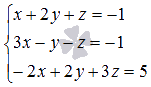 . Теперь основную матрицу системы хорошо видно
. Теперь основную матрицу системы хорошо видно 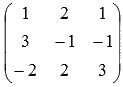 . Вычислим ее определитель:
. Вычислим ее определитель:
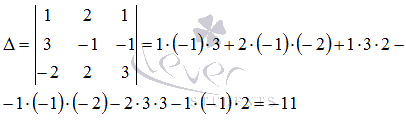
Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители 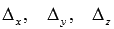 (обратите внимание на обозначения) и вычислим их:
(обратите внимание на обозначения) и вычислим их:
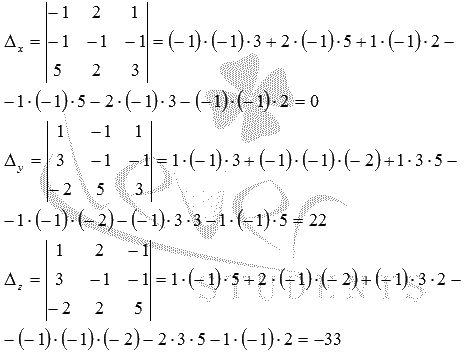
Осталось найти неизвестные переменные по формулам 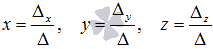 :
:
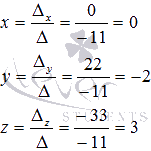
Выполним проверку. Для этого умножим основную матрицу на полученное решение  (при необходимости смотрите раздел операции над матрицами):
(при необходимости смотрите раздел операции над матрицами):
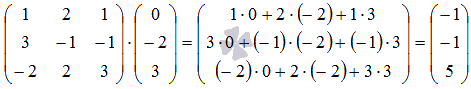
В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.
Ответ:
x = 0, y = -2, z = 3.
Пример.
Решите методом Крамера систему линейных уравнений 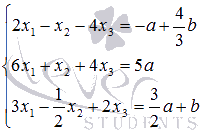 , гдеa и b – некоторые действительные числа.
, гдеa и b – некоторые действительные числа.
Решение.
Вычислим определитель основной матрицы системы:
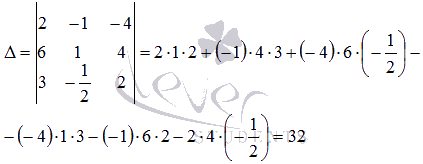
Определитель отличен от нуля, следовательно, можно применить метод Крамера.
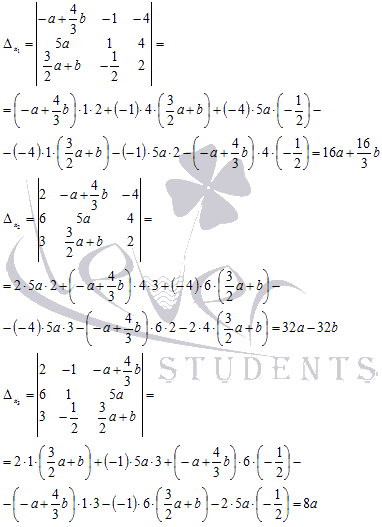
Находим неизвестные переменные
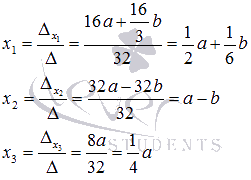
Рекомендуем проверить полученные результаты.
Ответ:
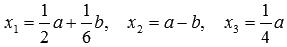 .
.
Пример.
Найдите решение системы уравнений 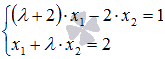 методом Крамера,
методом Крамера, 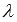 - некоторое действительное число.
- некоторое действительное число.
Решение.
Вычислим определитель основной матрицы системы: 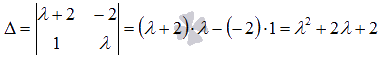 . Область значений выражения
. Область значений выражения 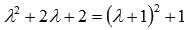 есть интервал
есть интервал 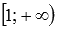 , поэтому
, поэтому 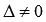 при любых действительных значениях
при любых действительных значениях 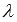 . Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляем
. Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляем 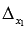 и
и 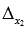 :
:
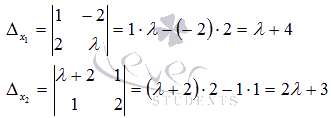
Таким образом, 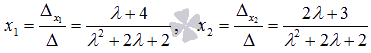 .
.
Выполним проверку:
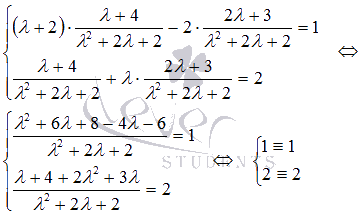
Уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
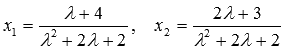 .
.
Пример.
Решите систему линейных алгебраических уравнений методом Крамера 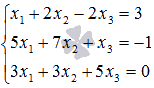 .
.
Решение.
Вычислим определитель основной матрицы системы уравнений:
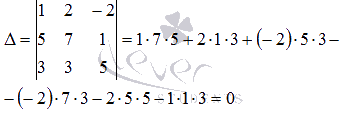
Определитель основной матрицы равен нулю, следовательно, метод Крамера не подходит для решения такой системы уравнений.
Пример.
Методом Крамера найдите решение СЛАУ 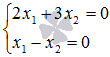 .
.
Решение.
Эта система однородная, так как все свободные члены равны нулю. Определитель основной матрицы отличен от нуля 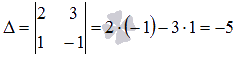 , поэтому ее единственным решением является x1 = 0, x2 = 0. О таких СЛАУ мы уже упоминали вышев замечании.
, поэтому ее единственным решением является x1 = 0, x2 = 0. О таких СЛАУ мы уже упоминали вышев замечании.
Ответ:
x1 = 0, x2 = 0.
Пример.
Найдите решение системы четырех линейных алгебраических уравнений 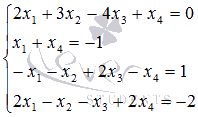 содержащую четыре неизвестных переменных.
содержащую четыре неизвестных переменных.
Решение.
Сразу скажем, что не будем подробно описывать вычисление определителей матриц, так как это выходит за рамки данной статьи.
Вычислим определитель основной матрицы системы, разложив его по элементам второй строки:
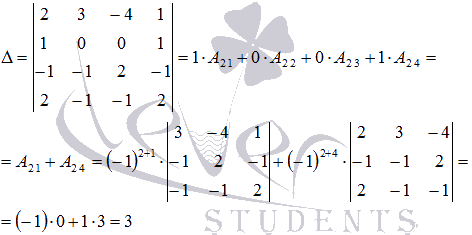
Определитель основной матрицы системы отличен от нуля, поэтому можно воспользоваться методом Крамера для решения системы.
Найдем 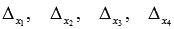 :
:
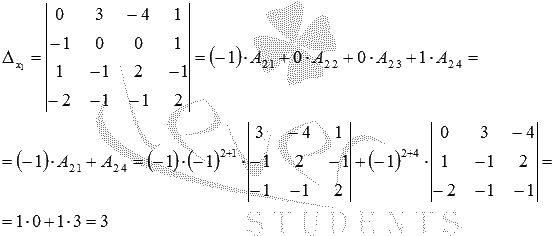
аналогично вычисляются
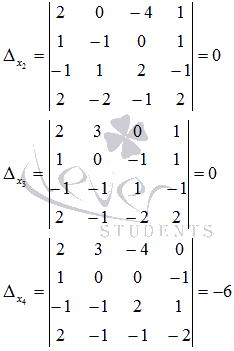
Таким образом,
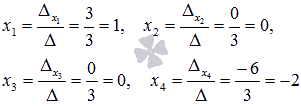
Ответ:
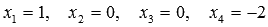 .
.
К началу страницы
Подведем итог.
Метод Крамера позволяет находить решение систем линейных алгебраических уравнений, если определитель основной матрицы отличен от нуля. По сути метод сводится к вычислению определителей матриц порядка n на n и применению соответствующих формул для нахождения неизвестных переменных.
