Кривые второго порядка. Канонические уравнения окружности, эллипса, гиперболы и параболы. Их основные свойства

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

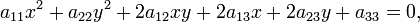
в котором по крайней мере один из коэффициентов 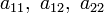отличен от нуля.

Центр окружности – это геометрическое место точек в плоскости равностоящих от точки плоскости С(а,b).

Окружность задается следующим уравнением:

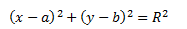
Где х,у – координаты произвольной точки окружности, R - радиус окружности.

Признак уравнения окружности

1. Отсутствует слагаемое с х,у

2. Равны Коэффициенты при х² и у²

Эллипсом называется геометрическое место точек в плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости называется фокусами (постоянная величина).

Каноническое уравнение эллипса:

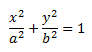
Х и у принадлежат эллипсу.

а – большая полуось эллипса

b – малая полуось эллипса

У эллипса 2 оси симметрии ОХ и ОУ. Оси симметрии эллипса – его оси, точка их пересечения – центр эллипса. Та ось на которой расположены фокусы, называется фокальной осью. Точка пересечения эллипса с осями – вершина эллипса.

Коэффициент сжатия (растяжения): ε = с/а – эксцентриситет (характеризует форму эллипса), чем он меньше, тем меньше вытянут эллипс вдоль фокальной оси.

Если центры эллипса находятся не в центре С(α, β)

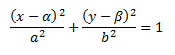
Свойства эллипса:

1) Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром - начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b (2a>2b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось - малой осью.

2) Весь эллипс содержится внутри прямоугольника

3) Эксцентриситет эллипса e < 1.

Действительно,

4) Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно а/е, а е<1, следовательно, а/е>a, а весь эллипс лежит в прямоугольнике)

5) Отношение расстояния ri от точки эллипса до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Доказательство.

Расстояния от точки М(х, у) до фокусов эллипса можно представить так:

Составим уравнения директрис:

(D1), (D2). Тогда Отсюда ri / di = e, что и требовалось доказать.

Гиперболой называется геометрическое место точек в плоскости, абсолютная величина разности расстояний, каждое из которых от двух данных точек этой плоскости, называемых фокусами есть величина постоянная , отличная от ноля.

Каноническое уравнение гиперболы

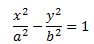
Гипербола имеет 2 оси симметрии:

а – действительная полуось симметрии

b – мнимая полуось симметрии

Свойства гиперболы:

1) Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах - ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2) Ветви гиперболы имеют две асимптоты, определяемые уравнениями

3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением, (11.3`) для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы e > 1.

5) Отношение расстояния ri от точки гиперболы до фокуса Fi к расстоянию di от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Доказательство можно провести так же, как и для эллипса.

Параболой называется геометрическое место точек в плоскости, равноудаленных от данной точки F, называемой фокусом и данной прямой, называемой директрисой.

Каноническое уравнение параболы:

У²=2рх, где р – расстояние от фокуса до директрисы (параметр параболы)

Если вершина параболы С (α, β), то уравнение параболы (у-β)²=2р(х-α)

Если фокальную ось принять за ось ординат, то уравнение параболы примет вид: х²=2qу

Свойства параболы:

1) Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной - начало координат.

2) Вся парабола расположена в правой полуплоскости плоскости Оху.

Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:

Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e<1), гиперболу (при e>1) или параболу (при е=1).