Горизонтальные асимптоты
Определение.
Если при 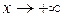 (
( 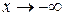 ) функция
) функция 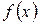 имеет конечный предел, равный числу b:
имеет конечный предел, равный числу b:
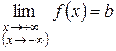 ,
,
то прямая 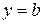 есть горизонтальная асимптота графика функции
есть горизонтальная асимптота графика функции 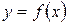 .
.
Например, для функции 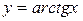 имеем
имеем
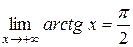 ,
, 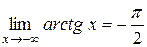 .
.
Соответственно, прямая 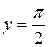 − горизонтальная асимптота для правой ветви графика функции
− горизонтальная асимптота для правой ветви графика функции 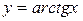 , а прямая
, а прямая 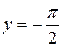 − для левой ветви.
− для левой ветви.
В том случае, если
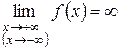 ,
,
график функции не имеет горизонтальных асимптот, но может иметь наклонные.
Наклонные асимптоты
Определение.
Прямая 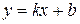 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 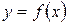 при
при 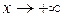 (
( 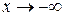 ), если выполняется равенство
), если выполняется равенство
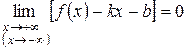 .
.
Наличие наклонной асимптоты устанавливают с помощью следующей теоремы.
Теорема.
Для того, чтобы график функции 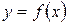 имел при
имел при 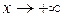 (
( 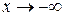 ) наклонную асимптоту
) наклонную асимптоту 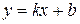 , необходимо и достаточно, чтобы существовали конечные пределы
, необходимо и достаточно, чтобы существовали конечные пределы
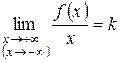 и
и 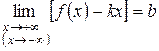 .
.
Если хотя бы один из этих пределов не существует или равен бесконечности, то кривая 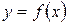 наклонной асимптоты не имеет.
наклонной асимптоты не имеет.
Замечания.
1. При отыскании асимптот следует отдельно рассматривать случаи 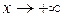 и
и 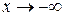 .
.
2. Если
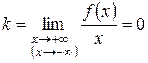 и
и 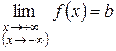 ,
,
то график функции 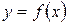 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту 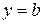 .
.
3. Если
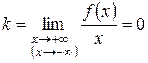 и
и 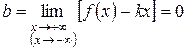 ,
,
то прямая 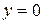 (ось Ох) является горизонтальной асимптотой графика функции
(ось Ох) является горизонтальной асимптотой графика функции 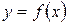 .
.
Из замечаний следует, что горизонтальную асимптоту можно рассматривать как частный случай наклонной асимптоты при 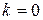 . Поэтому при отыскании асимптот графика функции рассматривают лишь два случая:
. Поэтому при отыскании асимптот графика функции рассматривают лишь два случая:
1) вертикальные асимптоты,
2) наклонные асимптоты.
Пример
Найти асимптоты графика функции 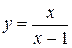 .
.
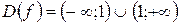 .
.
1) 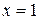 − точка разрыва второго рода:
− точка разрыва второго рода:
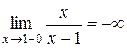 ,
, 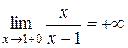 .
.
Прямая 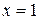 − вертикальная асимптота.
− вертикальная асимптота.
2) 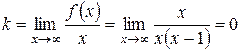 ,
,
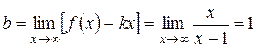 ,
,
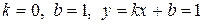 .
.
Прямая 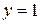 − горизонтальная асимптота. Наклонной асимптоты нет.
− горизонтальная асимптота. Наклонной асимптоты нет.
Общая схема исследования функции и построение графика
В предыдущих параграфах было показано, как с помощью производных двух первых порядков изучаются общие свойства функции. Пользуясь результатами этого изучения, можно составить представление о характере функции и, в частности, построить ее график.
Исследование функции 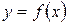 целесообразно проводить по следующей схеме.
целесообразно проводить по следующей схеме.
1. Найти область определения функции.
2. Исследовать функцию на четность и нечетность.
3. Исследовать функцию на периодичность.
4. Найти точки пересечения графика функции с осями координат.
5. Найти интервалы знакопостоянства функции (интервалы, на которых 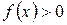 или
или 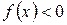 ).
).
6. Найти асимптоты графика функции.
7. Найти интервалы монотонности и точки экстремума функции.
8. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции.
9. Построить график функции.
Пример
Исследовать функцию 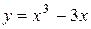 и построить ее график.
и построить ее график.
1. Область определения функции 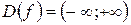 .
.
2. Функция нечетная: 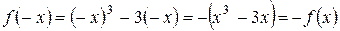 . График функции симметричен относительно начала координат
. График функции симметричен относительно начала координат
3. Функция непериодическая.
4. Точки пересечения с осями координат:
С осью Оу: 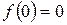 , точка
, точка 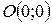 .
.
С осью Ох: 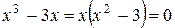 ,
, 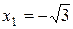 ,
, 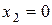 ,
, 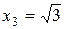 .
.
5. Точки 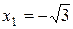 ,
, 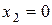 и
и 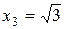 разбивают ось Ох на четыре интервала.
разбивают ось Ох на четыре интервала.
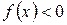 при
при 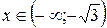 ;
;
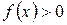 при
при 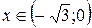 ;
;
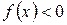 при
при 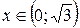 ;
;
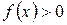 при
при 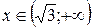 .
.
6. Так как функция является непрерывной, то ее график не имеет вертикальных асимптот.
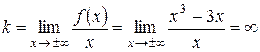 .
.
Наклонной и горизонтальной асимптот нет.
7. 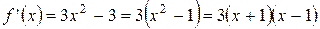 ,
,
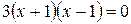 ,
, 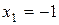 ,
, 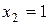 − критические точки.
− критические точки.
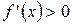 для
для 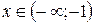 «↑»,
«↑»,
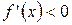 для
для 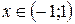 «↓»,
«↓»,
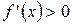 для
для 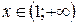 «↑».
«↑».
Сведем данные в таблицу.
| х | 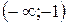 | -1 | 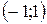 | 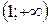 | |
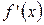 | + | − | + | ||
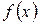 | ↑ (возрастает) | mах | ↓ (убывает) | min -2 | ↑ (возрастает) |
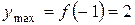 ,
, 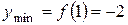 ;
;
точка 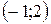 − максимум;
− максимум;
точка 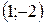 − минимум.
− минимум.
8. 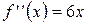 ,
, 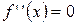 ,
, 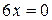 ,
, 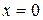 .
.
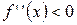 при
при 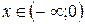 «
« 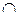 »;
»;
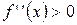 при
при 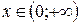 «
« 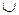 ».
».
| х | 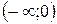 | 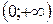 | |
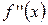 | − | + | |
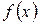 | 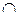 (выпуклый) (выпуклый) | (точка перегиба) |  (вогнутый) (вогнутый) |
Точка 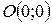 − точка перегиба.
− точка перегиба.
9. График функции 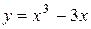 (рис.5.12)
(рис.5.12)
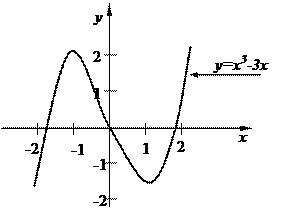 |
Рис. 5.12
Упражнения
Найти интервалы возрастания и убывания функций:
| 1. | 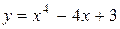 ; ; | Ответ: 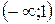 − убывает; − убывает; 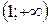 − возрастает. − возрастает. |
| 2. | 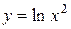 ; ; | Ответ: 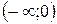 − убывает; − убывает; 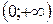 − возрастает. − возрастает. |
| 3. | 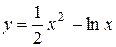 ; ; | Ответ: 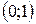 − убывает; − убывает; 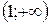 − возрастает. − возрастает. |
| 4. | 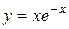 ; ; | Ответ: 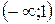 − возрастает; − возрастает; 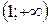 − убывает. − убывает. |
Найти экстремумы функций:
| 5. | 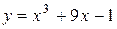 ; ; | Ответ: нет экстремума. |
| 6. | 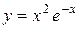 ; ; | Ответ: 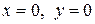 минимум, минимум, 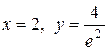 максимум. максимум. |
| 7. | 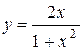 ; ; | Ответ: 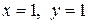 максимум, максимум, 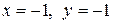 минимум. минимум. |
Найти наибольшее и наименьшее значения функции на указанных отрезках:
| 8. | 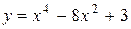 на на 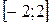 ; ; | Ответ: 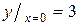 наибольшее, наибольшее, 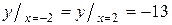 наименьшее. наименьшее. | |
| 9. | 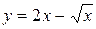 на на 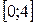 | Ответ: 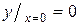 наименьшее, наименьшее, 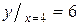 наибольшее. наибольшее. |
Найти интервалы выпуклости и вогнутости и точки перегиба графиков функций:
| 10. | 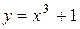 | Ответ: 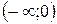 − выпуклость, − выпуклость, 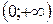 − вогнутость, − вогнутость, 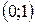 − точка перегиба. − точка перегиба. |
| 11. | 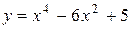 | Ответ: 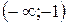 − вогнутость, − вогнутость, 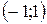 − выпуклость, − выпуклость, 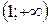 − вогнутость, − вогнутость, 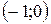 , , 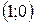 − точки перегиба. − точки перегиба. |
| 12. | 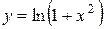 | Ответ: 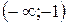 − выпуклость, − выпуклость, 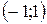 − вогнутость, − вогнутость, 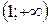 − выпуклость, − выпуклость, 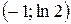 , , 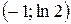 − точки перегиба. − точки перегиба. |
Найти асимптоты кривых:
| 13. | 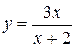 | Ответ: 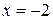 вертикальная; вертикальная; 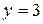 горизонтальная. горизонтальная. |
| 14. | 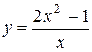 | Ответ: 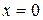 вертикальная; вертикальная; 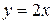 наклонная. наклонная. |
| 15. | 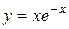 | Ответ: 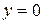 горизонтальная. горизонтальная. |
Исследовать функции и построить их графики:
| 16. | 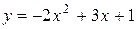 | |
| 17. | 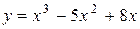 | |
| 18. | 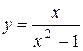 |
