Определение скорости и ускорения ведомого звена в исследуемом положении при помощи диаграмм

Определим значение скорости и ускорения точки D₁ по диаграмме.

Из диаграммы скоростей

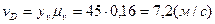
Из диаграммы ускорений

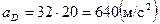
Построение плана скоростей для исследуемого положения и определение соответствующих кинематических параметров.

Рассмотрим построение плана скоростей для первого положения. Линейная скорость ведущей точки А:

,

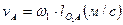где w₁-угловая скорость ведущего звена;

lO₁A - длина звена O₁A, м.

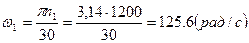
n₁- частота вращения звена O₁A, об/мин.

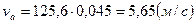
Скорость точки А изобразим в виде вектора Pa, длину которого примем 45 мм. Тогда масштабный коэффициент для построения плана скоростей:

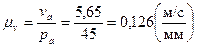
Скорость точки В определим из следующих векторных уравнений:

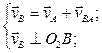
(Здесь 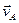известна и выражена на плане скоростей вектором 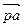; относительная скорость 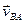представляет собой вектор, перпендикулярный звену АВ и проходящий через конец вектора 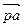; абсолютная скорость точки В изображается вектором, проходящим через полюс плана скоростей перпендикулярно О₂В. Пересечение проведенных двух направлений определяют положение точки В, изображающей конец вектора скорости 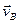и вектора ).

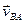Скорость точки С можно определить, если решить следующие векторные уравнения:

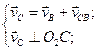
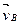Здесь известна и выражена на плане скоростей вектором 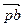; относительная скорость 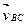представляет собой вектор, перпендикулярный звену CВ и проходящий через конец вектора 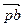; абсолютная скорость точки C изображается вектором, проходящим через полюс плана скоростей перпендикулярно О₂C. Пересечение проведенных двух направлений определяют положение точки C, изображающей конец вектора скорости 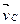и вектора .

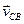Скорость точки D можно определить, если решить следующие векторные уравнения:

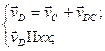
Здесь 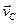известна и выражена на плане скоростей вектором 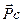; относительная скорость 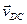представляет собой вектор, перпендикулярный звену CD и проходящий через конец вектора 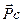; абсолютная скорость точки D изображается вектором, проходящим через полюс плана скоростей параллельно оси XX. Пересечение проведенных двух направлений определяют положение точки D, изображающей конец вектора скорости .

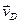Численную величину абсолютной и относительной скоростей любой точки механизма определяем умножением соответствующего вектора скорости, взятого из плана скоростей, на масштабный коэффициент.

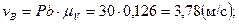
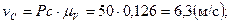
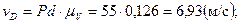
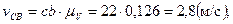
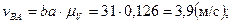
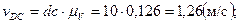
Определим угловые скорости звеньев:

;

.

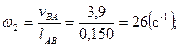
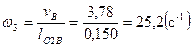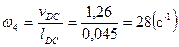Построение плана ускорений для исследуемого положения и определение соответствующих кинематических параметров

Рассмотрим построение плана ускорений для первого положения. Так как частота вращения ведущего звена постоянна, то точка А имеет только нормальное ускорение

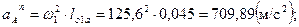
Из произвольной точки р строим вектор Pа=150мм, тогда масштабный коэффициент для плана ускорений:

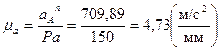
Вектор Pа направлен к центру вращения, то есть от точки А к точке О₁ параллельно О₁А.

Ускорение точки В определяется системой двух векторных уравнений:

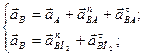
где 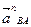- нормальное ускорение в относительном движении, направленное от точки В к А вдоль звена ВA;

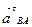- касательное ускорение в том же движении, направленное перпендикулярно звену ВA;

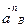- нормальное ускорение в абсолютном движении, направленное от точки В к O₂ вдоль звена ВO₂;

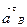- касательное ускорение в том же движении, направленное перпендикулярно звену ВO₂;

Вектор 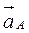известен из предыдущего, вектора

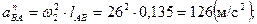
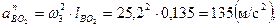
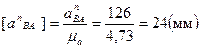
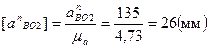
Ускорение точки C определим из уравнений:

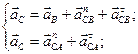
где 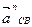- нормальное ускорение в относительном движении, направленное от точки C к B вдоль звена CB;

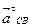- касательное ускорение в относительном движении, направленное перпендикулярно звену BC.

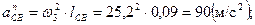
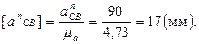
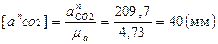
Ускорение точки D определим из уравнений:

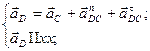
где 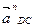- нормальное ускорение в относительном движении, направленное от точки D к C вдоль звена DC;

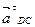- касательное ускорение в относительном движении, направленное перпендикулярно звену DC.

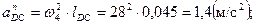
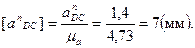
Определим величину ускорения точки D при помощи плана ускорений:

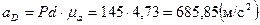
Найдем величину тангенциальной составляющей ускорения:

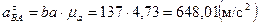
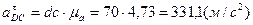
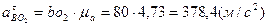
Определим угловые ускорения звеньев:

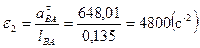
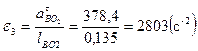
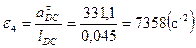
Из плана ускорений находим значение ускорения центра тяжести звена движущегося плоскопараллельно. В данном случае это однородное звено 2 и 4, центр тяжести которых находятся на их серединах (S2 и S4).

.
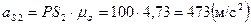