Наглядное изображение точки

Лекция 1

Тема: «Проецирование точки. Метод Монжа»

Условные обозначения и символы

Способы проецирования

Изображения объектов трехмерного пространства на плоскости получают методом проецирования. Аппарат проецирования включает в себя:

- проецирующие лучи, исходящие из центра проецирования S;

- проецируемый объект;

- плоскость, на которой получается изображение объекта.

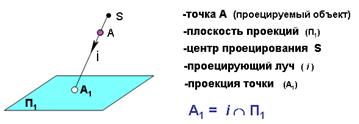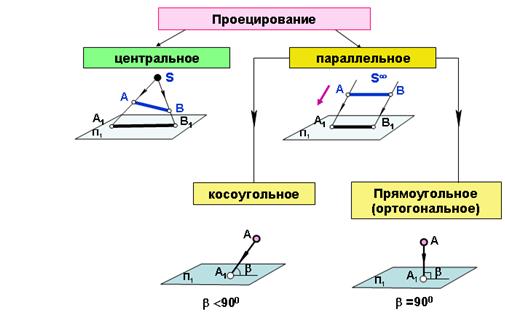
Проецирование может быть центральнымили параллельным.

При центральном проецировании проецирующие лучи выходят из одной точки – центра проецирования S, который находится на определенном (конечном) расстоянии от плоскости проекции.

При параллельном проецировании центр проецирования удален в бесконечность и все проецирующие лучи становятся параллельными. При этом, необходимо задать направление проецирования и плоскость проекций П₁.

В зависимости от направления проецирующих лучей по отношению к плоскости проекций параллельное проецирование может быть косоугольным,еслипроецирующие лучи не перпендикулярны к плоскости проекций или прямоугольным (ортогональным), если проецирующие лучи перпендикулярны к плоскости проекций.

Этот метод широко используется при составлении чертежей, т.к. имеет ряд преимуществ перед центральным и косоугольным параллельным проецированием. К ним относятся простота геометрических построений ортогональных проекций точек и сохранение на проекциях, при определенных условиях, формы и размеров проецируемой фигуры.

3. Инвариантные свойства ортогонального проецирования

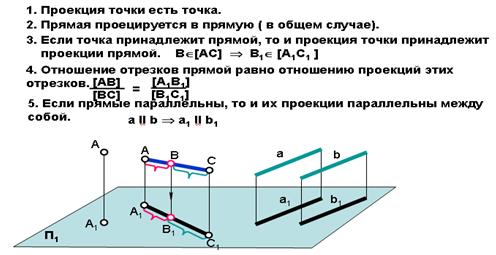
Обратимость чертежа

К чертежу предъявляются следующие требования: точность, простота, наглядность и обратимость.

Чертеж называется обратимым, если по изображению фигуры можно восстановить ее форму, размеры и положение в пространстве.

a1 º b1 ºc1

c

b

a

Обратимость чертежа может быть обеспечена проецированием на две (три) непараллельные плоскости проекций.

Метод Монжа

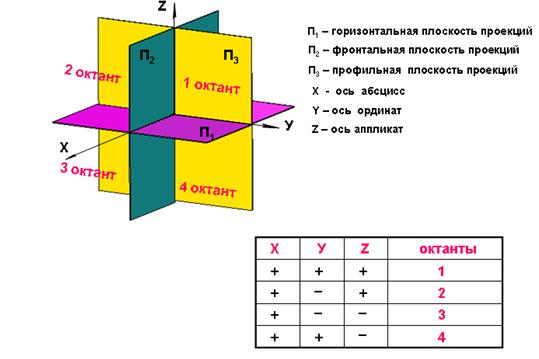
Французский математик и инженер Гаспар Монж предложил получать изображения путем ортогонального проецирования геометрического образа на несколько взаимно перпендикулярных плоскостей проекций (П₁,П₂, П₃).

Плоскости проекций пересекаясь, образуют восемь прямоугольных трехгранников (октант). (На рисунке показаны первые четыре октанта - четверти).

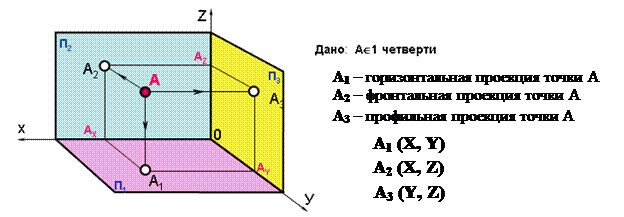
Наглядное изображение точки

Пусть дана точка А, принадлежащая первой четверти. Для того чтобы получить ортогональные проекции точки А, необходимо из этой точки опустить перпендикуляры на три плоскости проекций.

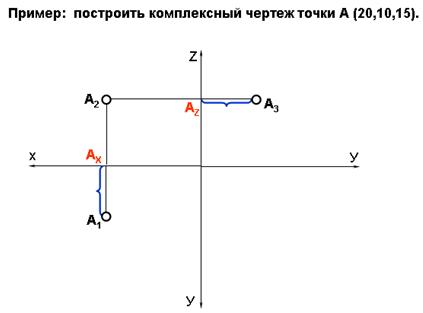
Комплексный чертеж

Совместим плоскость П₁ с плоскостью П₂ вращением вокруг оси ОХ, а плоскость П₃ с плоскостью П₂ вращением вокруг оси ОZ. Получим комплексный чертеж (эпюр).

А₂А₃ – горизонтальная линия проекционной связи

А₁А₂ – вертикальная линия проекционной связи

Для упрощения комплексного чертежа границы плоскостей проекций П₁,П₂,П₃ не указывают.

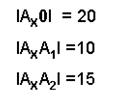Если все координаты точки имеют числовые значения, то точка расположена в пространстве. Если точка имеет одну нулевую координату, то точка принадлежит плоскости проекций.

Если точка имеет две нулевые координаты, то точка принадлежит оси проекций