Исследование функции с помощью первой производной

С помощью первой производной исследуется такие элементы поведения самой функции: возрастание, убывание, экстремум.

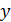
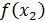
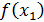
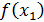
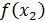
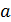
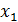
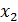
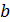
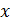
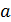
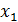
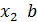
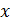
Рис.7

Определение. Функция 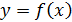называется возрастающей на некотором промежутке 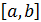, если для любых значений 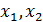этого промежутка из неравенства 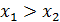, следует аналогичное неравенство для функции 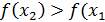) (правая часть рис. 7). Если из неравенства 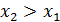следует противоположное неравенство для функции 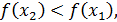то функция называется убивающей (левая часть рис. 7).

Возрастающие и убывающие функции объединяются одним термином -монотонные функции. Как часто бывает в математике, пользоваться определениями для решения практических задач весьма громоздко. Применим первые производные для исследования функций на монотонность.

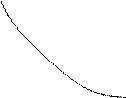
Геометрически нетрудно догадаться (рис. 7), что любая касательная к убывающей функции (левая часть рис. 7) образует с осью 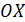тупой угол, следовательно 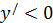; любая касательная к возрастающей функции образует острый угол с осью 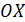, следовательно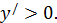

Нетрудно к этому результату прийти и аналитически. Возьмём любые две точки 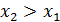, на промежутке 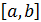и применим формулу Лагранжа:

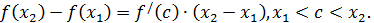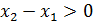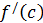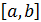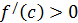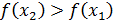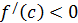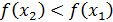Поскольку , то знак правой части равенства, следовательно, и левой части зависит от . Пусть на отрезке производная сохраняет свой знак. Если , то - функция возрастает, если , то - функция убывает.

Таким образом, справедлива теорема. Для того, чтобы дифференцируемая функция возрастала (убывала) на интервале 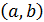, необходимо и достаточно, чтобы на этом интервале производная функции была положительной (отрицательной):

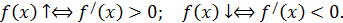
Определение. Функция 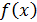имеет во внутренней точке 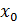отрезка 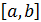максимум (минимум), если существует 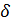- окрестность точки 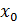, т.е. интервал 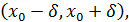во всех точках которого выполняется неравенство

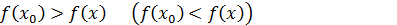(9)

На рис. 8 в точке 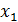функция имеет минимум, а в точке 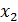- максимум.

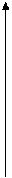Понятие максимума и минимума объединяется одним термином – экстремум.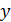

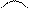
Рис.8

x

b

a

m

Заметим сразу, что экстремум является «локальным» понятием, т.е. определённым для точки и её малой окрестности. «Глобальным» понятием является наибольшее и наименьшее значения функции на отрезке 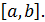Так, на рис. 8 наибольшее значение достигается в точке 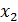- точке максимума, а наименьшее значение достигается в точке 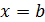- на правом конце отрезка.

Теорема (необходимый признак экстремума). Если функция 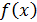дифференцируема в точке 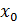и достигается в этой точке экстремума, то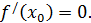

Доказательство следует из теоремы Ферма, применённой к окрестности 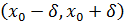, - ведь на этом интервале в точке 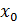функция имеет наибольшее или наименьшее значение.

Из рис. 8 видно, что в точке минимума 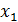производная существует и равна нулю (касательная параллельна оси 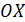), а в точке максимума 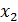производная не существует. Все возможные случаи изображены на рис. 9.

В точках 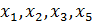производные равны нулю (касательные параллельны оси 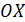); в точках 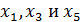функция имеет экстремум, а в точке 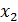экстремума нет.

+ - - +

- +

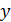
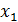
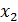
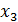
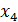
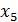
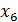
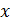
Рис.9

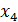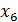В точках и производные не существуют, но в точке 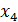имеется максимум, а в точке 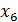экстремума нет.

Таким образом, точки, в которых производная равна или не существует, являются лишь «подозрительными» на экстремум. Они называются критическими (или стационарными) точками.

Теорема (1- й достаточный признак экстремума). Пусть функция 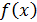непрерывна на некотором интервале и точка 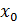внутри этого интервала является критической. Если при переходе через точку 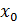производная меняет знак, то в этой точке функция имеет экстремум. При этом, если производная меняет знак с плюса на минус, то в точке 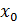имеется максимум; если с минуса на плюс, то минимум.

Доказательство очевидно благодаря связи знака производной с возрастанием и убыванием функции (см. рис. 9).

Пример 11. Исследовать на экстремум функцию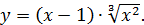

Решение. Сначала находим критические точки, т.е. «подозрительные» на экстремум. Для этого находим производную

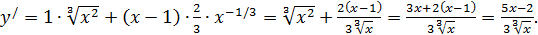
Имеются два источника критических точек.

1)

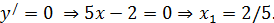
2) 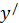не существует 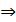знаменатель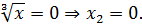

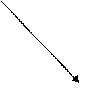Получили две критических точки. Эти точки разбивают числовую прямую на три интервала. Для выяснения знака производной на каждом интервале применим метод интервалов. Оформим это следующим образом:

+ +

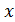
0

На интервалах 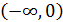и 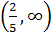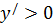, следовательно функция возрастает; на интервале 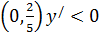, следовательно функция убывает. На рисунке это наглядно показано с помощью стрелок. Более того, стрелки полезны тем, что они как бы намечают эскиз графика функции. Сравните с графиком: функции, который изображён на рис. 10.

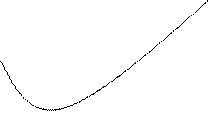
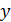
2/5

Рис.10

0 1

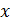
Теорема (2-й достаточный признак экстремума). Пусть функция 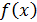непрерывна в окрестности критической точки 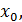причем 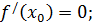существует 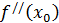, причём 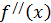непрерывна в окрестности точки 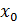. Тогда:

если 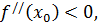то в точке 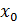имеется максимум,

если 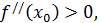то в точке 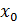имеется минимум,

если 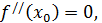то требуется дополнительное исследование. Доказательство. Воспользуемся разложением функции 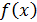по формуле Тейлора в окрестности точки 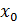в виде:

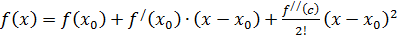(10)

где точка 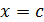находится между 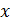и 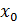. По условию теоремы мы рассматриваем тот случай критических точек, когда 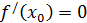, поэтому формула (10) приобретает вид:

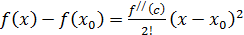(11)

Воспользуемся условиями теоремы, в котором говорится, что 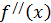непрерывна в окрестности точки 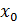. Это означает, что в этой окрестности 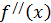сохраняет свой знак, т.е. тот, который она имеет в точке 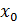. Отсюда следует: если 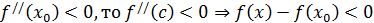, т.е. 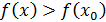-максимум; если 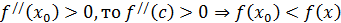– минимум.

Если 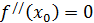, то в формуле Тейлора надо взять необходимое число слагаемых.

Замечание. Нетрудно заметить, что второй признак слабее первого: исследуются лишь те критические точки, для которых производная равна нулю и остаются без рассмотрения точки, в которых производная не существует.