Уравнения и системы уравнений в алгебре множеств
Для формализации процесса решения уравнений и систем уравнений в алгебре множеств введем дополнительные определения.
Пусть J - универс и A(1),A(2),...,A(n) - заданные множества этого универса, X - неизвестное множество. Обозначим через F[A(1),A(2),...,A(n),X] и R[A(1),A(2),...,A(n),X] две формулы алгебры множеств. Множество X* называется частным решением уравнения
F[A(1),A(2),...,A(n),X] = R[A(1),A(2),...,A(n),X], (1)
если F[A(1),A(2),...,A(n),X*] и R[A(1),A(2),...,A(n),X* ] определяют одно и то же множество.
Множество всех частных решений задает общее решениеуравнения (1).
Путем преобразования (используя законы алгебры множеств и следующие из них результаты) уравнение (1) может быть преобразовано к виду:
AX  B
B 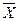
 C=
C=  . (2)
. (2)
Пусть задана система уравнений в алгебре множеств. Путем эквивалентных преобразований система уравнений так же может быть преобразована к виду (2). Отсюда, для решения уравнения или системы уравнений в алгебре множеств, необходимо уметь находить общее решение уравнения типа (2).
Основные леммы, используемые при решении уравнений в алгебре множеств.
Для преобразования уравнений и систем уравнений в алгебре множеств к виду:
AX  B
B 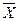
 C=
C=  , (1)
, (1)
а так же для нахождения общего решения уравнения (1), используются следующие результаты, получающиеся из законов алгебры множеств.
Лемма 1.
A B тогда и только тогда, если A
B тогда и только тогда, если A 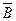 =
=  .
.
Доказательство.
Покажем, что из A B следует A
B следует A 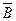 =
=  .
.
Доказательство от противного. Пусть A B, но A
B, но A 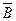
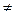
 . Отсюда существует такой элемент а, который одновременно принадлежит и множеству А и множеству
. Отсюда существует такой элемент а, который одновременно принадлежит и множеству А и множеству 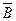 . Это означает, что этот элемент а принадлежит множеству А и не принадлежит множеству В, что противоречит условию A
. Это означает, что этот элемент а принадлежит множеству А и не принадлежит множеству В, что противоречит условию A B.
B.
Покажем, что из A 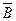 =
=  следует A
следует A B.
B.
Доказательство от противного. Пусть A 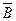 =
=  , но множество А не является подмножеством В. Тогда множество А содержит такой элемент а, которого нет в множестве В. Отсюда этот элемент принадлежит и множеству А и множеству
, но множество А не является подмножеством В. Тогда множество А содержит такой элемент а, которого нет в множестве В. Отсюда этот элемент принадлежит и множеству А и множеству 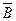 , что противоречит условию A
, что противоречит условию A 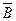
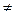
 .
.
Лемма доказана.
Лемма 2.
А=В тогда и только тогда, если А  В=
В=  .
.
Доказательство.
Покажем, что из А=В следует А  В=
В=  .
.
Если А=В, то А 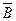 =А
=А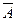 =
=  и В
и В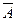 =В
=В 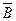 =
=  , отсюда А
, отсюда А  В=
В=  .
.
Покажем, что из А  В=
В=  следует А=В.
следует А=В.
Если А  В=
В=  , то это значит что А
, то это значит что А 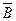 =
=  , т.е. по лемме 1 A
, т.е. по лемме 1 A B, и В
B, и В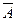 =
=  , т.е. по лемме 1 В
, т.е. по лемме 1 В А, Получили одновременно А
А, Получили одновременно А В и В
В и В  А, что соответствует А=В.
А, что соответствует А=В.
Лемма доказана.
Лемма 3.
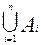 =
=  , тогда и только тогда, если
, тогда и только тогда, если 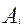 =
=  , i=1,2,...,n.
, i=1,2,...,n.
Доказательство индукцией по n.
Лемма 4.
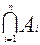 =J, тогда и только тогда, если
=J, тогда и только тогда, если 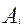 =J, i=1,2,...,n.
=J, i=1,2,...,n.
Доказательство следует из леммы 3 на основании принципа двойственности.
Полученные теоретические результаты позволяют находить общее решение уравнений и систем уравнений.
Рассмотрим уравнение
F[A(1),A(2),...,A(n),X] = R[A(1),A(2),...,A(n),X] (1)
относительно неизвестного множества X.
Из леммы 1 следует, что уравнение (1) эквивалентно уравнению
F[A(1),A(2),...,A(n),X]  R[A(1),A(2),...,A(n),X]=
R[A(1),A(2),...,A(n),X]=  . (2)
. (2)
После преобразований (применив, если это надо, закон де Моргана и другие законы алгебры множеств; на основании ассоциативного и дистрибутивного законов раскрыв скобки и приведя подобные члены) уравнение (2) становится эквивалентным уравнению
AX  B
B 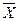
 C=
C=  , (3)
, (3)
где А,В и С - некоторые множества, полученные в результате проведенных преобразований.
Из (3) по лемме 3 следует, что AX=  , B
, B 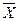 =
=  , C=
, C=  .
.
Из того, что AX=  и B
и B 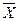 =
=  , по лемме 1 следует:
, по лемме 1 следует:
В  X
X 
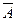 .
.
Отсюда, уравнение (3) эквивалентно условиям :
В  X
X 
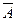 ,C=
,C=  . (4)
. (4)
Так как X произвольное множество из универса, то из (3) следует, что условия :
В 
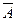 ,C=
,C=  (5)
(5)
являются необходимыми и достаточными для того, чтобы исходное уравнение (1) имело решение.
Вместо условий (5) можно пользоваться эквивалентными им (на основании лемм1 и 3) условиями :
АВ  C=
C=  . (6)
. (6)
Мы получили, что любое множество X* из универса, удовлетворяющее условиям (4), является частным решением уравнения (1).
Из условий (4) следует, что решение исходного уравнения (1) определяется следующим выражением:
X*= В  К
К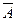 ,(7)
,(7)
где К - произвольное множество универса.
Таким образом, мы получили, что при любом К из универса выражение (7) представляет собой частное решение исходного уравнения (1), т.е. (7) определяет общее решение исходного уравнения (1). Из выражения (7) следует и оценка числа решений уравнения (1) N= 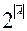 . Проверим полученное решение. Так как X* решение системы (1), то оно является и решением преобразованного уравнения (2). Подставив в уравнение (2) выражение для X* из (7), получим:
. Проверим полученное решение. Так как X* решение системы (1), то оно является и решением преобразованного уравнения (2). Подставив в уравнение (2) выражение для X* из (7), получим:
A(В  К
К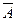 )
)  B(
B(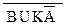 )
)  C=AB
C=AB  B(
B( 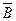
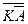 )
)  C=AB
C=AB  C=
C=  .
.
Здесь последнее равенство следует из условий (6).
Замечание.
Так как система уравнений алгебры множеств может быть приведена на основании выше доказанных лемм к виду (3), то результаты, полученные для случая решения уравнения, справедливы и для случая решения системы уравнений.
