Лекция 1: «Множество. Алгебра множеств»
Федеральное агентство по образованию российской федерации
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ЭКСПЕриментальная лаборатория министерства
образования и науки российской академии образования
КРАСНОГОРСКИЙ ОПТИКО-ЭЛЕКТРОННЫЙ КОЛЛЕДЖ

В.Р.Нелюбин
КУРС ЛЕКЦИЙ
по дисциплине “Дискретная математика”
| Одобрены предметной (цикловой) комиссией (кафедрой) гуманитарных и социально-правовых дисциплин /протокол № __________ от ___________________/ Председатель комиссии (заведующий кафедрой) ___________С.Р.Гуриков | Составлены в соответствии с Государственными требованиями к минимуму содержания и уровню подготовки выпускника Заместитель директора по учебной работе __________________ Т. П. Дубровская |
В.Р.Нелюбин
КУРС ЛЕКЦИЙ
по дисциплине “Дискретная математика”
Для студентов специальности
«Программное обеспечение вычислительной техники и автоматизированных систем»
Рассмотрено и утверждено на заседании кафедры специальности “Программное обеспечение вычислительной техники и автоматизированных систем”
Автор: Нелюбин В.Р. Курс лекций по дисциплине “Дискретная математика”
.
Издание предназначено для студентов специальности «Программное обеспечение вычислительной техники и автоматизированных систем», в котором без излишней детализации (без приведения доказательств теорем и выводов громоздких формул) рассмотрен весь комплекс знаний по дисциплине “Дискретная математика” для решения математических задач вручную и с использованием электронно-вычислительной техники.
Рецензент: Орешкина Л.В. – декан Красногорского ОЭК, кандидат педагогических наук
©Красногорский оптико-электронный колледж, 2007 г.
©Нелюбин В.Р.
От автора
Настоящая книга рекомендована студентам специальности «Программное обеспечение вычислительной техники и автоматизированных систем», изучающих дисциплину “Дискретная математика”.
Назначение этой книги – настольная тетрадь студента (конспект). Эта книга освобождает студента от необходимости записывать (или переписывать у товарища) лекции, совершая при этом множество ошибок. Тем самым у студента высвободится нерационально используемое время для осмысления текста и решения задач. Получив эту книгу в электронном виде, студенту рекомендуется распечатать и сброшюровать её таким образом, чтобы текст был только на левой части разворота, а правая часть будет использована студентом для пометок студента на занятиях (ответы на возникшие вопросы, решение задач и т.д.). В книге выделены ключевые слова, которые будут использованы преподавателем для проведения компьютерного тестирования студентов, для определения степени усвоения материала. Оценивание студентов предусмотрено после прохождения каждого раздела дисциплины путём компьютерного тестирования (списки контрольных вопросов приведены в настоящей книге в конце каждого учебного раздела), а также проведением контрольных работ по решению практических задач (примеры контрольных задач также приведены в настоящей книге). Желаю успехов в освоении дисциплины “Дискретная математика”.
Автор будет признателен всем пользователям (студентам и преподавателям) за сообщения об ошибках, выявленных в настоящей книге. Мой E-MAIL: [email protected].
СОДЕРЖАНИЕ
| Введение | |
| Лекция 1. «Множество. Алгебра множеств» | |
| Лекция 2. Теория булевых функций. Булева алгебра. | |
| Лекция 3. Определение и способ задания булевых функций | |
| Лекция 4. Дизъюнктивные нормальные формы (ДНФ). Конъюнктивные нормальные формы (КНФ) | |
| Лекция 5. Продолжение темы «ДНФ» | |
| Лекция 6. Метод Квайна – Мак-Клоски для нахождения минимальной ДНФ | |
| Лекция 7. Функционально полные системы функций | |
| Лекция 8. Продолжение темы «Многочлены Жегалкина» | |
| Лекция 9. Продолжение темы «Классы функций» | |
| Лекция 10. Функциональные элементы. Логические схемы | |
| Лекция 11. Графы | |
| Лекция 12. Эйлеровы графы | |
| Лекция 13. Сети. Пути в орграфах. Остовы минимальной длины | |
| Лекция 14. Парное сочетание (паросочетание) двудольных графов | |
| Лекция 15. Потоки в транспортных сетях | |
| Лекция 16. «Системы счисления» | |
| Лекция 17. «Модулярная арифметика» | |
| Лекция 18. «Теория шифрования» |
ВВЕДЕНИЕ
Учебная дисциплина “Дискретная математика” предназначена для реализации государственных требований к содержанию и уровню подготовки выпускников по специальности “Программное обеспечение вычислительной техники и автоматизированных систем” для колледжа.
Преподавание данного курса имеет практическую направленность и проводится в тесной взаимосвязи с другими общепрофессиональными дисциплинами. Использование межпредметных связей обеспечивает преемственность изучения материала.
Материал данного предмета используется при изучении дисциплин “Математика и информатика”, “Математическая статистика”, “Архитектура ЭВМ, систем и сетей”, “Основы алгоритмизации и программирование”, “Базы данных”, “Автоматизированные системы”, “Технология разработки программных продуктов”, “Компьютерное моделирование”.
Рабочей программой дисциплины предусматривается изучение:
· основ теории множеств;
· систем счисления и модулярной арифметики;
· основ теории графов;
· основ комбинаторики;
· основ алгебры логики.
В результате изучения дисциплины студент должен:
иметь представление:
· о значении и областях применения данной дисциплины:
знать:
· основы теории множеств;
· аппарат формул логики и теорию булевых функций;
· способы минимизации логической схемотехники;
· основы алгебры вычетов;
· методологию шифрования;
· метод математической индукции;
· основные формулы комбинаторики;
· основы теории графов;
уметь:
· выполнять операции над множествами, применять аппарат теории множеств для решения задач;
· строить таблицы истинности для формул логики и упрощать формулы логики;
· представлять булевы функции в виде форму заданного типа, определять возможность выражения одних булевых функций через другие;
· исследовать бинарные отношения на заданные свойства;
· выполнять операции в алгебре вычетов;
· применять простейшие шифры для шифрования текстов;
· доказывать утверждения с помощью метода математической индукции;
· генерировать основные комбинаторные объекты;
· находить характеристики графов, выделять структурные особенности графов, исследовать графы на заданные свойства, применять аппарат теории графов для решения прикладных задач;
· строить автоматы с заданными свойствами.
Базовыми дисциплинами для изучения предмета “Дискретная математика” являются “Математика” и “Информатика”.
Рабочая программа учебной дисциплины на 90 часа аудиторных занятий, в том числе 24 часа отводится на практические занятия.
Лекция 1: «Множество. Алгебра множеств»
Введем обозначения:
N (или ω) –множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
R – множество действительных (вещественных) чисел;
С – множество комплексных чисел.
X 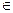 R – элемент X принадлежит множеству R.
R – элемент X принадлежит множеству R.
Равные множества – множества, состоящие из одинаковых элементов.
A = B – множество А равно множеству B.
Ø – пустое множество.
A 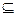 C – Множество А является подмножеством множества С.
C – Множество А является подмножеством множества С.
Если A 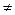 C и A
C и A 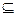 C, то A
C, то A 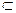 C (строго).
C (строго).
Если A 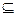 C и C
C и C 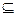 A, то A = С.
A, то A = С.
Пустое множество Ø является подмножеством любого множества.
Универсальное множество (универсум) U содержит в себе все множества и любое множество является подмножеством универсального множества.
Можно записать следующее: Ø 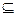 N
N 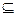 Z
Z 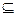 Q
Q 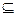 R
R 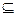 C
C 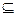 U.
U.
Множества A и B называются эквивалентными (обозначается A~B), если 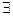 биекция f: A↔B (или по другому y=f(x) и x=f(y), при y
биекция f: A↔B (или по другому y=f(x) и x=f(y), при y 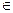 A и x
A и x 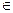 B).
B).
Мощностью множества A называется класс всех множеств, эквивалентных множеству A (обозначается 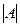 ).
).
Существуют конечные и бесконечные множества. Пусть множество A состоит из n элементов. Это множество называется конечным. Число n называется мощностью данного множества. 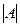 =n.
=n.
Множество натуральных чисел мощность является счетным (т.е. все элементы можно пронумеровать). Если A~N, то мощность 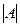 =N.
=N.
Если A~ 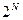 , т.е. A={1,2,4,8,…,
, т.е. A={1,2,4,8,…, 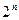 ,…}, то множество A называется континуальным (или континуумом). Мощность
,…}, то множество A называется континуальным (или континуумом). Мощность 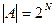 .
.
