Сыныптар үшін «Математиканың таңдамалы мәселелері» тақырыбында таңдау (электив) курсы

Оқушылардың бейімділік дайындығынан алдын бейімдіктен алдыңғы дайындық негізгі мектептің 9-сыныптан бері жүргізіледі. Бұл арнайы таңдау курстары арқылы жүзеге асырылады.

Ол үшін 2-4 (6-8)сабаққа арналған мектеп математика курсына қатысты тақырыптар таңдап алынады.

Бұл тақырыптардың әрқайсысын жеке-жеке алғанда және олардың тұтастай барлығы оқушылардың математка пәніне қызығушылығын арттыруын, математиканың негізгі идеялары және әдістерімен таныстыру көзделеді. Ең негізгісі, қызықты есептер шығару болып табылады.

Ресейде XI сыныптарда мынадай тақырыптарды оқу қарастырылған:

1. Комбинаторикамен танысу;
2. Өмірде кездесетін проценттік есептер;
3. Алтын қима;
4. Шифрлау және математика;
5. Диафонт теңдеулері;
6. Квардрат функцияның қасиеттерін пайдалану;
7. Координат жазықтығындағы екі белгісізі бар теңсіздіктер;
8. Модульмен берілген теңдеулердің графиктері;
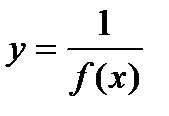9. түріндегі функцияның графигі;
10. Санның бүтін және бөлшек бөлігі;
11. Орта туралы теоремалардың геометрялық дәлелдемесі;
12. Формула бойынша кесіндіні салу;
13. Тек циркульдің жәрдемімен салу;

Әрбір тақырыпқа әдістемелік талдау берілген, онда

• Тақырыптың мазмұны көрсетіледі. Сабақтың тақырыптық жоспары;
• Түсініктемелік материал. Әдістемелік ұсыныстар;
• Есептер шығару үлгілері. Мұғалімдерге арналған кеңестер;
• Өз бетінше шығаратын есептер;

Бұл тақырыптардың барлығы да ІX сынып оқушылырының шама-шарқына лайықты және ол материалдарды игеру үшін базалық білім жеткілікті екендігін тәжірибе көрсетті. Ұсынылып отырған тақырыптардың қиындық дәрежесі математикадан білімі жоғары оқушылар ғана емес басқа да математикадан әзірше қабілеті белгілі бола қоймаған оқушыларды тартуға және олардың математикаға қызығушылығын арттыруға мүмкіндік береді.

Таңдау тақырыптары курсы оқушыларда әдейі арналған біліктілік пен дағдыларды қалыптастыруды мақсат етіп қоймайды. Бірақ курсты толығымен қарастыру оқушылардың дайындық дәрежесіне игі ықпал етеді.

«Математиканың таңдамалы мәселелері» атты таңдау курсының мынадай ерекшеліктері бар:

1. Тақырыптарды оқу ретін мұғалім өз бетінше өзгертіп оқытуға да, барлығын түгел қарастырмауға да болады.

2. Мұғалім оқушылардың қызығу дәрежесіне байланысты басқа тақырыпты таңдауға қақылы.

3. Бұл тақырыптар бірінен бірі туындамайды (бір-біріне тәуелсіз) сондықтан, оқушылар бұл таңдау курсына кез-келген уақытта келіп қосылуға болады.

4. Бұл тақырыптар көлемі жағынан үлкен болмауы, бірақ қызықты болуы мүмкін.

Ескерте кететін маңызды бір мәселе: курстың материалдары мен сәйкес есептері бақылау жұмыстарына және емтиханға енгізілмейді.

Таңдау тақырыптары(4 сағ.)

1.Комбинаторикамен танысу.

2.Өмірде кездесетін проценттік есептеулер.

Негізгі мазмұны

· Сату-сатып алу (распродажа).

· Баға (тариф).

· Айып пұл (штраф).

· Банк операциялары.

· Дауыс беру.

3.Алтын қима (2 сағ.).

Негізгі мақсаты – жалпы білімділік: алтын қимамен таныстыру оқушының жалпы ой өрісін арттырады, математикалық деректердің эстетикалық қабылдауын дамытады, математиканың қолданудағы әртүрлі жағдайларымен таныстыруға мүмкіндік береді.

Негізгі мазмұны

· «Алтын қима» сөзі.

· Алтын қима неге тең?

· Циркуль және сызғыштың жәрдемімен алтын тік төртбұрыш салу.

· Қызықты дерек: алтын тік төртбұрыш пішінін сақтайды.

· Бес бұрышты жұлдыз адамдардың көңілін неге өзіне ерекше аударған?

4.Паскаль үшбұрышы (2 сағ.).

· Паскаль үшбұрышы деген не және оны қалай құруға болады?

· Паскаль ушбұрышының кейбір қасиеттері.

· Символдық белгілеулер енгізу. Паскаль үшбұрышының рекурентті формуламен берілуі.

· Паскаль үшбұрышы және екімүшені дәрежелеу.

5.Шифрлау және математика.

Негізгі мазмұны

· Есептің берілуі.

· Шифрлаудың матрицалық тәсілі.

· Есептің шығарылуы.

· Матрицаның алгебрасы туралы қысқаша әңгіме.

6.Диафонт теңдеулері (2 сағ.).

Негізгі мазмұны

· Кіріспе есеп және тарихи шолу.

· «Перебор» әдісі арқылы сызықты теңдеулерді шешу.

· «Спуск» әдісі арқылы шығарылатын есептің мысалдары.

· Бүтін коэфицентті сызықты теңдеудің әр уақытта бүтін шешімі бола ма?

· Бүтін сандар жиынында шешілетін екінші дәрежелі теңдеу (Пифогор саны туралы есеп).

7.Квардрат функцияның қасиеттерін пайдалану (2 сағ.).

Негізгі мазмұны

· Квадрат үшмүшенің түбірлерінің таңбалары.

· Квадрат үшмүшенің қасиеттерін есептер шығаруда қолдану.

· Өз бетінше шығаруға берілген есептер.

8.Координат жазықтығындағы екі белгісізі бар теңсіздіктер.

Негізгі мазмұны

· Координат жазықтығында 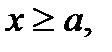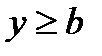теңсіздігінен және олардың жүйесімен берілген облыстың берілуі

;

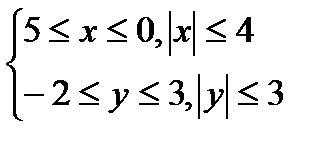· Екі белгісізі бар теңсіздік және олардың жүйесімен берілген облыс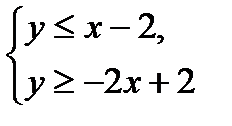

· Сызықтық емес екі айнымалысы бар теңсіздіктер мен олардың жүйесінің геометриялық интерпрециясы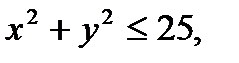

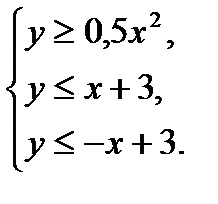
9.Модулі бар теңдеулердің графигі (4 сағ.).

Модулі бар теңдеулердің графигін салу. Бұл теңдеудің эстетикалық мәніне көңіл аудару, оқушылардың шығармашылық мүмкіндігін қайта қарау.

Негізгі мазмұны

· Дайындық кезеңі – базалық білім-біліктерді қайта жаңғырту.

· Мысалдар арқылы функцияның графигін салу тәсілдерін көрсету және жаттығулар орындау.

10. 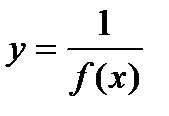функциясының графигі (2 сағ.).

Негізгі мазмұны

· Дайындау кезеңі: мақсат қою және базалық білімдерін тексеру.

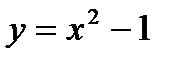· және 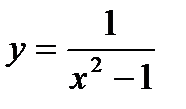функцияларының графиктері арқылы түсіндіру.

· Жаттығулар.

· Дайын графиктен тапсырмалар орындау.

Әдебиеттер:

1.Гельфанд И.М., Глаголева Е.Г., Шноев Э.Э. Функции и графики. – М.:Наука, 1965.

2.Гончаров В.Л. Элементарные функции действительного переменного/Энциклопедия элементарной математики Т.З. – М.- Л.: Гостехиздат.,1954.

11.Санның бүтін және бөлшек бөлігі (2сағ.).

Негізгі мазмұны

· Санның бүтін және бөлшек бөлігінің анықтамасы.

· «Санның бүтін бөлігі» функциясының графигі.

· «Санның бөлшек бөлігі» функциясының графигі.

· Есеп шығару.

12.Орта туралы теоремалардың геометриялық дәлелдемесі (4сағ.).

Негізгі мақсат – оқушылардың шамалардың ортасы туралы түсініктерін кеңейту. Гармониялық орта - 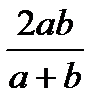, екі оң санның орта квадраты - 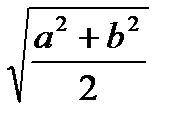таныстыру және геометриялық әдісті пайдаланып

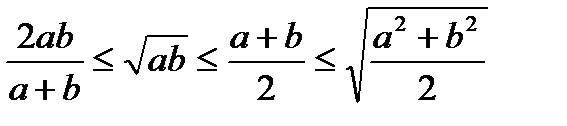теңсіздігін дәлелдеу.

Бұл материалдар мектеп математкика курсында кең таралмағанымен ол оқушылардың шама-шарқына, білім дәрежесіне лайық, қызықты. Алгебра мен геометрияның байланысын ашуға мүмкіндік береді.

Негізгі мазмұны

· Тарихи шолу.

· Арифметикалық, геометриялық, гармониялық, квадраттық орталар.

· Орта туралы теоремаларды дәлелдеу.

Әдістемелік нұсқау.

Орталарды салыстыру проблемасымен ғалымдар өте ерте заманнан бастап шұғылданған.