Основные теоремы о пределах

Теорема 1. (о предельном переходе в равенстве)Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.

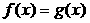Þ .

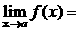
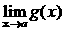Теорема 2. (о предельном переходе в неравенстве)Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).

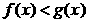Þ .

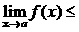
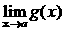Теорема 3. Предел постоянной равен самой постоянной.

.

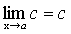Доказательство. f(x)=с, докажем, что .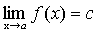

Возьмем произвольное e>0. В качестве d можно взять любое

положительное число. Тогда при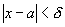

.

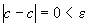Теорема 4. Функция не может иметь двух различных пределов в

одной точке.

Доказательство. Предположим противное. Пусть

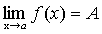и .

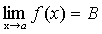По теореме о связи предела и бесконечно малой функции:

f(x)-A= 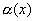- б.м. при ,

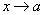f(x)-B= 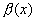- б.м. при .

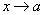Вычитая эти равенства, получим: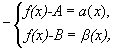

B-A= - .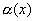

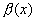Переходя к пределам в обеих частях равенства при 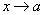, имеем:

B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.

Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при 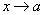, то и алгебраическая сумма имеет предел при 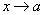, причем предел алгебраической суммы равен алгебраической сумме пределов.

.

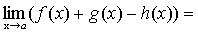
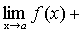
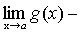
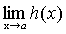Доказательство. Пусть , , .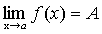

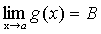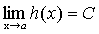Тогда, по теореме о связи предела и б.м. функции:

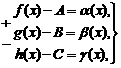где 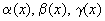- б.м. при .

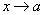Сложим алгебраически эти равенства:

f(x)+g(x)-h(x)-(А+В-С)= ,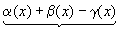

где 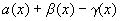б.м. при .

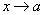По теореме о связи предела и б.м. функции:

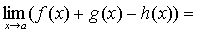А+В-С= .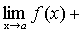

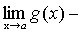
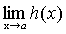Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при 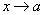, то и произведение имеет предел при 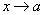, причем предел произведения равен произведению пределов.

.

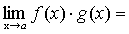
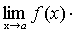
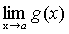Следствие. Постоянный множитель можно выносить за знак предела.

.

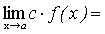
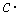
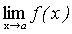Теорема 7. Если функции f(x) и g(x) имеют предел при ,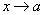

причем 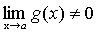, то и их частное имеет предел при 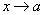, причем предел частного равен частному пределов.

, .

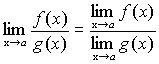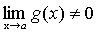37.

Первый замечательный предел имеет вид: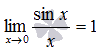

На практике чаще встречаются модификации первого замечательного предела в виде

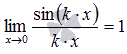
где, k – коэффициент.

Пояснение:

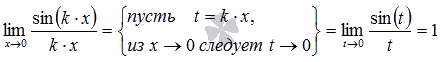
Следствия первого замечательного предела:

1.

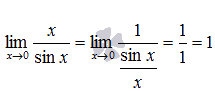
2.

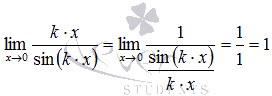
Эти следствия очень просто доказываются, если использовать правило Лопиталя или заменуэквивалентных бесконечно малых функций.

Разберем несколько примеров нахождения предела по первому замечательному пределу сподробным оприсанием решения.

Пример.

Найти предел не пользуясь правилом Лопиталя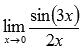

Решение.

Подставляем значение:

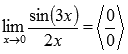
Пришли к неопределенности ноль делить на ноль. Смотрим в таблицу неопределенностей для определения метода решения. Комбинация синуса и его аргумента подсказывает нам о применении первого замечательного предела, но для этого сначала нужно немного преобразовать выражение. Домножим на 3х и числитель и знаменатель дроби.

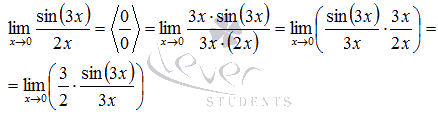
В силу следствия из первого замечательного предела 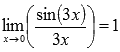, поэтому приходим к результату:

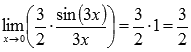
Ответ:

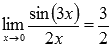
Пример.

Вычислить предел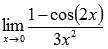

Решение.

Подставляем значение:

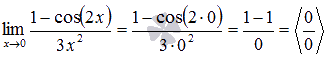
Пришли к неопределенности ноль делить на ноль. Преобразуем числитель, используя формулы тригонометрии.

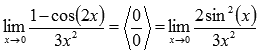
Стало видно, что здесь можно применить первый замечательный предел:

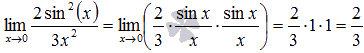
Ответ:

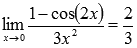
Пример.

Вычислить предел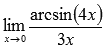

Решение.

Подставляем значение:

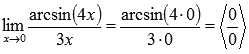
Пришли к неопределенности ноль делить на ноль. Сделаем замену.

Пусть

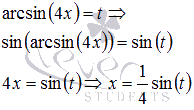
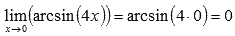, следовательно, 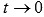при .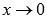

Тогда предел после замены переменной примет вид:

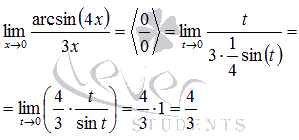
Ответ:

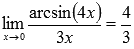
38.