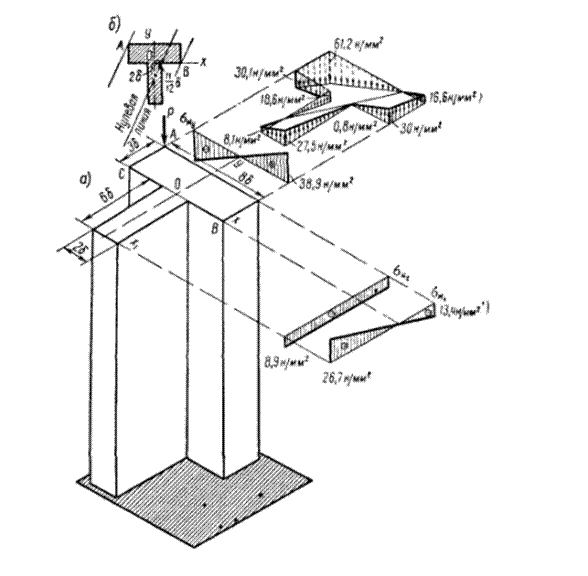
Пример расчетов задач по теме «плоский изгиб с растяжением - сжатием»

Совместное действие изгиба и растяжения (сжатия)

При сочетании прямого изгиба и растяжения (или сжатия) бруса в его поперечных сечениях возникает три внутренних силовых фактора: Продольная сила N_x, поперечная сила Q_y (или Q_z), изгибающий момент M_z (или M_y). Этот случай нагружения изображен на рисунке, и показаны эпюры нормальных напряжений σ_N2 и σ_My для некоторого произвольного сечения, находящегося на расстоянии a от свободного конца.

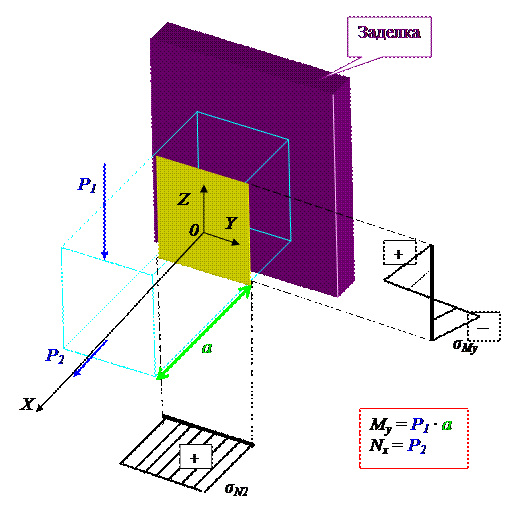
Этот случай нагружения практически почти не отличается от частного случая внецентренного растяжения, который сводится к центральному растяжению и чистому прямому изгибу.

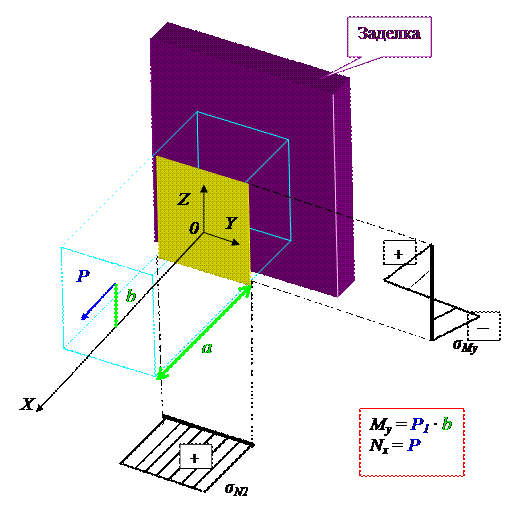
Отличие состоит в том, что в первом случае во всех поперечных сечениях Q_z = 0 и, следовательно, изгибающий момент во всех поперечных сечениях имеет одно и то же значение. Учитывая, что и N_x во всех поперечных сечениях одинакова, приходим к заключению, что все поперечные сечения равноопасны.

В обоих рассмотренных случаях нормальное напряжение в произвольной точке поперечного сечения вычисляется как алгебраическая сумма напряжений, соответствующих продольной силе и изгибающему моменту:

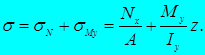
При сочетании косого изгиба и осевого нагружения бруса в его поперечных сечениях возникает пять внутренних силовых факторов N_x, Q_y, Q_z, M_y, M_z.

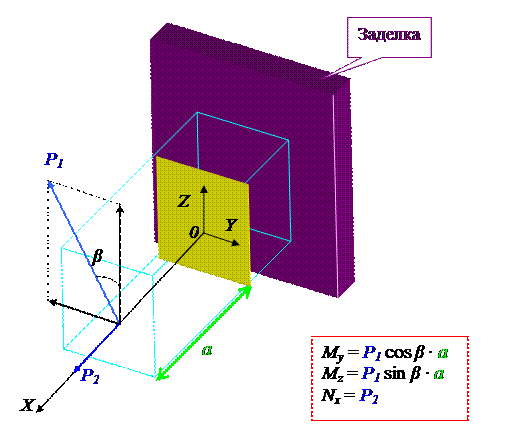
К сочетанию чистого косого изгиба с центральным растяжением сводится общий случай внецентренного растяжения бруса.

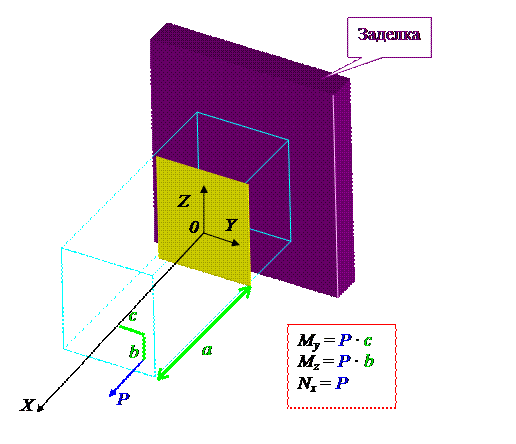
Нормальное напряжение в двух последних случаях в произвольной точке поперечного сечения вычисляется по формуле:

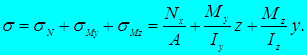
Знак каждого из слагаемых целесообразно устанавливать по характеру деформации бруса.

Необходимо иметь в виду, что вычисление напряжений, основанное на принципе независимости действия сил, допустимо лишь для достаточно жесткого бруса. Только в этом случае перемещения, возникающие вследствие упругих деформаций, настолько малы, что можно не учитывать их влияния на расположение нагрузок, т.е. вести расчет, исходя из размеров недеформированного бруса.

Пример расчетов задач по теме «плоский изгиб с растяжением - сжатием»

Задача 10.

Для заданной балки требуется:

1) изобразить расчетную схему и построить эпюры продольных сил N и изгибающих моментов M;

2) определить положение нейтральной линии в опасном сечении;

3) построить эпюры нормальных напряжений в опасном сечении от продольной силы, изгибающего момента и их совместного действия (суммарную эпюру σ).

Примечание. Плоскость действия нагрузки совпадает с плоскостью симметрии стержня.

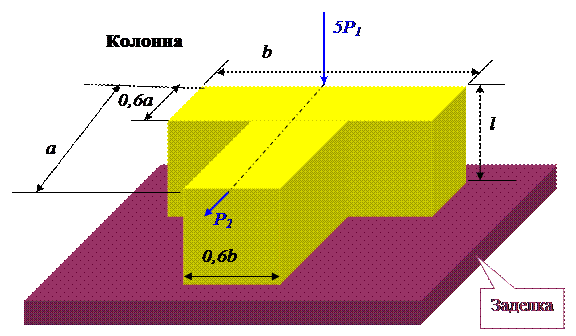
a = 0,34 м; P₁ = 510 кН; двутавр № 36;

b = 0,40 м; P₂ = 34 кН; швеллер № 18 a;

c = 3,2 м; q = 16 кН/м; уголок 200х200х20.

1) Изобразим расчетную схему и построим эпюры продольных сил N и изгибающих моментов M.

а) Вычислим величины на чертеже.

5P₁ = 5 ∙ 510 = 2550 кН;

0,6a = 0,6 ∙ 0,34 = 20,4 см;

0,4a = 0,4 ∙ 0,34 = 13,6 см;

0,6b = 0,6 ∙ 40 = 24 см.

б) Отметим точки A, B, D, E на чертеже:

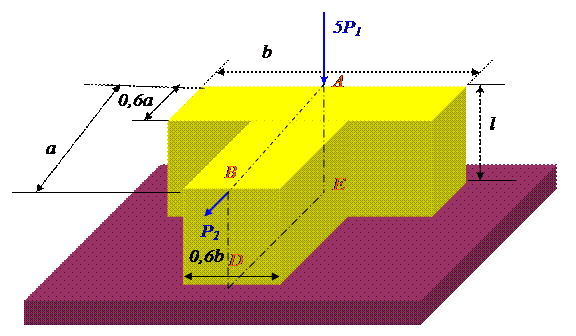
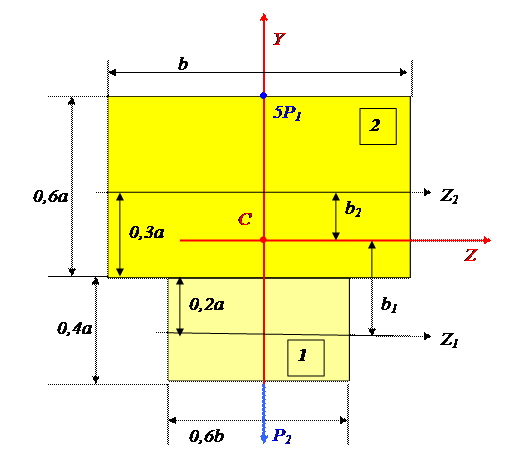
Колонна имеет сечение в виде тавра, состоящего из двух простых фигур – двух прямоугольников 1 и 2. Сечение симметричное, проведем центральную ось Y.

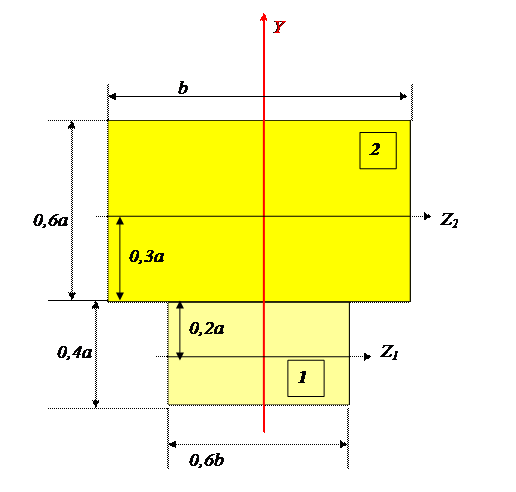
в) Вычислим геометрические характеристики.

Площади фигур:

A₁ = 0,6b ∙ 0,4a = 24 ∙ 3,6 = 326,4 см²;

A₂ = 0,6a ∙ b = 20,4 ∙ 40 = 816 см²;

A = A₁ + A₂ = 326,4 + 816 = 2142,4 см².

Положение центра тяжести (в качестве отсчета, т.е. в качестве вспомогательной оси принята ось Z₁):

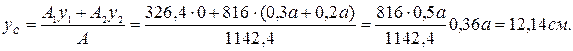
Проведем центральную ось Z. Расстояние между осями Z₁ и Z₂ простых фигур и центральной осью определим из чертежа.

b₁ = 12,14 см;

b₂ = (0,5a – b₁) = 4,86 см.

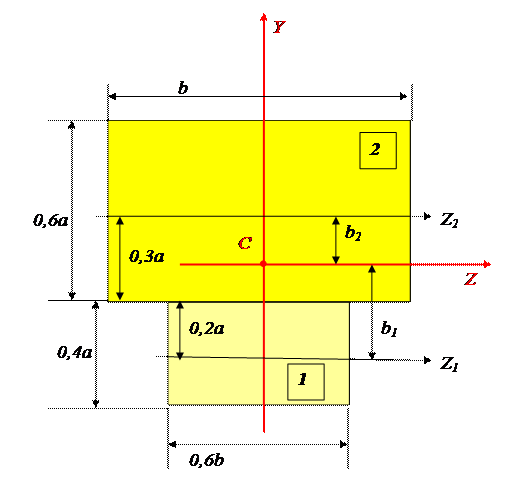
Моменты инерции относительно центральных осей:

I_Z = (I_Z1 + b₁² ∙ A₁) + (I_Z2 + b₂² ∙ A₂);

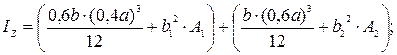
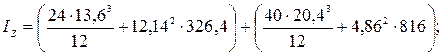
I_Z = (5030,9 + 48104,7) + (28298,9 + 19273,6) = 100708,1 см⁴.

В этом варианте задачи достаточно знать I_Z, но в общем случае надо искать I_Z и I_Y.

I_Y = I_Y1 + I_Y2 = 0.4a ∙ (0,6b)³ + 0.6a ∙ b³ = 0.4 ∙ 34 ∙ 24³ + 20,4 ∙ 40³;

I_Y = 188 006,4 + 1 305 600 = 1 493 606,4 см⁴.

Квадраты радиусов инерции сечения:

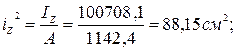
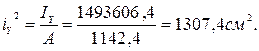
Координаты точки приложения силы 5P₁:

z_5P1 = 0; y_5P1 = b₂ + 0,3a = 4,86 + 0,3 ∙ 34 = 15,06 см.

Координаты точки приложения силы P₂:

z_P2 = 0; y_P2 = – (b₁ + 0,2a) = – (12,14 + 0,2 ∙ 34) = – 18,94 см.

г)Расчетная схема – это упрощенное изображение (схематизация) объекта, где не учитывается ряд второстепенных факторов, оказывающих несущественное влияние на результат расчета.

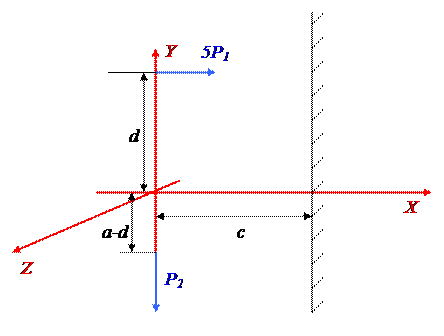
d = 0,8a – y_C = 0,8a – 0,36a = 0,44a = 0,44 ∙ 34 = 14,96 см.

Изобразим расчетную схему:

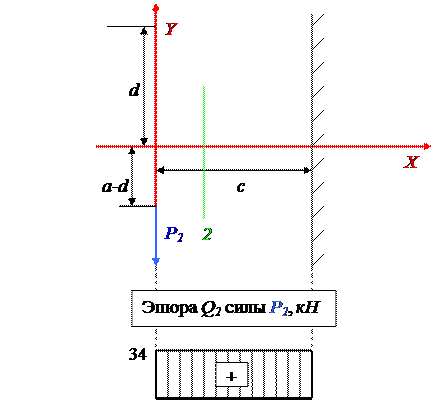
д) Построим эпюру Q₂ силы P₂. В сечении 2 внутри колонны Q₂ = P₂ = 34 кН.

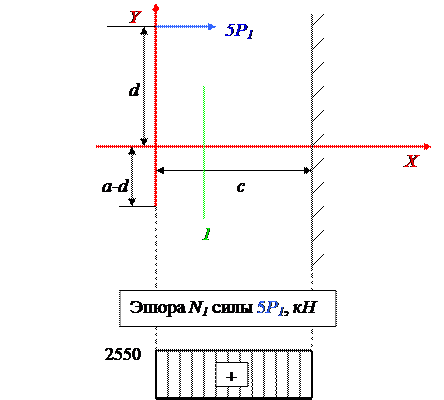
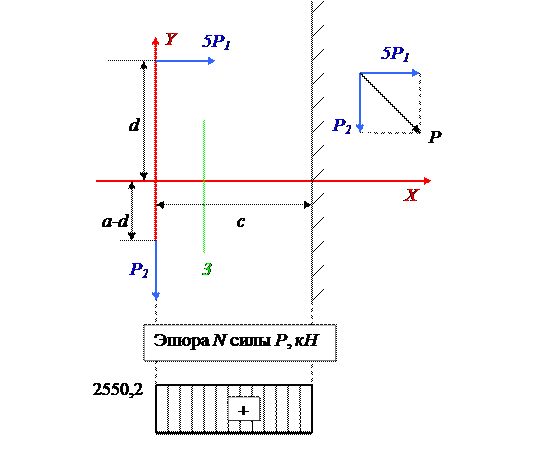
Построим эпюру N₁ силы 5P₁. В сечении 1 внутри колонны N₁ = P₂ = 34 кН.

Построим эпюру N результирующей силы.

N = P = 34 кН.

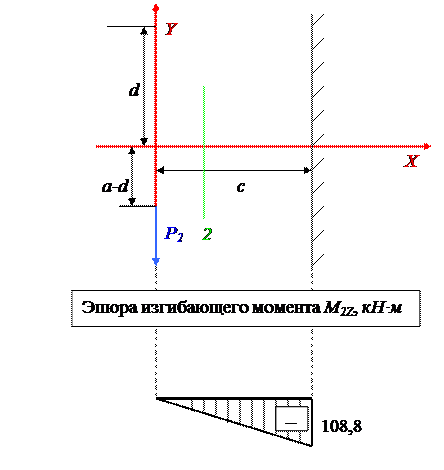
Построим эпюру изгибающего момента M_2Z силы P₂.

M₂ = P₂ ∙ c = 34 ∙ 3,2 = 108,8 кН·м; M₂ < 0.

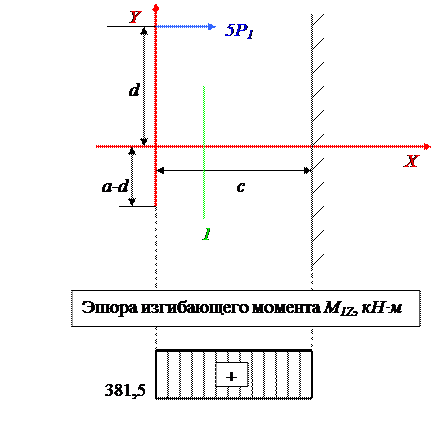
Построим эпюру изгибающего момента M_1Z силы 5P₁.

M₂ = 5P₁ ∙ d = 2550 ∙ 14,96 ∙ 10^-2 = 38148 ∙ 10^-2 = 381,5 кН·м.

2) Определим положение нейтральной линии в опасном сечении.

Из эпюр видно, что опасным сечением является сечение в области заделки. Максимальное сжатие в точке E, максимальное растяжение в точке D. Результирующий момент в опасном сечении

M_Z = M_1Z – M_2Z = 381,5 – 108,8 =272,7 кН·м.

Запишем уравнение нейтральной линии

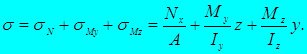
Нейтральная линия не проходит через центр тяжести и представляет собой прямую, отсекающую на осях координат отрезки

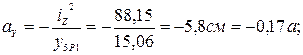
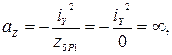
ð прямая не пересекает ось Z, она параллельна оси Z.

Проведем нейтральную линию в опасном сечении.

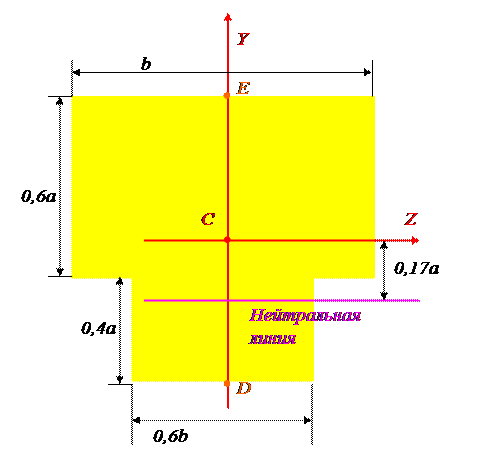
Найдем напряжение сжатия в опасной точке E:

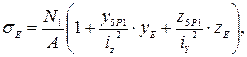
y_E и z_E – координаты точки E.

z_E = 0; y_E = 14,96 см.

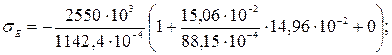
σ_E = – 2,23 ∙ 10⁷ ∙ (1 + 2,56) = – 79,388 ∙ 10⁶ = – 79,4 МПа.

Найдем напряжение растяжения в опасной точке D:

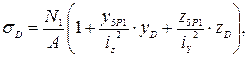
y_D и z_D – координаты точки D.

z_D = 0; y_D = – 19,04 см.

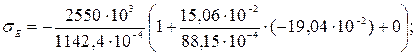
σ_D = – 2,23 ∙ 10⁷ ∙ (1 – 3,25) = 50,2 ∙ 10⁶ = 50,2 МПа.

Строим эпюру напряжений.

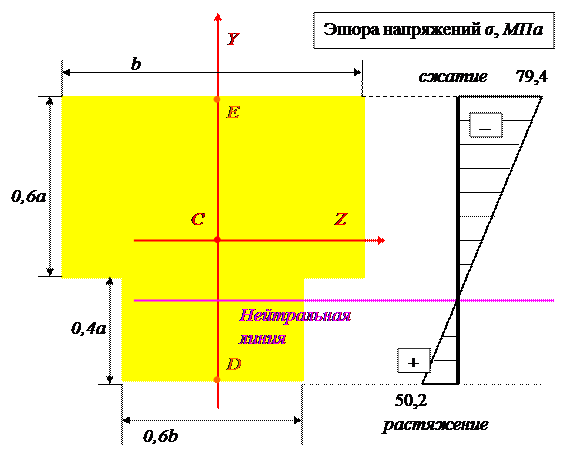
3) Построим эпюры нормальных напряжений в опасном сечении от продольной силы, изгибающего момента и их совместного действия (суммарную эпюру σ).