Темы курсовых работ по математическому анализу
1. Гиперболические функции.
2. Исследование функций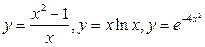 
и построение их графиков.
3. Исследование функций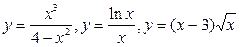 
и построение их графиков.
4. Исследование функций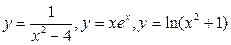 
и построение их графиков.
5. Исследование функций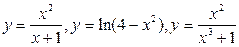 
и построение их графиков.
6. Исследование функций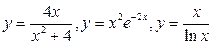 
и построение их графиков.
7. Исследование функций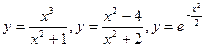 
и построение их графиков.
8. Исследование функций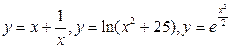 
и построение их графиков.
9. Исследование функций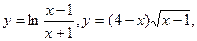 
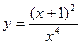и построение их графиков.
10. Исследование функций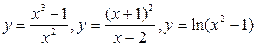 
и построение их графиков.
11. Исследование функций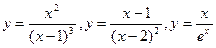 
и построение их графиков.
12. Исследование функций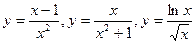 
и построение их графиков.
13. Исследование функций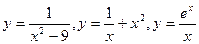 
и построение их графиков.
14. Исследование функций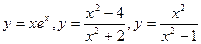 
и построение их графиков.
15. Эластичность функций одной и нескольких переменных.
16. Условный экстремум, метод множителей Лагранжа.
17. Частные производные и дифференциалы высших порядков.
18. Интегрирование рациональных дробей.
19. Интегрирование некоторых иррациональных выражений.
20. Двойной интеграл и его приложения.
21. Приближенные методы вычисления определенного интеграла.
22. Несобственные интегралы.
23. Разложение функций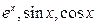 
в степенной ряд. Приближенные вычисления с помощью этих рядов.
24. Разложение функций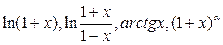 
в степенной ряд. Приближенные вычисления с помощью этих рядов.
25. Линейные дифференциальные уравнения с постоянными коэффициентами.
26. Приложения определенного интеграла.
27. Функции многих переменных, их дифференцирование.
28. Интегрирование тригонометрических функций.
29. Задача потребительского выбора.
30. Производственные функции.
Вопросы для подготовки к экзамену
1. Понятие функции. Сложная функция. График функции. Обратная функция. Элементарные функции.
2. Числовая последовательность. Предел числовой последовательности.
3. Свойства пределов.
4. Окрестность конечной и бесконечно удаленной точки. Предельная точка множества. Открытое и замкнутое множество, граничные точки. Проколотая окрестность конечной точки.
5. Бесконечно малые функции. Основные теоремы о бесконечно малых функциях. Бесконечно большие функции.
6. Определение предела функции в конечной и бесконечно удалённой точке. Первый и второй замечательный предел.
7. Свойства пределов функции.
8. Сравнение бесконечно малых функций. Эквивалентность бесконечно малых функций. Цепочка эквивалентных бесконечно малых функций.
9. Асимптоты к графику функции.
10. Непрерывность функции в точке. Арифметические операции над непрерывными функциями.
11. Основные теоремы о непрерывных функциях
12. Точки разрыва. Вертикальные асимптоты.
13. Понятие производной. Производные некоторых элементарных функций.
14. Таблица производных элементарных функций
15. Геометрический смысл производной. Уравнение касательной и нормали к графику функции.
16. Дифференциал. Свойства дифференциала
17. Понятие экстремума функции. Теоремы Ферма и Ролля.
18. Монотонность функции. Достаточное условие строгого возрастания (убывания функции). Достаточное условие экстремума функции.
19. Выпуклость графика функции. Точки перегиба. Достаточный признак выпуклости. Необходимый и достаточный признак точки перегиба.
20. Первообразная и неопределенный интеграл.
21. Свойства неопределенного интеграла.
22. Таблица интегралов.
23. Вычисление неопределенных интегралов методом подстановки.
24. Вычисление неопределенных интегралов интегрированием по частям.
25. Определенный интеграл.
26. Свойства определённого интеграла.
27. Формула Ньютона-Лейбница.
28. Вычисление определённых интегралов методом подстановки.
29. Вычисление определённых интегралов интегрированием по частям.
30. Вычисление площадей с помощью определённых интегралов.
31. Функции нескольких переменных.
32. Частные производные.
33. Полный дифференциал, его связь с частными производными.
34. Частные производные высших порядков.
35. Максимум функции нескольких переменных.
36. Минимум функции нескольких переменных.
37. Необходимое условие экстремума.
38. Достаточное условие экстремума.
39. Числовые ряды. Необходимый признак сходимости рядов.
40. Признак сравнения сходимости числовых рядов с положительными членами.
41. Признак сравнения сходимости числовых рядов с положительными членами в предельной форме.
42. Признак Коши сходимости числовых рядов с положительными членами.
43. Признак Даламбера сходимости числовых рядов с положительными членами.
44. Знакопеременные ряды. Абсолютная и условная сходимости рядов. Признак Лейбница.
45. Степенные ряды. Интервал сходимости степенного ряда.
46. Операции над степенными рядами.
47. Разложение в ряд Тейлора-Маклорена функций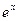 
, 
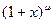
48. Разложение в ряд Тейлора-Маклорена функций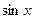 
, 
.
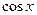49. Приближённые вычисления.
50. Дифференциальные уравнения первого порядка. Основные определения. Задача Коши.
51. Дифференциальные уравнения первого порядка: с разделяющимися переменными; однородные дифференциальные уравнения; линейные.
52. Линейные дифференциальные уравнения второго порядка, однородные и неоднородные. Понятие общего решения.
53. Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами. Теорема о структуре общего решения.
54. Неоднородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами . Теорема о структуре общего решения.
УЧЕБНО-МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по самостоятельной работе студентов
и проведению практических занятий
По дисциплине: «Математический анализ»
Направление подготовки: 080100.62 «Экономика»
Профиль подготовки: «Экономика предприятий и организаций (таможня)»
Квалификация выпускника: бакалавр
АВТОР
ЦвильМария Михайловна
Издано в авторской редакции
Подписано в печать 13. 09. 2012
Формат 64х84/16. Ксерокопия. Таймс. 1,4 усл. п. л.
Заказ № 3300 . Тираж 7 экз.
Российская таможенная академия Ростовский филиал
344002, г. Ростов-на-Дону, пр. Буденновский, 20