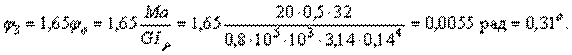Построение эпюры крутящих моментов

Найденное значение Х = 0,34кН×м подставляем в выражения (3.9), вы­числяя таким образом величину крутящего момента на каждом участке:

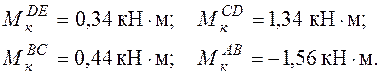
По найденным значениям 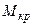строим эпюру крутящих моментов. Для это­го рассматриваем последовательно участки ЕD, DC, CB и CA. Крутящие мо­менты, действующие на этих участках, уже вычислены.

Величина крутящего момента на каждом участке не зависит от поло­же­ния се­че­ния в пределах участка (крутящий момент постоянен), поэтому эпю­ра кру­тя­щих моментов ограничена отрезками прямых (рис.7,б). Построенная эпюра позволяет найти опасное сечение, т.е. такое, в котором действует мак­си­маль­ный (по модулю) крутящий момент.

В рассматриваемом примере опасными будут сечения в пределах учас­т­ка АВ; расчетное значение крутящего момента

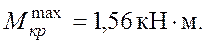
3. Подбор диаметра поперечного сечения бруса.

Используем условие прочности (3.4)

.

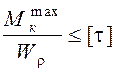Учитывая, что 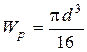, выразим диаметр из условия прочности

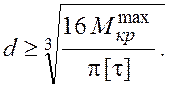
Подставляя 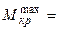1,56 кН×м и 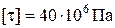, вычисляем диаметр по­пе­речного сечения, округляя его до стандартной величины:

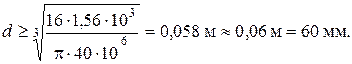
Проверка условия жесткости.

Условие жесткости записываем в форме (3.7):

.

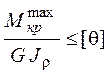По условию задачи [q]= 1 град/м. Переводя значение угла из градусной меры в радианную, получаем

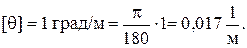
Вычисляем выражение, стоящее в левой части условия жесткости, опре­де­лив предварительно величину полярного момента инерции бруса:

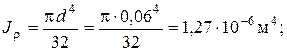
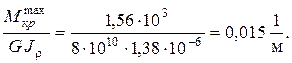
Сравнение левой и правой частей условия жесткости показывает, что оно вы­­по­л­­няется:

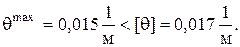
Построение эпюры углов закручивания.

Вычисляем углы закручивания по участкам, используя формулу (3.5):

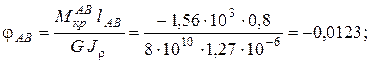
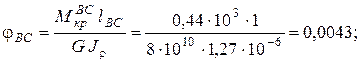
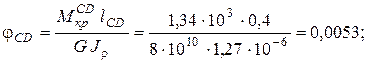
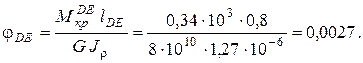
Угол поворота каждого сечения равен сумме углов закручивания соот­ветствующих участков бруса. Суммирование углов начинаем с незакрепленного кон­ца А:

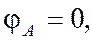так как сечение в заделке неподвижно;

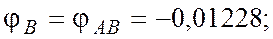
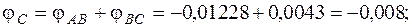
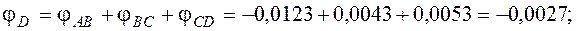
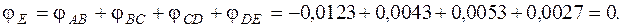
По вычисленным углам поворота сечений построена эпюра углов закру­чи­вания (рис. 7, в).

Равенство 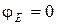является проверкой решения, так как неизвестный кру­тя­щий момент Х определялся из условия равенства нулю угла поворота сво­бод­ного конца бруса.

Вопросы для контроля знаний

1. При каком внутреннем силовом факторе возникает кручение?

2. Какие напряжения возникают в поперечных сечениях при кручении?

3. Как рассчитать максимальные напряжения при кручении?

4. Что такое полярный момент сопротивления и полярный момент инерции?

5.Напишите условие прочности при кручении.

6. Какая деформация возникает при кручении?

7. Как рассчитать угол закручивания круглого вала?

8. Как определяется допускаемое касательное напряжение ?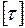

9. Как рассчитать необходимый диаметр вала при кручении, если 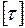и характернагружения вала известны?

Пример № 17 (Каримов)

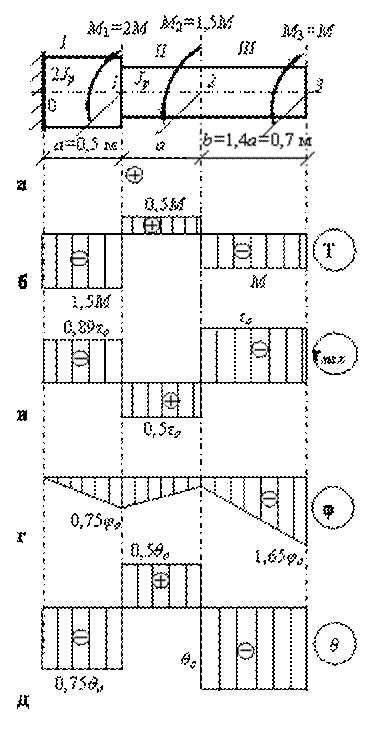
Прямолинейный круглый стальной стержень ступенчато-переменного диаметра жестко защемлен одним концом и нагружен системой трех внешних крутящих моментов (рис. 3.2.11, а), причем М₁ = 2М; М₂ = 1,5М; М₃ = М, а М = 20 кНм.

Построить эпюры крутящих моментовТ, абсолютных 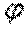и относительных 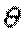углов закручивания стержня, эпюру наибольших касательных напряжений 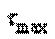в сечениях по всей длине стержня.

Из условий прочности и жесткости подобрать диаметры сплошного стержня для каждого участка, приняв в расчетах модуль сдвига G= 0,8·10⁵МПа, расчетное сопротивление материала стержня (сталь) на срез R_s= 100 МПа, допускаемый относительный угол закручивания 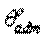= 0,4 град/м. Полярные моменты инерции и длины участков показаны на рис. а.

Решение.

Обозначим цифрами характерные сечения на стержне. Имеем для II и III участков

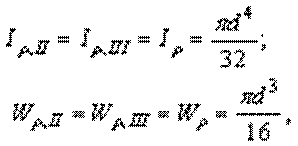(a)

где через d обозначен диаметр стержня в пределах этих участков. Для участка Iполучаем:

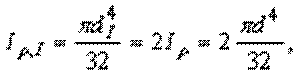
откуда находим 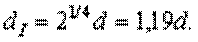(б)

Кроме того,

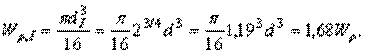(в)

Определим внутренние крутящие моменты на каждом участке, начиная со свободного конца:

T_III = –M₃ = –M; T_II = –M₃ + M₂ = –M + 1,5M = 0,5M;

T_I = –M₃ + M₂– M₁ = –M + 1,5M– 2M = –1,5M.

Строим эпюру крутящих моментовТ (рис. б).

Определяем наибольшие касательные напряжения на каждом участке, используя формулу

:

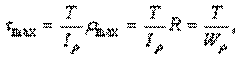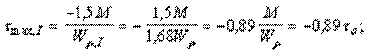
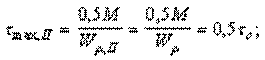
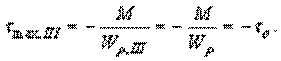
В последних формулах введено обозначение

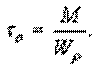(г)

Строим эпюру максимальных касательных напряжений по длине стержня (рис. в).

Определяем углы закручивания отдельных участков по формуле :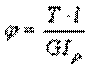

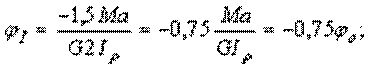
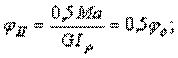
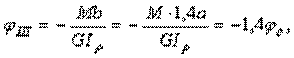
где введено новое обозначение

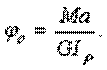(д)

Вычисляем углы поворота характерных сечений стержня:

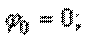
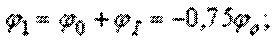
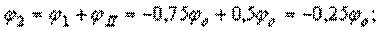
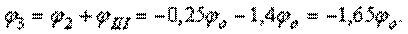
По полученным результатам строим эпюру 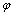(рис. г).

Определяем относительные углы закручивания на каждом участке стержня по формуле :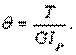

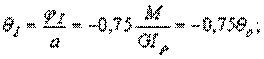
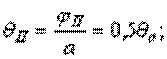
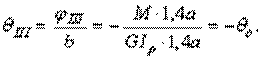
Строим эпюру 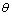(рис. д).

По эпюре 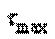(рис. в) видно, что самое большое касательное напряжение будет на участке III, поэтому формулу 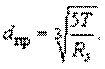записываем применительно к этому участку

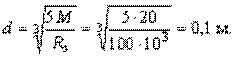
По эпюре 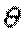очевидно, что самый большой относительный угол закручивания будет на участке III, поэтому применяем формулу 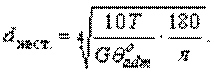для участка III:

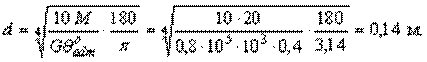
Сравнивая результаты расчетов на прочность (d= 0,1 м) и на жесткость (d= 0,14 м) находим, что главенствующим в рассматриваемой задаче является расчет на жесткость, поскольку d= 0,14 м > 0,1 м. Окончательно принимаем d= 14 см.

Определяем диаметры сечений остальных участков:

d_II = d_III = d =14 см,

d_I =1,19d = 16,7 см.

Определим значение угла закручивания 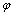на правом торце стержня (рис. а) в сечении 3. Из эпюры 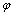(рис. г) выписываем с учетом формул (д) и (а):