Кинематическое исследование многозвенного плоского механизма.
Исходные данные: 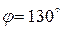 , а = 49 см, b = 19 см, с = 57 мм, О1А = 15 см,
, а = 49 см, b = 19 см, с = 57 мм, О1А = 15 см,
АВ = 40 см, О2В = 35 см, О2С = 30 см, ВС = 20 см, СD = 60 см, О3D = 50 см, СЕ = 30 см, ЕF=30 см. Кривошип О1А вращается с постоянной угловой скоростью ωО1=3с-1.
Для данного положения механизма определить скорости всех точек механизма, угловые скорости звеньев методами полюса и мгновенного центра скоростей (МЦС), а также ускорения точек А, В, М (точка М делит звено АВ пополам) методами полюса и мгновенного центра ускорений (МЦУ) и угловое ускорение звена АВ.
Решение.
1. Изобразим механизм в заданном положении, согласно геометрическим размерам приведенным в исходных данных, тогда схема механизма изобразится в соответствующем масштабе (рис.30).
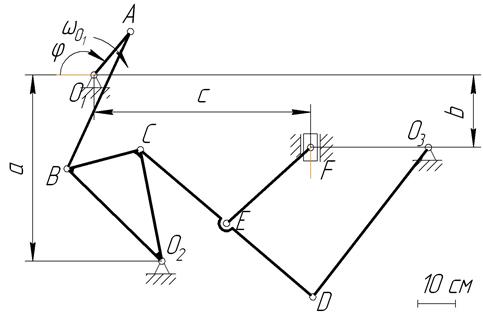
Рис.30.
2. Определим скорости точек механизма, и угловые скорости звеньев методом полюса с помощью построения плана скоростей.
2.1. Определим скорость точки А.
Точка А принадлежит звену АО1, которое совершает вращательное движение относительно неподвижной точки О1, тогда скорость точки будет равна
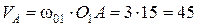 см/с.
см/с.
Вектор скорости точки А ( 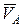 ) будет направлен перпендикулярно радиусу вращения АО1 в сторону вращения угловой скорости ωО1 (рис.31).
) будет направлен перпендикулярно радиусу вращения АО1 в сторону вращения угловой скорости ωО1 (рис.31).
Примем вектор Ра, который будет изображать вектор скорости точки А ( 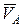 ) на плане скоростей, равным 120 мм (Ра = 120 мм).
) на плане скоростей, равным 120 мм (Ра = 120 мм).
Тогда масштаб плана скоростей составит
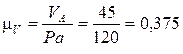 см/(с∙мм).
см/(с∙мм).
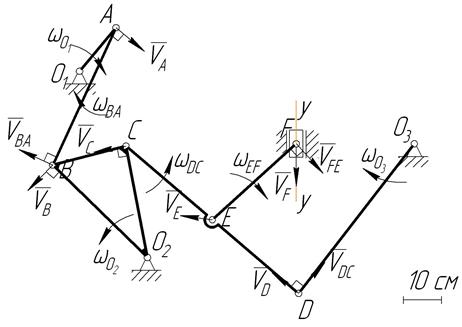
Рис.31.
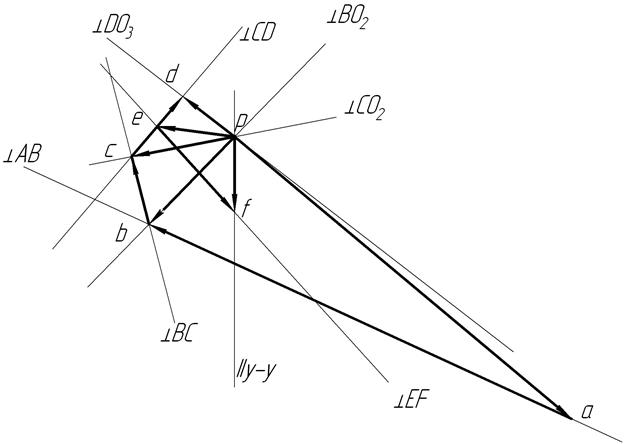
Рис.32. План скоростей, масштаб 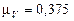 см/(с∙мм).
см/(с∙мм).
Изобразим вектор Ра, изображающего вектор скорости точки А ( 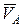 ), на плане скоростей равным 120 мм, путем параллельного переноса в точку Р вектора
), на плане скоростей равным 120 мм, путем параллельного переноса в точку Р вектора 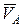 (рис.32).
(рис.32).
2.2. Определим скорость точки В.
Для нахождения скорости точки В требуется рассмотреть движение этой точки относительно двух полюсов, скорости которых известны.
Рассмотрим движение точки В относительно полюса точки А (так как скорость точки А определена). Составим векторное уравнение
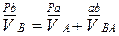 .
.
Согласно данному уравнению вектор скорости точки В ( 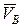 )изобразится вектором Pb на плане скоростей; вектор скорости точки А (
)изобразится вектором Pb на плане скоростей; вектор скорости точки А ( 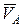 ) изображается вектором Pа на плане скоростей; вектор скорости
) изображается вектором Pа на плане скоростей; вектор скорости 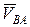 изобразится вектором аb на плане скоростей.
изобразится вектором аb на плане скоростей.
Под действием вектора скорости 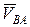 , приложенного в точке В, звено АВ будет приходить во вращение относительно уже неподвижного полюса точки А, с угловой скоростью
, приложенного в точке В, звено АВ будет приходить во вращение относительно уже неподвижного полюса точки А, с угловой скоростью 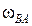 . Так как вектор скорости
. Так как вектор скорости 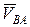 направлен перпендикулярно звену АВ (
направлен перпендикулярно звену АВ ( 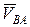 ÖАВ), то данную линию проводим из точки а на плане скоростей (см. рис.32).
ÖАВ), то данную линию проводим из точки а на плане скоростей (см. рис.32).
Составим второе векторное уравнение за полюс возьмем точку О2, так как относительно этой точки звено ВСО2 вращается (рис.31), то точка О2 является неподвижной, поскольку закреплена в шарнирно неподвижной опоре, скорость точки О2 (  ) равна нулю.
) равна нулю.
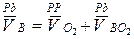 .
.
Так как 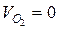 , следовательно, вектор, изображающий на плане скоростей
, следовательно, вектор, изображающий на плане скоростей 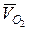 , будет находиться в точке Р (РР=0).
, будет находиться в точке Р (РР=0).
Под действием вектора скорости 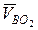 , приложенного в точке В, звено ВСО2 будет приходить во вращение относительно неподвижного полюса точки О2, с угловой скоростью
, приложенного в точке В, звено ВСО2 будет приходить во вращение относительно неподвижного полюса точки О2, с угловой скоростью 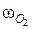 . Так как вектор скорости
. Так как вектор скорости 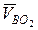 направлен перпендикулярно звену ВО2 (
направлен перпендикулярно звену ВО2 ( 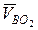 ÖВО2), то данную линию проводим из точки Р на плане скоростей (рис.32).
ÖВО2), то данную линию проводим из точки Р на плане скоростей (рис.32).
В пересечении двух линий (ÖВО2) и (ÖАВ) на плане скоростей определяем точку b.
Для нахождения скорости точки В по модулю ( 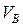 ) необходимо замерить отрезок Pb на плане скоростей и умножить на масштаб плана скоростей
) необходимо замерить отрезок Pb на плане скоростей и умножить на масштаб плана скоростей 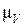 (Pb составит 33,3 мм)
(Pb составит 33,3 мм)
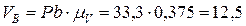 см/с.
см/с.
Для изображения вектора скорости точки В ( 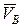 ) на схеме механизма требуется вектор Pb с плана скоростей (см. рис.32) параллельно перенести в точку В механизма (см. рис.31).
) на схеме механизма требуется вектор Pb с плана скоростей (см. рис.32) параллельно перенести в точку В механизма (см. рис.31).
2.3. Определим угловую скорость звена АВ ( 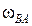 ).
).
Звено АВ приобретает угловую скорость 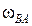 , относительно неподвижной точки А под действием скорости точки В, относительно точки А (
, относительно неподвижной точки А под действием скорости точки В, относительно точки А ( 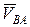 ). Для определения модуля скорости
). Для определения модуля скорости 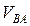 необходимо на плане скоростей (см. рис.32) измерить отрезок ab и умножить на масштаб плана скоростей
необходимо на плане скоростей (см. рис.32) измерить отрезок ab и умножить на масштаб плана скоростей 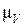 (аb составит 126,9 мм).
(аb составит 126,9 мм).
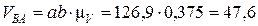 см/с.
см/с.
Для изображения вектора скорости 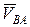 из точки В на схеме механизма требуется вектор аb с плана скоростей (см. рис.32) параллельно перенести в точку В механизма (см. рис.31).
из точки В на схеме механизма требуется вектор аb с плана скоростей (см. рис.32) параллельно перенести в точку В механизма (см. рис.31).
Тогда угловая скорость 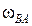 звена АВ относительно центра вращения точки А, под действием вектора скорости
звена АВ относительно центра вращения точки А, под действием вектора скорости 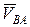 направлена по часовой стрелке на схеме механизма (рис.31). Определим численное значение угловой скорости
направлена по часовой стрелке на схеме механизма (рис.31). Определим численное значение угловой скорости 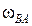
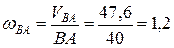 с-1.
с-1.
2.4. Определим угловую скорость звена ВСО2 ( 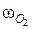 ).
).
Звено ВСО2 приобретает угловую скорость 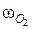 относительно неподвижной точки О2, под действием скорости точки В, относительно точки О2 (
относительно неподвижной точки О2, под действием скорости точки В, относительно точки О2 ( 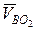 ). Вектор скорости
). Вектор скорости 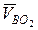 равен вектору
равен вектору 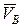 , см. п.2.2.
, см. п.2.2.
Тогда угловая скорость 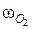 звена ВСО2 относительно центра вращения точки О2 под действием вектора скорости
звена ВСО2 относительно центра вращения точки О2 под действием вектора скорости 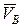 направлена против часовой стрелки на схеме механизма (см. рис.31). Определим численное значение угловой скорости
направлена против часовой стрелки на схеме механизма (см. рис.31). Определим численное значение угловой скорости 
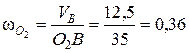 с-1.
с-1.
2.5. Определим скорость точки С.
Для нахождения скорости точки С, рассмотрим движение этой точки относительно двух полюсов (точки В, О2), скорости которых известны.
Рассмотрим движение точки С относительно полюса точки В. Составим векторное уравнение
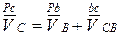 .
.
Согласно данному уравнению вектор скорости точки С ( 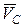 )изобразится вектором Pс на плане скоростей; вектор скорости точки В (
)изобразится вектором Pс на плане скоростей; вектор скорости точки В ( 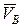 ) изобразится вектором Pb на плане скоростей; вектор скорости
) изобразится вектором Pb на плане скоростей; вектор скорости 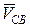 изобразится вектором bс на плане скоростей.
изобразится вектором bс на плане скоростей.
Под действием вектора скорости 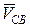 , приложенного в точке С, звено ВС будет приходить во вращение относительно уже неподвижного полюса точки В. Так как вектор скорости
, приложенного в точке С, звено ВС будет приходить во вращение относительно уже неподвижного полюса точки В. Так как вектор скорости 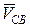 направлен перпендикулярно звену ВС (
направлен перпендикулярно звену ВС ( 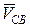 ÖСВ), то данную линию проводим из точки b на плане скоростей (см. рис.32).
ÖСВ), то данную линию проводим из точки b на плане скоростей (см. рис.32).
Составим второе векторное уравнение за полюс возьмем точку О2.
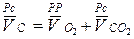 .
.
где 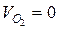 , вектор изображающий на плане скоростей
, вектор изображающий на плане скоростей 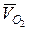 будет находиться в точке Р (РР = 0).
будет находиться в точке Р (РР = 0).
Так как вектор скорости 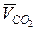 направлен перпендикулярно звену СО2 (
направлен перпендикулярно звену СО2 ( 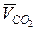 ÖСО2), то данную линию проводим из точки Р на плане скоростей (см. рис.32).
ÖСО2), то данную линию проводим из точки Р на плане скоростей (см. рис.32).
В пересечении двух линий (ÖСО2) и (ÖВС) на плане скоростей определяем точку с.
Для нахождения скорости точки С по модулю ( 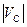 ), необходимо замерить отрезок Pс на плане скоростей и умножить на масштаб плана скоростей
), необходимо замерить отрезок Pс на плане скоростей и умножить на масштаб плана скоростей 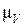 (Pс составит 28,5 мм).
(Pс составит 28,5 мм).
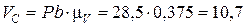 см/с.
см/с.
Для изображения вектора скорости точки С ( 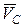 ) на схеме механизма требуется вектор Pс с плана скоростей (см. рис.32) параллельно перенести в точку С механизма (см. рис.31).
) на схеме механизма требуется вектор Pс с плана скоростей (см. рис.32) параллельно перенести в точку С механизма (см. рис.31).
Угловая скорость звена ВСО2 определена 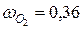 с-1
с-1
2.6. Определим скорость точки D.
Для нахождения скорости точки D, требуется рассмотреть движение этой точки относительно двух полюсов, скорости которых известны.
Рассмотрим движение точки D относительно полюса точки C (так как скорость точки C определена). Составим векторное уравнение
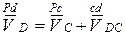 .
.
Согласно данному уравнению вектор скорости точки D ( 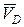 )изобразится вектором Pd на плане скоростей; вектор скорости точки C (
)изобразится вектором Pd на плане скоростей; вектор скорости точки C ( 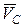 ) изобразится вектором Pc на плане скоростей; вектор скорости
) изобразится вектором Pc на плане скоростей; вектор скорости 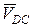 изобразится вектором сd на плане скоростей.
изобразится вектором сd на плане скоростей.
Под действием вектора скорости 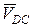 , приложенного в точке D, звено CD будет приходить во вращение относительно уже неподвижного полюса точки С, с угловой скоростью
, приложенного в точке D, звено CD будет приходить во вращение относительно уже неподвижного полюса точки С, с угловой скоростью 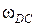 . Так как вектор скорости
. Так как вектор скорости 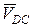 направлен перпендикулярно звену CD (
направлен перпендикулярно звену CD ( 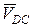 ÖCD), то данную линию проводим из точки с на плане скоростей (см. рис.32).
ÖCD), то данную линию проводим из точки с на плане скоростей (см. рис.32).
Составим второе векторное уравнение, за полюс возьмем точку О3, так как относительно этой точки звено DО3 вращается (рис.31), то точка О3 является неподвижной, поскольку закреплена в шарнирно неподвижной опоре, скорость точки О3 ( 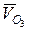 ) равна нулю.
) равна нулю.
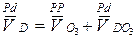 .
.
Так как 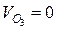 , следовательно, вектор изображающий на плане скоростей
, следовательно, вектор изображающий на плане скоростей 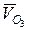 , будет находиться в точке Р (РР = 0).
, будет находиться в точке Р (РР = 0).
Под действием вектора скорости 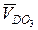 , приложенного в точке D, звено DО3 будет приходить во вращение относительно неподвижного полюса точки О3, с угловой скоростью
, приложенного в точке D, звено DО3 будет приходить во вращение относительно неподвижного полюса точки О3, с угловой скоростью  . Так как вектор скорости
. Так как вектор скорости 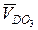 направлен перпендикулярно звену DО3 (
направлен перпендикулярно звену DО3 ( 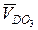 ÖDО3), то данную линию проводим из точки Р на плане скоростей (рис.32).
ÖDО3), то данную линию проводим из точки Р на плане скоростей (рис.32).
В пересечении двух линий (ÖDО3) и (ÖCD) на плане скоростей определяем точку d.
Для нахождения скорости точки D по модулю ( 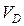 ), необходимо замерить отрезок Pd на плане скоростей и умножить на масштаб плана скоростей
), необходимо замерить отрезок Pd на плане скоростей и умножить на масштаб плана скоростей 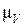 (Pd составит 18 мм).
(Pd составит 18 мм).
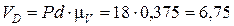 см/с.
см/с.
Для изображения вектора скорости точки D ( 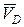 ) на схеме механизма, требуется вектор Pd с плана скоростей (см. рис.32) параллельно перенести в точку D механизма (см. рис.31).
) на схеме механизма, требуется вектор Pd с плана скоростей (см. рис.32) параллельно перенести в точку D механизма (см. рис.31).
2.7. Определим угловую скорость звена DC ( 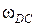 ).
).
Звено DC приобретает угловую скорость 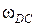 , относительно неподвижной точки C; под действием скорости точки D – относительно точки C (
, относительно неподвижной точки C; под действием скорости точки D – относительно точки C ( 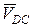 ). Для определения модуля скорости
). Для определения модуля скорости 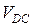 необходимо на плане скоростей (см. рис.32) измерить отрезок cd и умножить на масштаб плана скоростей
необходимо на плане скоростей (см. рис.32) измерить отрезок cd и умножить на масштаб плана скоростей 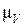 (cd составит 21,6 мм).
(cd составит 21,6 мм).
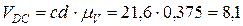 см/с
см/с
Для изображения вектора скорости 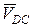 из точки D на схеме механизма требуется вектор cd с плана скоростей (см. рис.32) параллельно перенести в точку D механизма (см. рис.31).
из точки D на схеме механизма требуется вектор cd с плана скоростей (см. рис.32) параллельно перенести в точку D механизма (см. рис.31).
Тогда угловая скорость 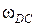 звена DC относительно центра вращения точки C, под действием вектора скорости
звена DC относительно центра вращения точки C, под действием вектора скорости 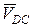 направлена против часовой стрелки на схеме механизма (см. рис.31). Определим численное значение угловой скорости
направлена против часовой стрелки на схеме механизма (см. рис.31). Определим численное значение угловой скорости 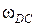
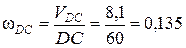 с-1.
с-1.
2.8. Определим угловую скорость звена DО3 ( 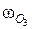 ).
).
Звено DО3 приобретает угловую скорость 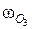 относительно неподвижной точки О3; под действием скорости точки D – относительно точки О3 (
относительно неподвижной точки О3; под действием скорости точки D – относительно точки О3 ( 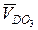 ). Вектор скорости
). Вектор скорости 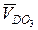 равен вектору
равен вектору 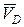 , см. п.2.6.
, см. п.2.6.
Тогда угловая скорость 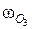 звена DО3 относительно центра вращения точки О3, под действием вектора скорости
звена DО3 относительно центра вращения точки О3, под действием вектора скорости  направлена по часовой стрелки на схеме механизма (рис.31). Определим численное значение угловой скорости
направлена по часовой стрелки на схеме механизма (рис.31). Определим численное значение угловой скорости 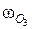
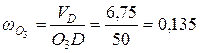 с-1.
с-1.
2.9. Определим скорость точки E.
Так как точка Е принадлежит звену СD, у которого определены кинематические характеристики (скорости точек С, D), то положение точки е в плане скоростей определим методом обхода точек. Составим соотношение
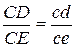
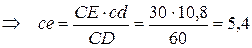 мм.
мм.
Изобразим отрезок ce на плане скоростей (см. рис.31) из точки с в направлении точки d. Тогда вектор скорости точки Е ( 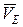 ) изобразится на плане скоростей вектором Ре, численное значение скорости
) изобразится на плане скоростей вектором Ре, численное значение скорости 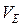 составит
составит
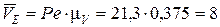 см/с.
см/с.
Для изображения вектора скорости точки Е ( 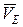 ) на схеме механизма, требуется вектор Pе с плана скоростей (см. рис.32) параллельно перенести в точку Е механизма (см. рис.31).
) на схеме механизма, требуется вектор Pе с плана скоростей (см. рис.32) параллельно перенести в точку Е механизма (см. рис.31).
2.10. Определим скорость точки F.
Для нахождения скорости точки F, требуется рассмотреть движение этой точки относительно двух полюсов, скорости которых известны.
Рассмотрим движение точки F относительно полюса точки E (так как скорость точки E определена). Составим векторное уравнение
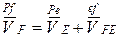 .
.
Согласно данному уравнению вектор скорости точки F ( 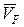 )изобразится вектором Pf на плане скоростей; вектор скорости точки E (
)изобразится вектором Pf на плане скоростей; вектор скорости точки E ( 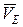 ) изобразится вектором Pe на плане скоростей; вектор скорости
) изобразится вектором Pe на плане скоростей; вектор скорости 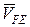 изобразится вектором ef на плане скоростей.
изобразится вектором ef на плане скоростей.
Под действием вектора скорости 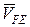 приложенного в точке F звено FE будет приходить во вращение относительно уже неподвижного полюса точки E с угловой скоростью
приложенного в точке F звено FE будет приходить во вращение относительно уже неподвижного полюса точки E с угловой скоростью 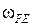 . Так как вектор скорости
. Так как вектор скорости 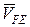 направлен перпендикулярно звену FE (
направлен перпендикулярно звену FE ( 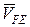 ÖFE), то данную линию проводим из точки e на плане скоростей (см. рис.32).
ÖFE), то данную линию проводим из точки e на плане скоростей (см. рис.32).
Составим второе векторное уравнение, за полюс возьмем ось у - у, так как относительно этой оси точка F движется прямолинейно вдоль оси у - у (совершает возвратно-поступательное движение). Поскольку система отсчета ось у-у неподвижна (см. рис.31), то скорость оси у-у ( 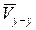 ) равна нулю
) равна нулю
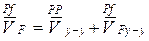 .
.
Так как 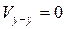 , следовательно, вектор изображающий на плане скоростей
, следовательно, вектор изображающий на плане скоростей 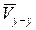 , будет находиться в точке Р (РР=0).
, будет находиться в точке Р (РР=0).
Вектор скорости 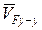 направлен вдоль оси у-у (
направлен вдоль оси у-у ( 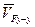 //у-у), данную линию проводим из точки Р на плане скоростей (см. рис.32).
//у-у), данную линию проводим из точки Р на плане скоростей (см. рис.32).
В пересечении двух линий (ÖFE) и (//у-у) на плане скоростей определяем точку f.
Для нахождения скорости точки F по модулю ( 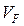 ), необходимо замерить отрезок Pf на плане скоростей и умножить на масштаб плана скоростей
), необходимо замерить отрезок Pf на плане скоростей и умножить на масштаб плана скоростей 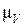 (Pf составит 20,6 мм).
(Pf составит 20,6 мм).
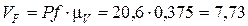 см/с.
см/с.
Для изображения вектора скорости точки F ( 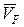 ) на схеме механизма, требуется вектор Pf с плана скоростей (рис.32) параллельно перенести в точку F механизма (рис.31).
) на схеме механизма, требуется вектор Pf с плана скоростей (рис.32) параллельно перенести в точку F механизма (рис.31).
2.11. Определим угловую скорость звена FE ( 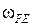 ).
).
Поскольку звено FE приобретает угловую скорость 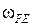 относительно неподвижной точки Е; под действием скорости точки F – относительно точки E (
относительно неподвижной точки Е; под действием скорости точки F – относительно точки E ( 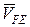 ), для определения модуля скорости
), для определения модуля скорости 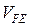 необходимо на плане скоростей (рис.32) измерить отрезок ef и умножить на масштаб плана скоростей
необходимо на плане скоростей (рис.32) измерить отрезок ef и умножить на масштаб плана скоростей 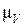 (ef составит 31,7мм).
(ef составит 31,7мм).
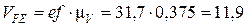 см/с.
см/с.
Для изображения вектора скорости 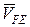 из точки F на схеме механизма, требуется вектор ef с плана скоростей (см. рис.32) параллельно перенести в точку F механизма (см. рис.31).
из точки F на схеме механизма, требуется вектор ef с плана скоростей (см. рис.32) параллельно перенести в точку F механизма (см. рис.31).
Тогда угловая скорость 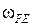 звена FE относительно центра вращения точки E, под действием вектора скорости
звена FE относительно центра вращения точки E, под действием вектора скорости 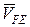 направлена по часовой стрелке на схеме механизма (рис.31). Определим численное значение угловой скорости
направлена по часовой стрелке на схеме механизма (рис.31). Определим численное значение угловой скорости 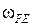
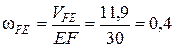 с-1.
с-1.
3. Определим скорости точек механизма, и угловые скорости звеньев методом мгновенного центра скоростей (МЦС).
Исходная схема изображена на рис.30.
3.1.Определим скорость точки А.
Точка А принадлежит звену АО1, которое совершает вращательное движение относительно неподвижной точки О1, тогда МЦС звена АО1 находится в точке О1.
Скорость точки будет равна
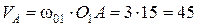 см/с.
см/с.
Вектор скорости точки А ( 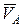 ) будет направлен перпендикулярно радиусу вращения АО1 в сторону вращения угловой скорости ωО1 (рис.33).
) будет направлен перпендикулярно радиусу вращения АО1 в сторону вращения угловой скорости ωО1 (рис.33).
3.2. Определим скорость точки В и угловую скорость звена АВ.
Для нахождения скорости точки В, требуется определить положение МЦС звена АВ точки РАВ. МЦС звена АВ находится в пересечении перпендикуляров к векторам скоростей точек А и В. Из точки А к вектору 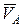 проводим перпендикуляр (рис.33); точка В вращается относительно неподвижной точки О2, тогда вектор скорости
проводим перпендикуляр (рис.33); точка В вращается относительно неподвижной точки О2, тогда вектор скорости 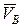 направлен из точки В перпендикулярно радиусу вращения ВО2, следовательно, перпендикуляр к скорости
направлен из точки В перпендикулярно радиусу вращения ВО2, следовательно, перпендикуляр к скорости 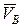 проходит вдоль звена ВО2 (см. рис.33). В пересечении этих двух линий находится МЦС звена АВ, точка РАВ. Относительно точки РАВ звено АВ, под действием вектора скорости
проходит вдоль звена ВО2 (см. рис.33). В пересечении этих двух линий находится МЦС звена АВ, точка РАВ. Относительно точки РАВ звено АВ, под действием вектора скорости 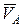 , вращается с угловой скоростью
, вращается с угловой скоростью 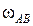 по часовой стрелке. Численное значение угловой скорости звена АВ составит
по часовой стрелке. Численное значение угловой скорости звена АВ составит
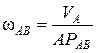 .
.
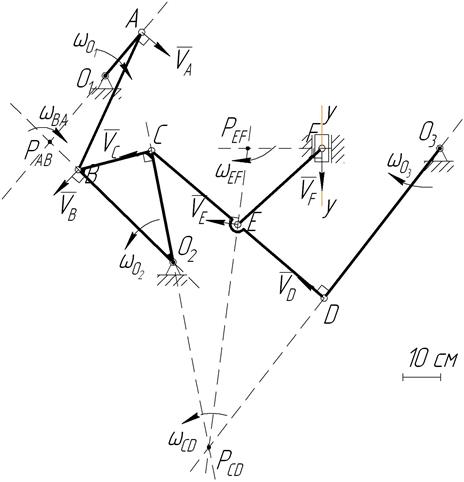
Рис.33.
где АРАВ – радиус вращения точки А, относительно МЦС звена АВ (рис.33).
Данный отрезок требуется замерить и привести к размерностям исходных данных (АРАВ составит 37,8 см)
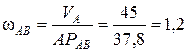 с-1.
с-1.
Поскольку точка В вращается на звене АВ относительно МЦС, то скорость точки В составит (BРАВ равен 10,3 см)
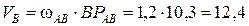 см/с.
см/с.
Вектор скорости точки В (  ) направлен из точки В перпендикулярно радиусу вращения ВРАВ в сторону вращения угловой скорости
) направлен из точки В перпендикулярно радиусу вращения ВРАВ в сторону вращения угловой скорости  (см. рис.33).
(см. рис.33).
3.3.Определим угловую скорость звена ВСО2 ( 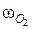 ).
).
Поскольку звено ВСО2 совершает вращательное движение относительно неподвижной точки О2, то в точке О2 располагается МЦС звена ВСО2. Под действием скорости точки В ( 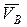 ) относительно точки О2, звено ВСО2 приобретает угловую скорость
) относительно точки О2, звено ВСО2 приобретает угловую скорость 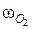 , направленную против часовой стрелки (рис.33).
, направленную против часовой стрелки (рис.33).
Определим численное значение угловой скорости 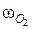
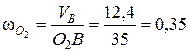 с-1.
с-1.
3.4.Определим скорость точки С.
Так как точка С принадлежит звену ВСО2, которое вращается относительно МЦС точки О2, вектор скорости точки С ( 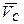 ) направлен перпендикулярно радиусу вращения СО2 в сторону угловой скорости
) направлен перпендикулярно радиусу вращения СО2 в сторону угловой скорости 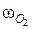 (см. рис.33). Численное значение скорости точки С составит
(см. рис.33). Численное значение скорости точки С составит
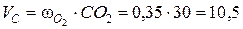 см/с.
см/с.
3.5. Определим скорость точки D и угловую скорость звена CD.
Для нахождения скорости точки D требуется определить положение МЦС звена CD точки РCD. МЦС звена CD находится в пересечении перпендикуляров к векторам скоростей точек C и D. Из точки C к вектору 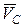 проводим перпендикуляр (см. рис.33); точка D вращается относительно неподвижной точки О3, тогда вектор скорости
проводим перпендикуляр (см. рис.33); точка D вращается относительно неподвижной точки О3, тогда вектор скорости 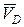 направлен из точки D перпендикулярно радиусу вращения DО3, следовательно, перпендикуляр к скорости
направлен из точки D перпендикулярно радиусу вращения DО3, следовательно, перпендикуляр к скорости 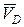 проходит вдоль звена DО3 (см. рис.33). На пересечении этих двух линий находится МЦС звена CD, точка РCD. Относительно точки РCD звено CD под действием вектора скорости
проходит вдоль звена DО3 (см. рис.33). На пересечении этих двух линий находится МЦС звена CD, точка РCD. Относительно точки РCD звено CD под действием вектора скорости 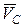 вращается с угловой скоростью
вращается с угловой скоростью 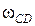 против часовой стрелки. Численное значение угловой скорости звена CD составит
против часовой стрелки. Численное значение угловой скорости звена CD составит
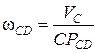 ,
,
где СРСD – радиус вращения точки C, относительно МЦС звена CD (см. рис.33).
Данный отрезок требуется замерить и привести к размерностям исходных данных (СРСD составит 79,8 см)
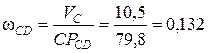 с-1.
с-1.
Поскольку точка D вращается на звене CD относительно МЦС, то скорость точки D составит
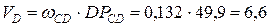 см/с,
см/с,
где DРCD равен 49,9 см.
Вектор скорости точки D ( 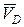 ) направлен из точки D перпендикулярно радиусу вращения DРСD в сторону вращения угловой скорости
) направлен из точки D перпендикулярно радиусу вращения DРСD в сторону вращения угловой скорости 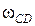 (см. рис.33).
(см. рис.33).
3.6.Определим угловую скорость звена DО3 ( 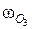 ).
).
Поскольку звено DО3 совершает вращательное движение относительно неподвижной точки О3, то точка О3 является МЦС звена DО3. Под действием скорости точки D ( 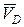 ) звено DО3 приобретает угловую скорость
) звено DО3 приобретает угловую скорость 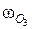 относительно МЦС точки О3 в направлении движения часовой стрелки. Определим численное значение угловой скорости
относительно МЦС точки О3 в направлении движения часовой стрелки. Определим численное значение угловой скорости 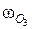
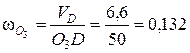 с-1.
с-1.
3.7.Определим скорость точки Е.
Так как точка Е принадлежит звену CD, которое вращается относительно МЦС точки РСD, то вектор скорости точки Е ( 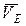 ) направлен перпендикулярно радиусу вращения ЕРСD в сторону угловой скорости
) направлен перпендикулярно радиусу вращения ЕРСD в сторону угловой скорости 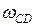 (см. рис.33). Численное значение скорости точки Е составит (EРCD равен 60 см)
(см. рис.33). Численное значение скорости точки Е составит (EРCD равен 60 см)
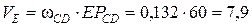 см/с.
см/с.
3.8. Определим скорость точки F и угловую скорость звена EF.
Для нахождения скорости точки F требуется определить положение МЦС звена EF точки РEF. МЦС звена EF находится на пересечении перпендикуляров к векторам скоростей точек Е и F. Из точки E к вектору 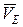 проводим перпендикуляр (см. рис.33); точка F движется прямолинейно вдоль оси у-у (совершает возвратно-поступательное движение). Вектор скорости
проводим перпендикуляр (см. рис.33); точка F движется прямолинейно вдоль оси у-у (совершает возвратно-поступательное движение). Вектор скорости 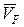 направлен вдоль оси у-у (
направлен вдоль оси у-у ( 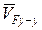 //у-у), восстанавливаем перпендикуляр к оси у-у из точки F.
//у-у), восстанавливаем перпендикуляр к оси у-у из точки F.
В пересечении этих двух линий находится МЦС звена EF – точка РEF. Относительно точки РEF звено EF, под действием вектора скорости 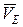 , вращается с угловой скоростью
, вращается с угловой скоростью 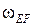 по часовой стрелке. Численное значение угловой скорости звена EF составит
по часовой стрелке. Численное значение угловой скорости звена EF составит
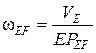 ,
,
где ЕРЕF – радиус вращения точки E относительно МЦС звена EF (рис.33), данный отрезок требуется замерить и привести к размерностям исходных данных (ЕРЕF составит 20,3см)
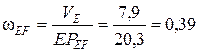 с-1.
с-1.
Поскольку точка F вращается на звене EF относительно МЦС, то скорость точки F составит (FРEF равен 19,6см)
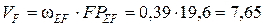 см/с.
см/с.
Вектор скорости точки F (  ) направлен из точки F перпендикулярно радиусу вращения FРEF в сторону вращения угловой скорости
) направлен из точки F перпендикулярно радиусу вращения FРEF в сторону вращения угловой скорости  (см. рис.33).
(см. рис.33).
4. Проверка допустимости приведенных расчетов скоростей многозвенного механизма методами плана и МЦС.
Таблица 3.
| Сравниваемая величина | По методу плана | По методу МЦС | Процент расхождения, 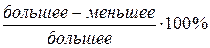 |
| VA | 0% | ||
| VB | 12,5 | 12,4 | 0,8% |
| VC | 10,7 | 10,5 | 1,9% |
| VD | 6,75 | 6,6 | 2,2% |
| VE | 7,9 | 1,3% | |
| VF | 7,73 | 7,65 | 1% |
| ωAB | 1,2 | 1,2 | 0% |
| ωCD | 0,135 | 0,132 | 2,2% |
| ωEF | 0,4 | 0,39 | 2,5% |
| ωO2 | 0,36 | 0,35 | 2,8% |
| ωO3 | 0,135 | 0,132 | 2,2% |
Если расхождение сравниваемых величин не превышает 5%, то приведенное решение считается верным.
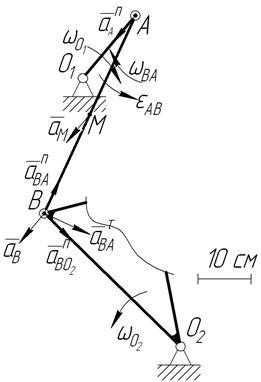
5. Определим ускорения точек А, В, М.
5.1. Методом полюса с помощью построения плана ускорений.
5.1.1. Определим ускорение точки А (  ).
).
Точка А вращается относительно неподвижной точки О1 с постоянной угловой скоростью ωО1 = 3с-1.
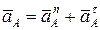 , (81)
, (81)
где 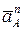 – нормальное (центростремительное) ускорение точки А на звене АО1;
– нормальное (центростремительное) ускорение точки А на звене АО1;
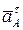 – касательное ускорение точки А на звене АО1.
– касательное ускорение точки А на звене АО1.
Нормальное ускорение составит
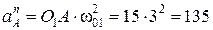 см /с2.
см /с2.
 Вектор
Вектор 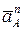 направлен из точки А к центру вращения точке О1 на схеме механизма (рис.34).
направлен из точки А к центру вращения точке О1 на схеме механизма (рис.34).
Касательное ускорение составит
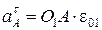 .
.
Так как угловая скорость вращения постоянна, то 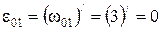 , то
, то 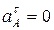 .
.
Тогда, согласно уравнению (81)
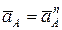 .
.
Изобразим вектор ускорения точки А на плане ускорений (рис. 35). Пусть вектор  изображается на плане ускорений вектором
изображается на плане ускорений вектором 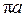 ; примем
; примем 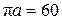 мм. Масштаб плана ускорений составит
мм. Масштаб плана ускорений составит
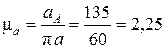 см/(мм∙с2).
см/(мм∙с2).
|
 ) и угловое ускорение звена АВ (
) и угловое ускорение звена АВ ( 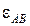 ).
). Рассмотрим движение точки В относительно полюса точки А, составим первое векторное уравнение
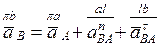 ,
,
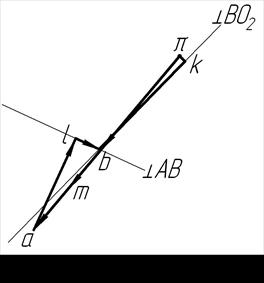
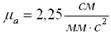 где
где  – нормальное ускорение точки В во вращательном движении относительно неподвижного полюса точки А; на плане ускорений вектор
– нормальное ускорение точки В во вращательном движении относительно неподвижного полюса точки А; на плане ускорений вектор  изобразится вектором al;
изобразится вектором al;
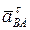 – касательное (вращательное) ускорение точки В во вращательном движении относительно неподвижного полюса точки А; на плане ускорений вектор
– касательное (вращательное) ускорение точки В во вращательном движении относительно неподвижного полюса точки А; на плане ускорений вектор 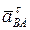 изобразится вектором lb;
изобразится вектором lb;
|
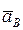 – вектор ускорения точки В; на плане ускорений вектор
– вектор ускорения точки В; на плане ускорений вектор 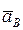 изобразится вектором
изобразится вектором 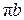 .
. Численное значение нормального ускорения составит
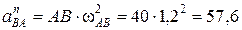 см /с2.
см /с2.
Вектор нормального ускорения точки В относительно полюса точки А ( 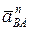 ) направлен из точки В к точке А на схеме механизма (рис. 34). На плане ускорений (рис. 35) вектор
) направлен из точки В к точке А на схеме механизма (рис. 34). На плане ускорений (рис. 35) вектор 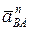 изобразится из точки а, длина al составит
изобразится из точки а, длина al составит
al= 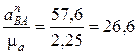 мм.
мм.
Вектор ускорения 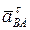 направлен из точки В перпендикулярно звену АВ на схеме механизма (
направлен из точки В перпендикулярно звену АВ на схеме механизма ( 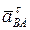 ÖВА) (см. рис. 34). На плане ускорений (см. рис. 35) из точки l изображаем линию, вдоль которой направлен вектор ускорения
ÖВА) (см. рис. 34). На плане ускорений (см. рис. 35) из точки l изображаем линию, вдоль которой направлен вектор ускорения 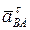 .
.
Рассмотрим движение точки В относительно полюса точки О2, составим второе векторное уравнение ускорений
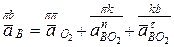 ,
,
где 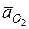 – ускорение точки О2; точка О2 является неподвижной, поскольку закреплена в шарнирнонеподвижной опоре, ускорение точки О2 (
– ускорение точки О2; точка О2 является неподвижной, поскольку закреплена в шарнирнонеподвижной опоре, ускорение точки О2 ( 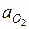 ) равна нулю, следовательно, изобразится на плане ускорений
) равна нулю, следовательно, изобразится на плане ускорений
вектором 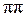 (
( 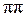 = 0).
= 0).
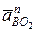 – нормальное ускорение точки В во вращательном движении относительно неподвижного полюса точки О2; на плане ускорений вектор
– нормальное ускорение точки В во вращательном движении относительно неподвижного полюса точки О2; на плане ускорений вектор 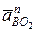 изобразится вектором
изобразится вектором 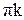 ;
;
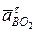 – касательное (вращательное) ускорение точки В во вращательном движении относительно неподвижного полюса точки О2; на плане ускорений вектор
– касательное (вращательное) ускорение точки В во вращательном движении относительно неподвижного полюса точки О2; на плане ускорений вектор 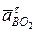 изобразится вектором
изобразится вектором 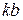 .
.
Численное значение нормального ускорения составит
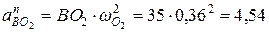 см /с2.
см /с2.
Вектор нормального ускорения точки В относительно полюса точки О2 ( 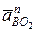 ) направлен из точки В к точки О2 на схеме механизма (см. рис. 34). На плане ускорений (см. рис. 35) вектор
) направлен из точки В к точки О2 на схеме механизма (см. рис. 34). На плане ускорений (см. рис. 35) вектор 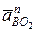 изобразится из точки
изобразится из точки  , длина
, длина 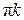 составит
составит
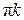 =
= 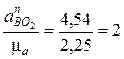 мм.
мм.
Вектор ускорения 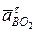 направлен из точки В перпендикулярно звену ВО2 на схеме механизма (
направлен из точки В перпендикулярно звену ВО2 на схеме механизма ( 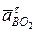 ÖВО2) (см. рис.34). На плане ускорений (см. рис. 35) из точки k изображаем линию, вдоль которой направлен вектор ускорения
ÖВО2) (см. рис.34). На плане ускорений (см. рис. 35) из точки k изображаем линию, вдоль которой направлен вектор ускорения 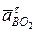 .
.
В пересечении двух линий ( 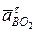 ÖВО2) и (
ÖВО2) и ( 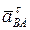 ÖВА) определяем точку b (см. рис. 35).
ÖВА) определяем точку b (см. рис. 35).
Численное значение вектора ускорения точки В составит ( 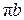 составит 32,4 мм)
составит 32,4 мм)
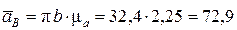 см/с2.
см/с2.
Для изображения вектора ускорения точки В (  ) на схеме механизма, требуется вектор
) на схеме механизма, требуется вектор 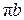 с плана ускорений (см. рис.35) параллельно перенести в точку В механизма (см. рис.34).
с плана ускорений (см. рис.35) параллельно перенести в точку В механизма (см. рис.34).
Поскольку звено АВ приобретает угловое ускорение 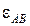 относительно неподвижной точки А под действием касательного ускорения точки В относительно точки А (
относительно неподвижной точки А под действием касательного ускорения точки В относительно точки А ( 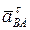 ), то для определения модуля ускорения
), то для определения модуля ускорения 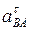 необходимо на плане ускорений (см. рис.35) измерить отрезок lb и умножить на масштаб плана ускорений
необходимо на плане ускорений (см. рис.35) измерить отрезок lb и умножить на масштаб плана ускорений 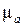 (lb составит 7,25 мм).
(lb составит 7,25 мм).
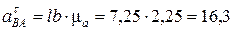 см/с2.
см/с2.
Для изображения вектора ускорения 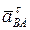 из точки В на схеме механизма требуется вектор lb с плана ускорений (см. рис.35) параллельно перенести в точку В механизма (см. рис.34).
из точки В на схеме механизма требуется вектор lb с плана ускорений (см. рис.35) параллельно перенести в точку В механизма (см. рис.34).
Тогда угловое ускорение 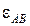 звена АВ относительно центра вращения точки А под действием вектора ускорения
звена АВ относительно центра вращения точки А под действием вектора ускорения 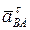 направлено против часовой стрелки на схеме механизма (см. рис.34). Определим численное значение углового ускорения
направлено против часовой стрелки на схеме механизма (см. рис.34). Определим численное значение углового ускорения 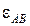
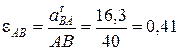 с-2.
с-2.
5.1.3. Определим ускорение точки М ( 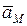 ).
).
Поскольку точка М принадлежит звену АВ (при этом известно ускорение точек А и В), то ускорение точки М можно определить методом обхода точек на плане ускорений. Точка М делит звено АВ пополам, следовательно, на плане ускорений точка m рассекает отрезок аb по середине (рис.35). На плане ускорений вектор точки 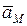 изобразится вектором
изобразится вектором 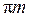 . Численное значение ускорения точки М составит (
. Численное значение ускорения точки М составит ( 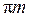 равен 46,2 мм)
равен 46,2 мм)
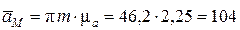 см/с2.
см/с2.
Для изображения вектора ускорения 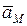 из точки М на схеме механизма требуется вектор
из точки М на схеме механизма требуется вектор 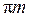 с плана ускорений (см. рис.35) параллельно перенести в точку М механизма (см. рис.34).
с плана ускорений (см. рис.35) параллельно перенести в точку М механизма (см. рис.34).
5.2. Методом мгновенного центра ускорений (МЦУ)
5.2.1.Определим положение МЦУ звена АВ.
Ускорение точки А (  ) определяется по пункту 5.1.1, изобразим на схеме (рис. 36). Укажем угловую скорость и угловое ускорение звена АВ,
) определяется по пункту 5.1.1, изобразим на схеме (рис. 36). Укажем угловую скорость и угловое ускорение звена АВ, 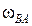 и
и  , соответственно, относительно полюса точки А.
, соответственно, относительно полюса точки А.
