Дифференциальных уравнений

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ ПО ДИСЦИПЛИНЕ

«Прикладная математика»

На тему: « Дифференциальные уравнения»

для направления:

23.03.01 « Технология транспортных процессов»

Челябинск

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К РЕШЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ ПО ОБЫКНОВЕННЫМ ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ

ВВЕДЕНИЕ

Математический аппарат дифференциальных уравнений нередко используется в экономике для описания поведения модели экономического процесса, например, балансовой модели, включающей расходную и доходную часть экономики. Основой этих моделей является допущение о непрерывности функций, отражающих процессы. Решение дифференциальных уравнений поведения экономической модели дает полную и качественную информацию для анализа экономического процесса, позволяет изменять его параметры и влиять на конечный результат процессов.

Поэтому обучающийся должен знать основные понятия теории дифференциальных уравнений, уметь составлять дифференциальные уравнения и знать основные способы их решения.

Контрольная работа состоит из:

1. Контрольных вопросов по теории обыкновенных дифференциальных уравнений.

2. Практических задач на темы:

· Составление дифференциальных уравнений;

· Существование и единственность решения дифференциального уравнения;

· Качественный анализ дифференциального уравнения;

· Решение дифференциального уравнения с разделяющимися переменными;

· Решение линейного неоднородного дифференциального уравнения 1-го порядка;

· Решение линейного неоднородного дифференциального уравнения 2-го порядка.

В процессе изучения темы необходимо усвоить принцип составления дифференциального уравнения и обратить внимание на соответствие одного и того же дифференциального уравнения процессам различной природы.

Следует хорошо усвоить понятие общего и частного решения обыкновенного дифференциального уравнения (ОДУ). Понять графическое представления интегральной кривой, т.е. уметь строить поле направлений и представлять в нем семейство интегральных кривых.

Обучающийся должен понимать, что решение ОДУ существует не всегда и уметь находить условия его существования и особые решения. Кроме того, надо понимать, что даже для составленного дифференциального уравнения какого-нибудь процесса не всегда можно найти решение. В этом случае используются методы качественного анализа решения ОДУ, которыми также обучающийся должен владеть, уметь строить фазовые портреты для ОДУ.

Небольшой набор методов решений ОДУ, рассматриваемых по данной дисциплине включает в себя:

· Метод разделения переменных;

· Метод подстановки;

· Метод вариации произвольных постоянных;

· Метод подбора частного решения.

Используя эти методы, обучающийся должен уметь решать дифференциальные уравнения:

· Однородные;

· Линейные 1-го порядка, однородные и неоднородные;

· Линейные 2-го порядка, однородные и неоднородные, с постоянными коэффициентами.

При этом обучающийся должен усвоить приемы понижения порядка ОДУ в простейших случаях, знать, что такое характеристическое уравнение для однородного линейного уравнения и уметь находить решения неоднородных ДУ как сумму общего решения однородного ДУ и частного решения неоднородного ДУ.

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ

КОНТРОЛЬНЫХ ЗАДАНИЙ

При выполнении контрольной работы необходимо придерживаться

следующих правил:

1. Обучающийся обязан делать контрольную работу только своего варианта в сроки, предусмотренные графиком.

2. Номер варианта определяется по списку группы в ведомости.

3. Контрольную работу следует выполнять аккуратно либо в ученической

тетради чернилами любого цвета, кроме красного, оставляя поля (3 – 4 см) для замечаний рецензента, либо на листах формата А-4.

Рекомендуется в конце тетради указать список используемой литературы и оставить несколько чистых листов для исправлений и дополнений в соответствии с указаниями рецензента .

4. На обложке тетради обучающийся должен указать свою фамилию, имя,

отчество, также название работы, номер варианта, форму обучения,

направление, курс, номер группы, домашний адрес и дату отправки

(титульный лист как образец есть в дисках).

5. Перед решением задачи нужно полностью выписать ее условие. Если

несколько задач имеют общую формулировку, переписывать следует только

условие задачи нужного варианта. Решение каждой задачи следует

сопровождать подробными ссылками на соответствующие формулы, теоремы и правила. Вычисления должны быть доведены до конечного числового результата. Ответы и выводы, полученные при решении задач, следует подчеркнуть.

6. После получения отрецензированной работы обучающемуся необходимо

исправить все отмеченные ошибки и недочеты.

7. Если работа возвращена на доработку, то следует переделать те задачи,

на которые указывает рецензент, а при отсутствии такого указания контрольная работа должна быть выполнена заново.

Переделанная работа высылается на повторное рецензирование обязательно с незачтенной ранее работой и рецензией к ней. При этом на обложке следует указать фамилию рецензента.

8. Работы, выполненные без соблюдения этих правил, к зачету не

принимаются и возвращаются без рецензирования для переработки.

9. На экзамен допускаются обучающиеся, контрольная работа которых

является зачтенной.

Номер варианта обучающегося соответствует номеру по списку в ведомости!!!

I. Вопросы по теории обыкновенных

дифференциальных уравнений

1. Что называется обыкновенным ДУ. Привести пример обыкновенного ДУ и уравнения в частных производных. Порядок ОДУ. Однородное и неоднородное ОДУ.

2. Общее и частное решение ОДУ. Задача Коши для ОДУ.

3. Теорема о существовании и единственности решения ОДУ 1-го порядка 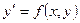. Геометрический смысл теоремы.

4. Автономное дифференциальное уравнение. Стационарные точки. Области убывания и возрастания интегральных кривых. Неподвижные точки.

5. Понятие фазового портрета автономного ОДУ.

6. Общее решение ОДУ видов 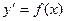и .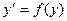

7. Что такое однородная функция степени k, однородное ОДУ и каким методом оно решается?

8. Что такое линейное ОДУ. Метод его решения

9. Какой подстановкой решается ОДУ 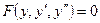? Метод понижения порядка ОДУ.

10.Линейное ОДУ. Свойства линейных ОДУ.

11.Линейное ОДУ 2-го порядка. Однородное ЛОДУ. Характеристическое уравнение. Общее решение однородного ЛОДУ.

12.Метод подбора частного решения для неоднородного ЛОДУ 2-го порядка.

13.Метод вариации производной постоянной для неоднородного ЛОДУ 2-го порядка.

14.Какой вид должно иметь частное решение неоднородного ЛОДУ 2-го порядка, если:

1. λ=в это один из корней характеристического уравнения, а правая часть ЛОДУ имеет вид а+вх.

2. λ=в это один из корней характеристического уравнения, а правая часть ЛОДУ имеет вид .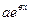

3. λ_1,2=+вi – это корни характеристического уравнения, а правая часть ЛОДУ имеет вид .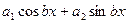

4. λ=0 – это квадратный корень характеристического уравнения, а правая часть ЛОДУ имеет вид а + вх.

5. λ = в – это кратный корень характеристического уравнения, а правая часть ЛОДУ имеет вид а + вх.