Метод половинного деления

Решение трансцендентных и алгебраических уравнений

Трансцендентное уравнение - это уравнение, содержащее трансцендентные функции (показательные, логарифмические, тригонометрические и обратные тригонометрическим) от неизвестного (переменного).

Например, уравнение

.

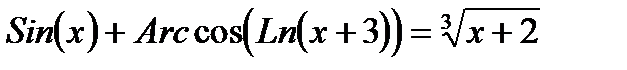Алгебраическим уравнением степени n, в свою очередь, называется уравнение вида

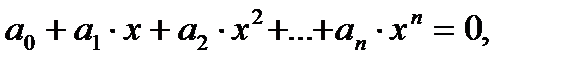
где 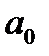, ..., 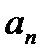- некоторые вещественные числа, причем .

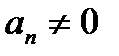Трансцендентные и алгебраические уравнения, в общем случае, можно решать только приближенно. Поэтому особое значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности.

Постановка задачи

Пусть дано уравнение 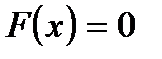, где функция F(x) определена и непрерывна в некотором конечном или бесконечном интервале a<x<b.

Если в дальнейшем потребуется существование и непрерывность первой производной 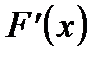или второй производной 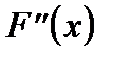, то данные требования будут также оговорены.

Мы будем предполагать, что уравнение 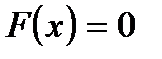имеет лишь изолированные корни, т.е. для каждого корня уравнения существует некоторая окрестность, не содержащая других корней уравнения.

Приближенное нахождение изолированных действительных корней состоит из двух этапов:

1. Отделение корней, т.е. установление по возможности малых промежутков 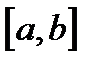, в каждом из которых содержится один и только один корень уравнения.

2. Уточнение приближенного корня, т.е. его определение с заданной точностью.

Для первого этапа рекомендуется применять следующую теорему из математического анализа:

Теорема. Если непрерывная функция 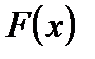принимает значения разных знаков на концах отрезка 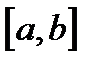, т.е. 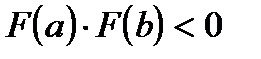, то внутри этого отрезка содержится, по крайней мере, один корень уравнения 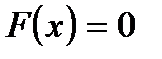, т.е. 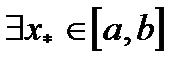, такой что .

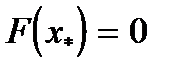Примечание. Корень 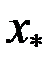будет единственным, если производная 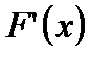существует и сохраняет постоянный знак внутри интервала .

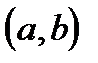Следовательно, первый этап заключается в определении отрезка 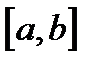, на концах которого функция 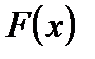имеет значения разных знаков[1]. Для выполнения первого этапа применяют либо графический способ, либо перебор точек разбиения отрезка. Построение графика функции является, в общем случае, не самым эффективным способом для выполнения первого этапа, т.к. данный процесс сам представляет собой достаточно сложную задачу. Его применяют на компьютерах, если для построения графика функций используется или известный профессиональный пакет программ (типа Grapher), или специально разработанная «самодельная» программа. Второй способ - перебор точек - заключается в следующем. Берут достаточно большой отрезок 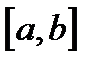, разбивают его на несколько (например, порядка 10) частей. Вычисляют значения функции во всех точках разбиения. В качестве предварительного решения берут тот отрезок, на концах которого функция имеет разные знаки.

Пример. Нижеприведенная программа находит отрезок, на котором уравнение 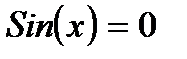имеет изолированный корень.

Program Perebor;

Const N=10; {На сколько частей разбить отрезок}

Var A,B,x1,x2,h:Real; i:Integer;

Function F(X:real):real;

begin

{Задаем функцию уравнения}

F:=Sin(x);

end;

begin {Начало программы}

Writeln(’Введите координаты отрезка A,B’);

Readln(A,B);

{Вычисляем длину частичного отрезка}

h:=(B-A)/N;

{Разбиваем отрезок на N частей}

For i:=1 to N do

begin

{Левая координата отрезка}

x1:=A+h*(i-1);

{Правая координата отрезка}

x2:=A+h*i;

{Если на границах отрезка значения}

{разных знаков, то сообщаем о}

{найденном изолированном корне}

If F(x1)*F(x2)<=0 then

Writeln(’ На отрезке от ’,x1:12:7,

’ до ’,x2:12:7,

’ есть корень’);

end;

{Задержка окна результатов на экране}

Readln;

end.

Также на первом этапе рекомендуется проверить, что в найденном отрезке находится только один изолированный корень. Для алгебраических уравнений можно использовать следующую теорему.

Основная теорема алгебры. Алгебраическое уравнение степени n имеет ровно n корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность.

Поэтому, если для алгебраического уравнения мы нашли n отрезков, на которых функция меняет знак, то мы изолировали все корни.

Для выполнения второго этапа - нахождения изолированного корня с заданной точностью - применяют специальные методы вычислительной математики. Данные методы можно условно разбить на две группы - первые получают решение в виде предела последовательности отрезков, содержащих изолированный корень. Ниже представлены два подобных метода - метод половинного деления и метод хорд. Вторые представляют корень уравнения в виде предела последовательности приближенных корней разной (увеличивающейся) степени точности. Примеры методов - метод итераций, метод Ньютона, модифицированный метод Ньютона и метод секущих.

Необходимо также отметить, что большинство из приведенных методов работают только для корней кратности 1. Если на отрезке существует корень кратности 2 или большей, то для их нахождения следует использовать метод Ньютона с параметром.

Метод половинного деления

Пусть дано уравнение

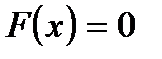, (1.1)

где функция F(x) определена и непрерывна на отрезке 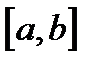, причем .

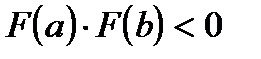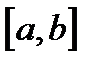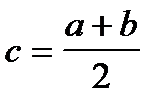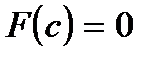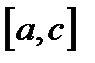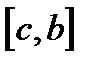Метод половинного деления заключается в следующем. Делим отрезок пополам. Вычисляем . Если , то с - корень уравнения. Мы получили решение задачи, и работа прекращается. В противном случае, выбираем в качестве очередного один из отрезков или , на границах которого функция имеет значения разных знаков (т.е. именно в нем остался корень). Этот отрезок переобозначаем через 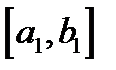, снова делим пополам и т.д. Данный процесс повторяем до тех пор, пока длина очередного отрезка не станет меньше заданной погрешности Eps (например, Eps=0.001). В этом случае, в качестве приближенного значения корня берут середину последнего отрезка .

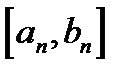Проверим сходимость метода. Последовательность 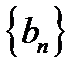- невозрастающая ограниченная снизу последовательность. Следовательно, она имеет предел 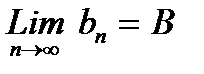. Аналогично, последовательность 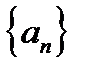является неубывающей ограниченной сверху последовательностью и поэтому имеет свой предел 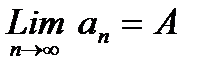. Из условий 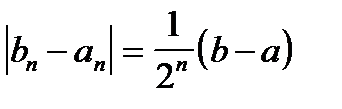и существования двух пределов получаем, что A=B. Причем, из условия 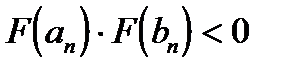, переходя к пределу при 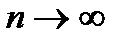, получаем, что 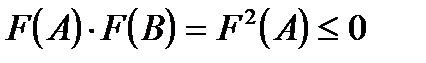и, следовательно, 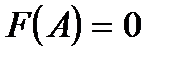. Итак, метод половинного деления сходится к корню уравнения.

Пример. Ниже приведен фрагмент программы, выбирающий очередной отрезок для метода половинного деления.

{Вычисляем середину отрезка}

C:=(A+B)/2;

{Если на [a,c] значения функции разных знаков,}

{то выбираем этот отрезок для продолжения,}

{иначе продолжаем работать с отрезком [c,b]}

If F(A)*F(C)<0 then B:=C else A:=C;

Выбор очередного отрезка с корнем необходимо выполнять несколько раз, до тех пор, пока его длина не будет меньше погрешности Eps. Следовательно, для организации данного процесса необходим цикл. Т.к. заранее неизвестно, сколько раз необходимо выполнить данную операцию, то оператор цикла For ... To ... Do не подходит. Зато известен критерий (условие) окончания процесса. Поэтому для программы метода половинного деления рекомендуется использовать оператор цикла с постусловием Repeat ... Until.

Пример. Ниже приведен фрагмент программы, организующий выбор отрезка в цикле.

{Начинаем цикл с постусловием}

Repeat

{Здесь находятся команды выбора}

{очередного отрезка}

...

{Проверяем критерий окончания счета}

Until Abs(B-A)<Eps;

{Все, корень найден.}

{Выводим его значение на экран.}

Недостаток метода половинного деления - его медленная сходимость. Если функция уравнения имеет сложный вид и ее значение вычисляется относительно долго, то для нахождения корней рекомендуется применять другие методы. В профессиональных программах метод деления отрезка пополам обычно используют только для грубого нахождения корней.

Метод хорд

Метод хорд также называется методом пропорциональных частей. Его алгоритм основан на алгоритме метода половинного деления. Но для разбиения исходного отрезка на две части используется не его середина, а иная точка. Методом хорд обычно получают решение за меньшее количество делений отрезка.

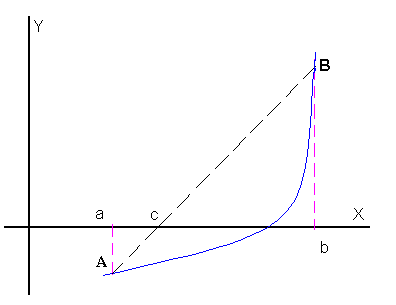Рисунок 1. Геометрический смысл метода хорд

Пусть для простоты 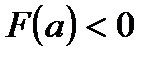, а 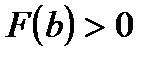. Тогда, вместо того, чтобы делить отрезок пополам, его делят в отношении - 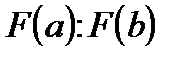. Это дает нам точку 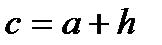, где 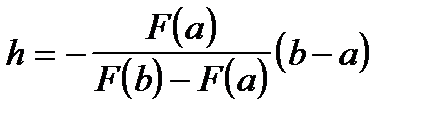. Далее выбираем один из отрезков 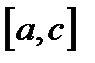или 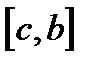, на котором функция имеет значения разных знаков.

Геометрический смысл метода пропорциональных частей (см. рисунок № 1) эквивалентен замене кривой 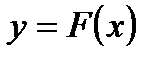хордой, проходящей через точки A 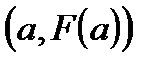и B 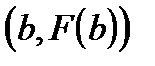. В самом деле, уравнение хорды AB есть 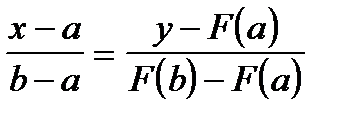. Положим 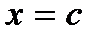и 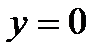, получим

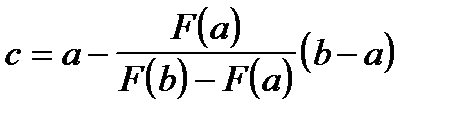. (1.2)

Если же 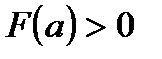, а 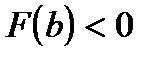, то формула вычисления значения 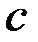остается прежней (но меняется рисунок № 1).

Можно также пользоваться формулой хорд

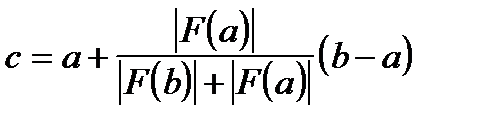, (1.3)

где - знак модуля.

Сходимость метода хорд можно доказать, если потребовать, чтобы вторая производная 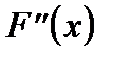сохраняла свой знак на отрезке .

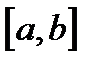Примечание. В программе перед командами методов половинного деления и хорд рекомендуется вставить команды проверки корректности начального определения отрезка для поиска корня. Значения на границах указанного отрезка должны быть разных знаков. Иначе программа работать не будет, если случайно ошиблись с начальным отрезком. Программа может «зависнуть» или «зациклится».

Пример. Ниже приведен фрагмент программы. Если ранее указанный отрезок не подходит, выдается соответствующее сообщение и программа прекращает свою работу.

{если на границе значения одного знака}

If F(A)*F(B)>0 then

begin

{На экран выводим соответствующее сообщение}

Writeln(’На отрезке от ’,A:12:7,’ до ’,B:12:7,

’ корней нет’);

{Прекращаем работу программы}

Halt(1);

end;

Метод итераций

Пусть дано уравнение

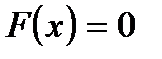. (1.4)

Умножим обе части уравнения на некоторую функцию 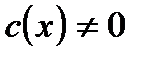[2], и прибавим 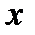к обеим частям уравнения. Получим тождественное уравнение

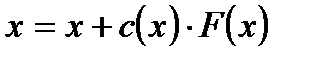. (1.5)

Обозначим

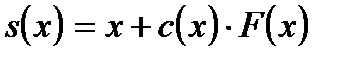. (1.6)

Следовательно, от уравнения (1.4) мы переходим к тождественному уравнению (1.7)[3]:

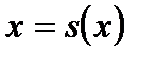. (1.7)

Выберем каким-нибудь образом грубое приближенное значение корня 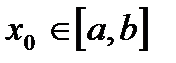(например, один из концов отрезка). Назовем его начальным приближением. Подставим 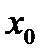в правую часть нового уравнения (1.7) и вычислим очередное приближение 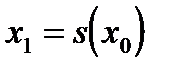. Далее подставим 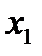в правую часть уравнения (1.7) и вычислим 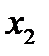. Будем повторять данный процесс. В результате получим последовательность значений:

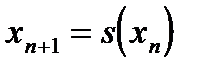, где 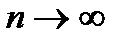. (1.8)

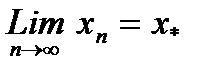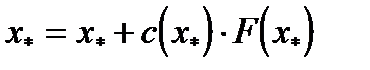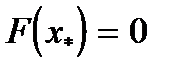Если данная последовательность сходится, т.е. у нее существует предел , то, перейдя к пределу, получим и . Следовательно, 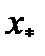- корень уравнения. Т.к. на компьютерах практически невозможно проводить бесконечно большое количество операций (т.к. это потребует бесконечно большого количества машинных часов), то точное значение корня вычислить, в общем случае, нельзя. Но приближенное значение корня можно вычислить с любой требуемой точностью.

Как определить, сколько раз необходимо выполнить итерационную формулу 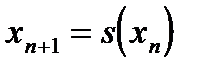, и с какой точностью будет найден приближенный корень? На практике задают погрешность Eps (обычно Eps=0.001) и говорят, что требуемая точность достигнута при выполнении одного из услови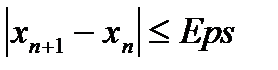й: или 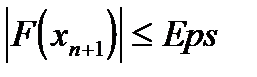. Данные условия окончания счета принято называть критериями сходимости. Иногда в качестве критерия пытаются использовать выполнение определенного заранее заданного количества итераций[4]. Но указанный третий подход на практике является неверным и может быть использован только в качестве защиты от зацикливания программы при неверных исходных параметрах.

Теоретическим обоснованием метода итераций служит следующая теорема.

Теорема. Пусть функция 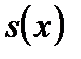определена и дифференцируема на отрезке 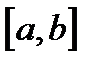, причем все ее значения 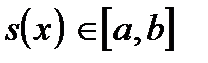. Тогда, если существует рациональное число q, такое что 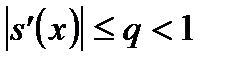для 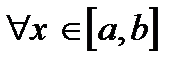, то 1) Процесс итерации 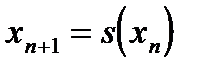для 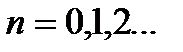сходится независимо от начального значения 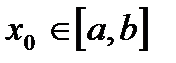. 2) Предельное значение 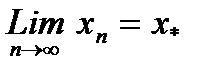является единственным корнем уравнения .

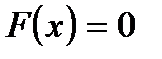Примечание. На практике обычно берут константу 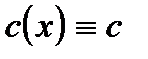и используют итерационный процесс 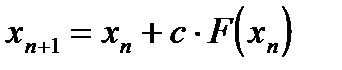. Следовательно, 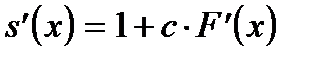и метод итераций сходится при условии .

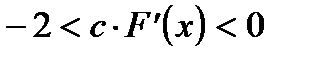Пример. Решить уравнение .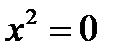

Берем const 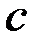. Получаем .

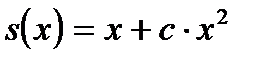Далее, .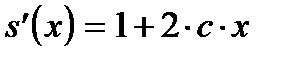

Согласно условиям теоремы и примечания имеем .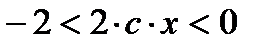

Т.к. для любого отрезка, содержащего корень уравнения 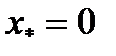, данное условие выполняться не будет (невозможно подобрать const c), то теоретически метод итераций для этого примера сходиться не будет при любом начальном приближении. Однако на практике возможно подобрать коэффициенты метода итераций для его сходимости. Например, пр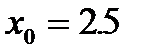и и 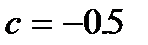метод не сходится. Пр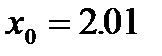и и 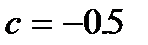метод сходится при погрешности Eps=0.0001 и уже не сходится при Eps=0.00001.

Пример. Решить уравнение .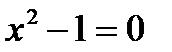

В качестве отрезка с корнем возьмем .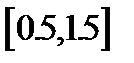

Берем const c. Получаем .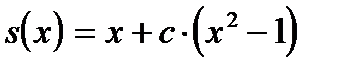

Далее, .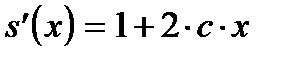

Согласно условиям теоремы и примечания имеем .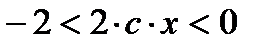

При 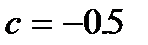вышеприведенное неравенство верно для заданного отрезка и метод итераций сходится при любом начальном приближении из отрезка .

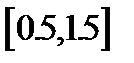Пример. Ниже приведен фрагмент программы, реализующий метод итераций. Для реализации последовательности приближений используется цикл с постусловием Repeat ... Until. Считается, что все нужные переменные и функция F(x) ранее определеныи им заданы нужные значения.

{Задаем начальное приближение}

Xn:=X0;

{Начинаем цикл с постусловием}

Repeat

{Вычисляем очередное приближение}

Xn1:=Xn-C*F(Xn);

{Очередное приближение становится предыдущим}

Xn:=Xn1;

{Проверяем критерий сходимости - конец цикла}

Until Abs(F(Xn1))<Eps;

{Выводим приближенное значение корня Xn1 на экран}

Для оценки погрешности приближенного значения корня можно использовать следующее неравенство

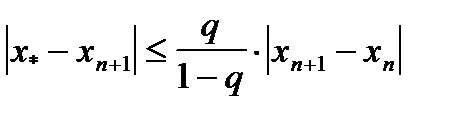. (1.9)

Метод Ньютона

Пусть корень 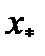уравнения 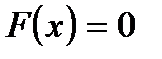является изолированным корнем на отрезке 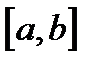, причем первая производная 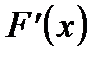и вторая производная 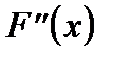непрерывны и сохраняют определенные знаки при .

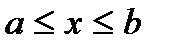Если известно некоторое приближение решения 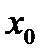, то его можно уточнить методом Ньютона.

Для вывода формулы метода Ньютона используем формулу Тейлора. Имеем

.

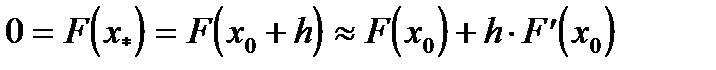Поэтому

.

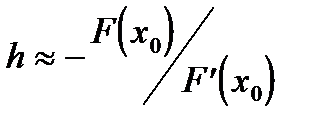Положим

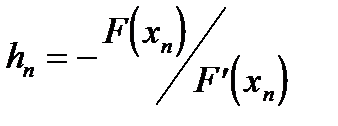(1.10)

и построим итерационный процесс

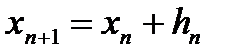. (1.11)

Итак, метод Ньютона имеет следующую формулировку. Выберем начальное приближение 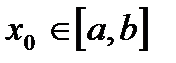. Найдем очередные приближения по формуле

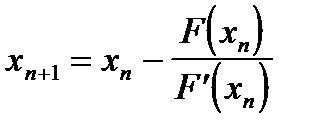, n=0,1,2... (1.12)

Критерии окончания расчетов для метода Ньютона аналогичны критериям метода итераций (приведены выше).

Теоретическое обоснование метода Ньютона заключено в следующей теореме.

Теорема. Если 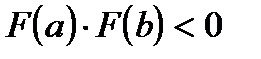, причем первая производная 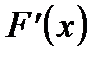и вторая производная 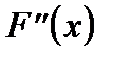непрерывны, отличны от нуля и сохраняют определенные знаки при 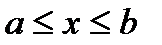, то, исходя из начального приближения 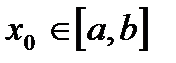, удовлетворяющего неравенству 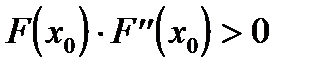, можно вычислить методом Ньютона корень уравнения с любой степенью точности.

Примечание. В качестве исходной точки 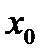можно выбрать тот конец интервала 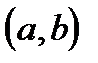, которому отвечает ордината того же знака, что и .

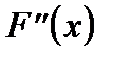Примечание. Алгоритмы программ методов итераций и Ньютона практически совпадают, только очередные приближения 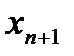вычисляются по разным формулам.

На практике для итерационных методов с первого раза трудно подобрать хорошее начальное приближение. Так, сходимость метода Ньютона сильно зависит от правильного выбора начального приближения. В случае его неверного выбора, ошибки в алгоритме или реализации неподходящего метода (у каждого метода есть свои определенные условия для решаемой задачи) программа обычно зацикливается или прекращает работу с ошибкой. Поэтому в программу для любого из итерационных методов рекомендуется вставить счетчик итераций, т.е. ввести специальную переменную. При вычислении очередного приближения (выполнена одна итерация) увеличивать значение этой переменной на единицу. Когда значение этой переменной превзойдет заранее заданное максимальное значение (для метода Ньютона обычно используют число 30), программа прекращает работу с выдачей соответствующего сообщения.

Пример. Ниже представлен фрагмент программы со счетчиком итераций Iter. Когда значение больше 30, программа прекращает свою работу.

{Задаем начальное значение счетчика итераций}

Iter:=0;

{начинаем цикл метода}

Repeat

{Вычисляем очередное приближение}

Xn1:=...

...

{Увеличиваем значение счетчика итераций}

Iter:=Iter+1;

{Если его значение превосходит максимально}

{заданное, даем сообщение и заканчиваем работу}

If Iter>30 then

begin

Writeln(’Корень уравнения не найден’);

Halt(1);

end;

{конец цикла и проверка критерия сходимости}

Until Abs(F(Xn1))<Eps;

Примечание. Метод Ньютона удобно применять в том случае, когда в окрестности корня график функции имеет большую кривизну (т.е. значение производной 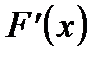велико). В противном случае метод сходится долго и его применение не рекомендуется.

приближения. Поэтому метод Ньютона при решении сложных прикладных задач используют в качестве второго дополнительного метода. Например, методом половинного деления находят приближенный корень с погрешностью 0.1, а затем методом Ньютона «уменьшают» погрешность до 0.0000001

Геометрический смысл метода Ньютона (см. рисунок № 2) заключается в замене кривой 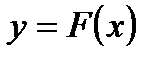касательной, проведенной в некоторой точке кривой. Выбирается начальное приближение 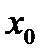. Проводится касательная к кривой в точке 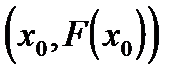. Абсцисса точки пересечения касательной и оси Ох берется за очередное приближение 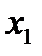. Далее снова проводится касательная в точке 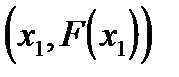и т.д. Из уравнения касательной и данного алгоритма можно также вывести формулу метода Ньютона.

Если на 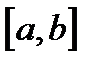существует изолированный корень 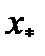с кратностью p, то условие 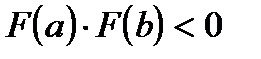может и не выполняться (при четной кратности). В этом случае, следует использовать вариант метода Ньютона с параметром для кратных корней:

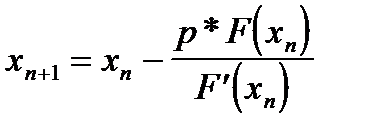. (1.15)