Применение теоремы Виета и исследование расположения корней квадратного уравнения относительно нуля
Самым мощным инструментом при решении сложных задач с параметрами является теорема Виета. Но здесь нужно быть предельно внимательным к формулировке.
Этих двух теорем ( прямой и обратной )
Теорема Виета
Если уравнение 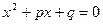 имеет корни и
имеет корни и 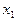 ;
; 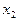 то выполнены равенства
то выполнены равенства 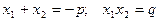 .
.
Особенности теоремы:
Первое. Теорема верна только для уравнения 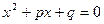 и не верна для
и не верна для
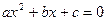
В последнем случае нужно сначала разделить обе части уравнения на ненулевой коэффициент а при х2, а потом уже применять теорему Виета.
Второе. Для использования результатов теоремы необходимо иметь факт существования корней уравнений т.е. не забывать наложить условие D>0
Обратная
Теорема Виета
Если есть произвольные числа и то они являются корнями уравнения
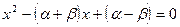
Очень важное замечание, облегчающее решение задач: обратная теорема гарантирует существование корней в уравнении что позволяет не возится с дискриминантом. Он автоматически в этом случае неотрицателен.
Рекомендации для учащихся
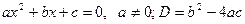
| Условия на корни | Равносильное условие на коэффициенты а,в,с, и дискриминант D | |
Корни 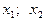 существуют ( и различны) существуют ( и различны) | 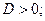 | |
Корни существуют и равны 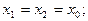 Причем Причем 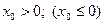 | 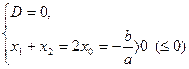 | |
Корни существуют и 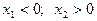 |  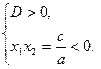 | |
Корни существуют и 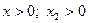 | 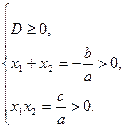 | |
Корни существуют и различны 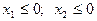 | 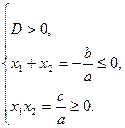 | |
Корни существуют, один корень равен нулю, а другой >0 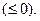 | 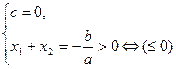 |
1). Установить, при каких значениях параметра 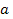 уравнение
уравнение 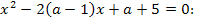
Не имеет корней.
Если уравнение не имеет корней, то необходимо и достаточно, чтобы дискриминант 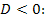
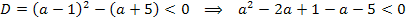
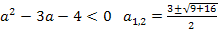 =
= 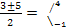
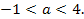
имеет различные положительные корни.
Раз корни есть, то 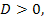 если они оба положительные, то
если они оба положительные, то 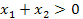 и
и 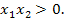 Воспользуемся формулой Виета, тогда для данного уравнения
Воспользуемся формулой Виета, тогда для данного уравнения
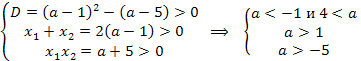 ⟹
⟹ 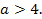
Имеет различные отрицательные корни
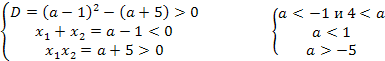
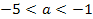
Имеет корни разного знака
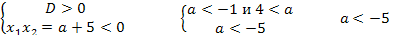
Имеет совпадающие корни
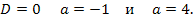
2). При каких значениях параметра а оба корня квадратного уравнения 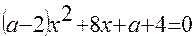 будут положительными?
будут положительными?
Решение.
Так как заданное уравнение является квадратным, то 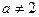 оба его корня (равные или различные) будут положительными, если дискриминант неотрицателен, а сумма и произведение корней положительны, то есть
оба его корня (равные или различные) будут положительными, если дискриминант неотрицателен, а сумма и произведение корней положительны, то есть
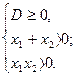
Так как, 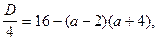 а по теореме Виета,
а по теореме Виета,
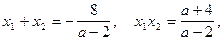
То получим систему неравенств
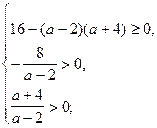
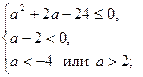
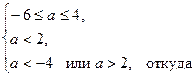
Ответ: 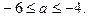
3). Найти все значения параметра а, при которых корни квадратного уравнения 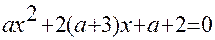 неположительны.
неположительны.
Решение.
Так как заданное уравнение является квадратным, то 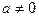 . Оба его корня (равные или различные) будут отрицательными или равными нулю, если дискриминант неотрицательный, сумма корней отрицательна или равна нулю, а произведение корней неотрицательно, то есть
. Оба его корня (равные или различные) будут отрицательными или равными нулю, если дискриминант неотрицательный, сумма корней отрицательна или равна нулю, а произведение корней неотрицательно, то есть
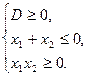
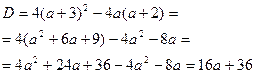
а по теореме Виета
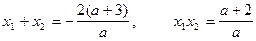
то получим систему неравенств.
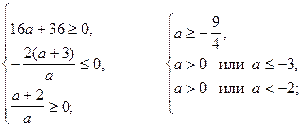 откуда
откуда 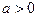
Ответ: 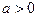
4).При каких значениях параметра а сумма квадратов корней уравнения 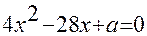 равна 22.5 ?
равна 22.5 ?
Решение.
Вначале предложим “ решение “, с которым нам не раз приходилось встречаться.
Имеем 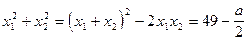
поскольку 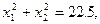 то получаем “Ответ”
то получаем “Ответ” 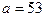 Однако при найденном значении а исходное уравнение корней не имеет.
Однако при найденном значении а исходное уравнение корней не имеет.
В этом решении мы столкнулись с одной из “популярнейших” ошибок, связанной с применением теоремы Виета:
вести речь о корнях предварительно не выяснив, существуют они или нет.
Так, в данном примере, в первую очередь необходимо было установить, что лишь при 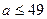 исходное уравнение имеет корни. Только после этого можно обратится к выкладкам, приведенным выше.
исходное уравнение имеет корни. Только после этого можно обратится к выкладкам, приведенным выше.
Ответ: Таких а не существует.
5). Корни уравнения 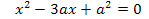 таковы, что
таковы, что 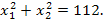 Определить
Определить 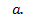
Решение. По теореме Виета 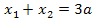
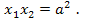 Возведем обе части первого равенства в квадрат
Возведем обе части первого равенства в квадрат 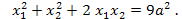 Учитывая, что
Учитывая, что 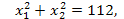 а
а 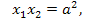 получаем
получаем 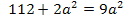 или
или 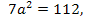
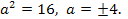 Проверка показывает, что значения
Проверка показывает, что значения 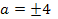 удовлетворяют исходному уравнению.
удовлетворяют исходному уравнению.
Ответ: 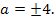
6).При каком значении параметра а сумма квадратов корней уравнения 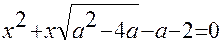 принимает наименьшее значение:
принимает наименьшее значение:
Решение.
Найдем дискриминант данного уравнения. Имеем 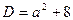 Здесь важно не сделать ошибочный вывод о том, что уравнение имеет два корня при любом а. оно действительно имеет два корня при любом, но допустимом а, т.е. при
Здесь важно не сделать ошибочный вывод о том, что уравнение имеет два корня при любом а. оно действительно имеет два корня при любом, но допустимом а, т.е. при 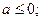 при
при 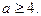
Используя теорему Виета, запишем
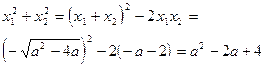
Таким образом, для получения ответа осталось найти наименьшее значение квадратичной функции 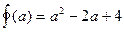
на множестве 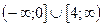
Поскольку при 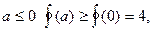 а при
а при 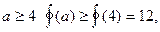 то функция
то функция 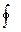 на указанном множестве принимает наименьшее значение в точке
на указанном множестве принимает наименьшее значение в точке 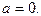
Ответ: 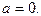
Задачи для самостоятельного решения
1). Найти все значения параметра а, при которых корни квадратного уравнения
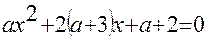
неотрицательны
Ответ: 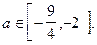
2). Вычислить значение выражения 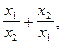 ,где
,где 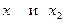 -корни уравнения
-корни уравнения 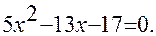
Ответ: 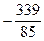
3). Найти все значения параметра а, при которых сумма квадратов действительных корней уравнения 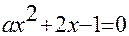 больше 6.
больше 6.
Ответ: 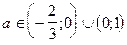
4).При каких значениях параметра а уравнение ах2-4х+а=0 имеет:
а) положительные корни
б) отрицательные корни
Расположение корней квадратичной функции относительно
заданных точек.
Для подобных задач характерна следующая формулировка: при каких значениях параметра корни ( только один корень ) больше (меньше, не больше, не меньше ) заданного числа А; корни расположены между числами А и В; корни не принадлежат промежутку с концами в точках А и В и т.п.
При решении задач, связанных с квадратным трехчленом
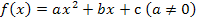 (1)
(1)
часто приходится иметь дело со следующими стандартными ситуациями (которые мы сформулируем в виде «вопрос – ответ».
Вопрос 1. Пусть дано число 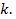 При каких условиях на коэффициенты квадратного трехчлена (1) оба его корня
При каких условиях на коэффициенты квадратного трехчлена (1) оба его корня 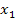 и
и 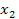 больше
больше 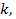 т.е.
т.е. 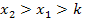 ?
?
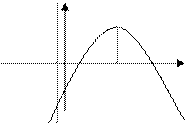
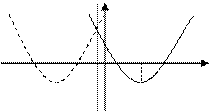
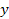
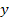
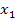
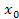
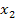
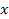
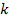
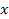
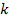
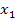
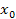
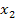
Рис.1
Ответ. Коэффициенты квадратного трехчлена (7) должны удовлетворять условиям
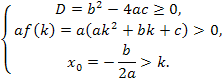
где 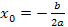 - абсцисса вершины параболы.
- абсцисса вершины параболы.
Справедливость сказанного вытекает из рис. 1, на котором отдельно представлены случаи 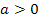 и
и 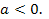 Отметим, что двух условий
Отметим, что двух условий 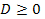 и
и 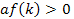 еще недостаточно, чтобы корни
еще недостаточно, чтобы корни 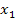 и
и 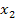 были больше
были больше 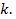 На первом из рис. 1 штрихом изображена парабола, удовлетворяющая этим двум условиям, но ее корни меньше
На первом из рис. 1 штрихом изображена парабола, удовлетворяющая этим двум условиям, но ее корни меньше 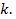 Однако, если к указанным двум условиям добавить, что абсцисса
Однако, если к указанным двум условиям добавить, что абсцисса 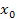 вершины параболы больше
вершины параболы больше 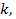 то и корни
то и корни 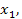
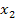 будут большими чем
будут большими чем 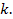
Вопрос 2. Пусть дано число 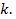 При каких условиях на коэффициенты квадратного трехчлена (1) его корни
При каких условиях на коэффициенты квадратного трехчлена (1) его корни 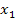 и
и 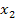 лежат на разные стороны от
лежат на разные стороны от 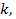 т.е.
т.е. 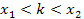 ?
?
Ответ. коэффициенты квадратного трехчлена (1) должны удовлетворять условию 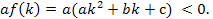
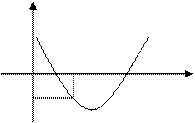
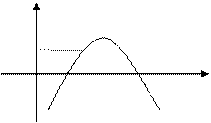
Справедливость сказанного вытекает из рис. 2, на котором отдельно представлены случаи 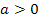 и
и 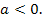 Отметим, что указанное условие гарантирует существование двух различных корней
Отметим, что указанное условие гарантирует существование двух различных корней 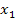 и
и 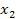 квадратного трехчлена (1).
квадратного трехчлена (1).
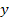
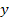
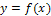
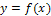
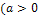 ) (
) ( 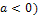
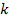
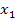
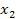
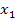
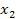
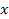
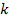
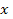
Рис. 2
Вопрос 3. При каких условиях на коэффициенты квадратного трехчлена (1) его корни 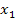 и
и 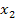 различны и только один из них лежит в заданном интервале
различны и только один из них лежит в заданном интервале 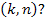
Ответ. Коэффициенты квадратного трехчлена (1) должны удовлетворять условию 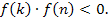
Вопрос 4. При каких условиях на коэффициенты квадратного трехчлена (1) множество его корней не пусто и все его корни 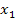 и
и 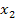 лежат в заданном интервале
лежат в заданном интервале 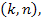 т.е.
т.е. 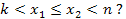
Ответ. Коэффициенты квадратного трехчлена (1) должны удовлетворять условиям
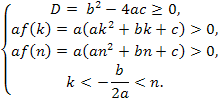
Для решения таких задач полезно работать с таблицей, которая приведена ниже.
Таблица
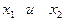 - корни многочлена
- корни многочлена 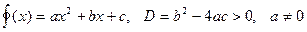
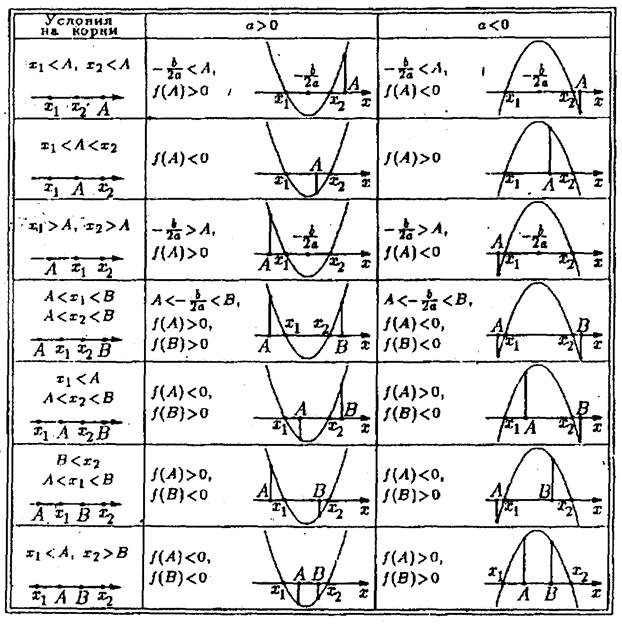
Задача 1. При каких значениях параметра 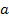 корни
корни 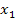 и
и 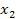 уравнения
уравнения
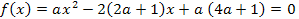
удовлетворяют условию 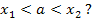
Решение. Воспользовавшись ответом на вопрос 2, получаем, что искомыми значениями параметра 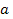 является множество решений неравенства
является множество решений неравенства
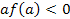 ⟺
⟺ 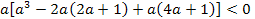 ⟺
⟺
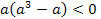 ⟺
⟺ 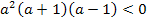 ⟺
⟺ 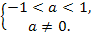
Ответ. 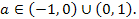
Задача 2. При каких значениях параметра 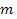 множество корней уравнения
множество корней уравнения
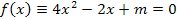
не пусто и все его корни принадлежат (-1, 1)?
Решение. Так как в предложенной задаче коэффициент при 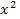 положителен, то воспользовавшись ответом на вопрос 4, получаем, что искомыми значениями параметра
положителен, то воспользовавшись ответом на вопрос 4, получаем, что искомыми значениями параметра 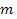 является множество решений следующей системы неравенств
является множество решений следующей системы неравенств
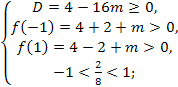 ⟺
⟺ 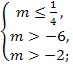 ⟺
⟺ 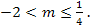
Ответ. 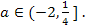
Задача 3. При каких значениях параметра 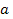 один из корней уравнения
один из корней уравнения
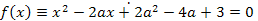
меньше 1, а другой – больше 2?
Решение. Так как в предложенной задаче коэффициент при 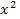 положителен, то, воспользовавшись ответом на вопрос 5, получаем, что искомыми значениями параметра
положителен, то, воспользовавшись ответом на вопрос 5, получаем, что искомыми значениями параметра 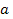 является множество решений следующей системы неравенств
является множество решений следующей системы неравенств
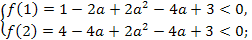 ⟺
⟺ 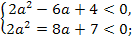 ⟺
⟺
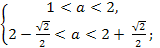 ⟺
⟺ 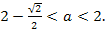
Ответ. 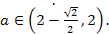
Задача4. Найти все значения параметра р, при которых оба корня квадратного уравнения 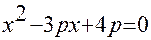 больше 2.
больше 2.
Решение.
Так как уравнение имеет два ( равных или различных ) действительных корня, то дискриминант 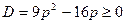
Как известно, графиком трехчлена 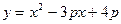 , стоящего в левой части уравнения, является парабола с ветвями, направленными вверх. А так же оба корня больше 2, то парабола пересекает ось 0х в точках, расположенных правее 2, а тогда получим, что
, стоящего в левой части уравнения, является парабола с ветвями, направленными вверх. А так же оба корня больше 2, то парабола пересекает ось 0х в точках, расположенных правее 2, а тогда получим, что 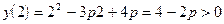 .
.
Вершина параболы также расположена правее 2, и, значит, ее абсцисса тоже будет больше 2, то есть 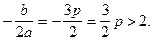
Таким образом, получим систему
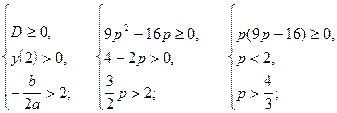
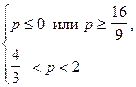
откуда
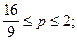
Ответ: 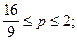
Задача5. Найти d, при которых корни уравнения 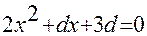 меньше 1.
меньше 1.
Решение:
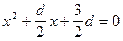 обратите внимание, на то что по условию корней может быть два или один. Поэтому первое неравенство в системе (
обратите внимание, на то что по условию корней может быть два или один. Поэтому первое неравенство в системе ( 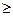 ).
).
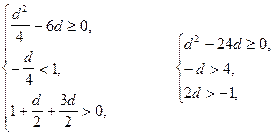
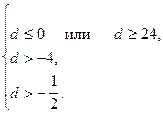 откуда
откуда
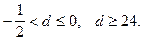
Задача6. При каких значениях параметра а число 2 находится между корнями квадратного уравнения 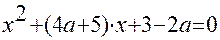 .
.
Решение.
В предыдущих задачах поиск корней квадратной функции был связан с нахождением дискриминанта.
Поступим также и в этой задаче.
Имеем 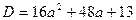
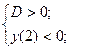
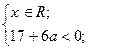
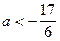 .
.
Ответ: 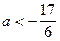 .
.
