П.6.2. Взаимное расположение двух прямых

Рассмотрим две прямые, заданные уравнениями в общем виде:

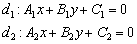
Две прямые могут:

1) совпадать;

2) быть параллельными: ;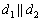

3) пересекаться в единственной точке: .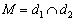

Как определить взаимное расположение двух прямых?

Теорема 1. две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства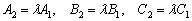

Пример 10.

Рассмотрим прямые 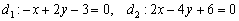и составим три уравнения из соответствующих коэффициентов: 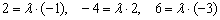. Из каждого уравнения следует, что 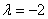, следовательно, данные прямые совпадают.

Второй случай, когда прямые параллельны:

Теорема 2. Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных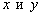 пропорциональны: 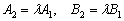, но .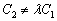

Пример 11.

В качестве примера рассмотрим две прямые 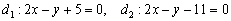. Проверяем пропорциональность соответствующих коэффициентов при переменных :

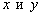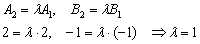
Однако совершенно очевидно, что .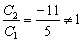

Вывод: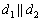

И третий случай, когда прямые пересекаются:

Теорема 3. Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных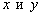 НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства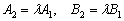

Так, для прямых 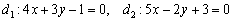составим систему:

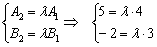
Из первого уравнения следует, что 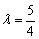, а из второго уравнения: 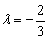, значит, система несовместна (решений нет). Таким образом, коэффициенты при переменных 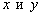не пропорциональны.

Вывод: прямые пересекаются

Пример 12.

Выяснить взаимное расположение прямых:

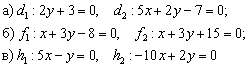
Решение основано на исследовании направляющих векторов прямых:

а) Из уравнений 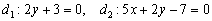найдём направляющие векторы прямых: .

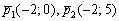Вычислим определитель, составленный из координат данных векторов:
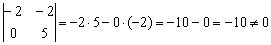, значит, векторы 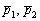не коллинеарны и прямые 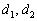пересекаются.

б) Найдем направляющие векторы прямых :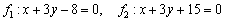

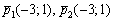
Прямые имеют один и тот же направляющий вектор, значит, они либо параллельны, либо совпадают. Тут и определитель считать не надо.

Очевидно, что коэффициенты при неизвестных 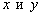пропорциональны, при этом .

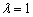Выясним, справедливо ли равенство :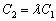

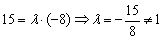
Таким образом,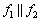

в) Найдем направляющие векторы прямых :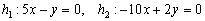

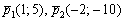
Вычислим определитель, составленный из координат данных векторов:
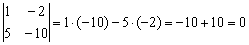, следовательно, направляющие векторы коллинеарны. Прямые либо параллельны либо совпадают.

Коэффициент пропорциональности «лямбда» можно узнать прямо соотношения коллинеарных направляющих векторов 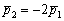. Впрочем, можно и через коэффициенты самих уравнений: .

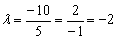Теперь выясним, справедливо ли равенство 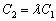. Оба свободных члена нулевые, поэтому:

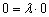
Полученное значение 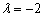удовлетворяет данному уравнению (ему удовлетворяет вообще любое число).

Таким образом, прямые совпадают.

Ответ: 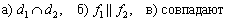.