Признак существования предела функции
Не всякая функция имеет предел, даже будучи ограниченной. Например, 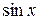 при
при 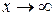 предела не имеет, хотя
предела не имеет, хотя 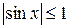 .
.
При решении некоторых задач бывает достаточно только убедиться в существовании предела функции, а числовое значение предела при этом имеет второстепенную роль. В таких случаях пользуются признаками существования предела.
Укажем такой признак.
Теорема.
Если функция 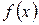 заключена между двумя функциями
заключена между двумя функциями 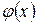 и
и 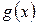 , стремящимися к одному и тому же пределу, то она также стремится к этому пределу, т.е. если
, стремящимися к одному и тому же пределу, то она также стремится к этому пределу, т.е. если
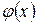
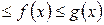 ,
, 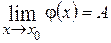 ,
, 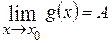 ,
,
то
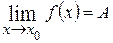 .
.
Два замечательных предела
Замечательными (вследствие большого числа их приложений) в математике называются пределы двух следующих функций, когда их аргумент х стремится к нулю:
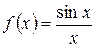 и
и 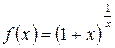 .
.
Первый замечательный предел
Теорема.
Предел отношения синуса бесконечно малого угла к величине этого угла в радианах равен единице:
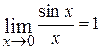 .
.
Это равенство указывает на тот факт, что при очень «небольших» значениях х
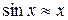 .
.
Первый замечательный предел часто используют при вычислении пределов выражений, содержащих тригонометрические функции.
Второй замечательный предел
Можно доказать, что функция
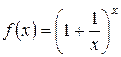
при 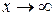 стремится к числу е:
стремится к числу е:
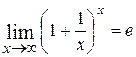 .
.
Число е иррациональное, его приближенное значение равно 2,72 ( 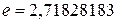 …). Число е служит основанием натуральных логарифмов (
…). Число е служит основанием натуральных логарифмов ( 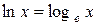 ) и играет важную роль в математике.
) и играет важную роль в математике.
Дадим другое выражение для числа е. Полагая 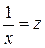 (
( 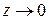 , т.к.
, т.к. 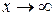 ), будем иметь
), будем иметь
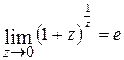 .
.
Оба равенства называют вторым замечательным пределом. С помощью числа е удобно выражать многие пределы.
Замечание.
Показательная функция вида
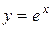
называется экспоненциальной, употребляется также обозначение
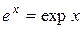 .
.
Эквивалентные бесконечно малые
Пусть 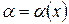 и
и 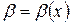 − бесконечно малые функции при
− бесконечно малые функции при 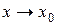 (или
(или 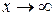 ), т.е.
), т.е. 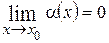 и
и 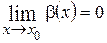 .
.
Если 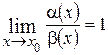 , то
, то 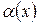 и
и 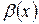 называются эквивалентными бесконечно малыми (при
называются эквивалентными бесконечно малыми (при 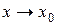 ).
).
Обозначается: 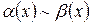 .
.
Например, 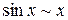 при
при 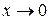 , т.к.
, т.к. 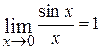 .
.
Для эквивалентных бесконечно малых справедливы следующие свойства:
1. Если 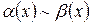 при
при 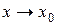 , то
, то 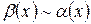 .
.
2. Если 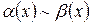 и
и 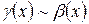 при
при 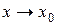 , то
, то 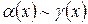 при
при 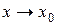 .
.
3. Если 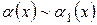 и
и 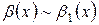 при
при 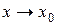 , то
, то 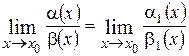 , т.е. предел отношения двух бесконечно малых величин равен пределу отношения эквивалентных им бесконечно малых.
, т.е. предел отношения двух бесконечно малых величин равен пределу отношения эквивалентных им бесконечно малых.
Последнее свойство означает, что при нахождении предела, можно бесконечно малые, стоящие в числителе или в знаменателе или в обоих, заменять эквивалентными им величинами, в частности, более простыми. Такой прием часто применяют при вычислении пределов функций.
Ниже приведены важнейшие эквивалентности, которыми пользуются при вычислении пределов функций:
| 1. |  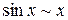 | при 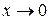 |
| 2. | 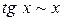 | |
| 3. | 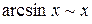 | |
| 4. | 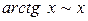 | |
| 5. | 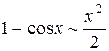 | |
| 6. | 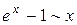 | |
| 7. | 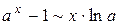 | |
| 8. | 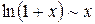 | |
| 9. | 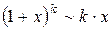 |
