Параллельный перенос системы координат

Пусть на плоскости заданы две декартовы прямоугольные системы координат: 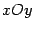("старая") и 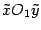("новая"), причем как оси абсцисс, так и оси ординат обеих систем параллельны и одинаково направлены (рис. 12.19)

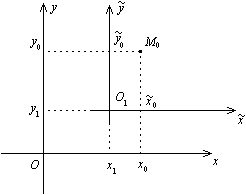
Рис.12.19.Параллельный перенос системы координат

В этом случае говорят, что одна система координат получается из другой "параллельным переносом".

Пусть начало 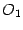"новой" системы координат имеет в "старой" системе координат координаты 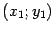, и пусть 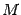-- некоторая точка плоскости. Обозначим координаты точки 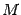в "старой" системе координат 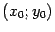, а в "новой" -- 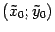. Из рис. 12.19 ясно, что 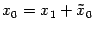, 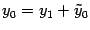. Откуда 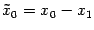, 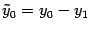. Так как точка 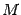взята произвольно, то индекс 0 в записи ее координат, как "старых", так и "новых", можно убрать. Получаем связь между "старыми" и "новыми" координатами точки при параллельном переносе осей координат:

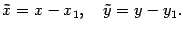(12.11)

Выясним теперь, как связаны друг с другом уравнения одной и той же кривой в "старых" и "новых" координатах.

Пусть некоторая кривая задана уравнением 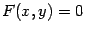. Тогда в системе координат 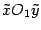, полученной параллельным переносом, с началом в точке 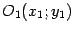уравнение кривой будет иметь вид .

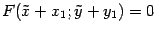Однако, для практического использования это предложение удобнее сформулировать немного подругому.

Пусть некоторая кривая задана уравнением 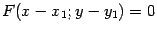. Тогда в системе координат 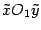, полученной параллельным переносом, с началом в точке 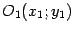уравнение кривой будет иметь вид .

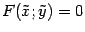Доказательство обоих предложений очевидным образом следует из формул (12.11) связи между старыми и новыми координатами.

ПримерНарисуйте кривую 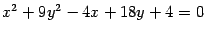и найдите ее фокусы.

Решение. Выделим полные квадраты по переменным 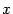и 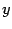(см. пример 12.1):

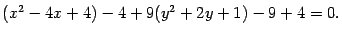
Откуда

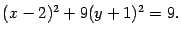
Разделим обе части на 9:

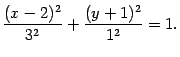
Введем новую систему координат с началом в точке 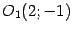, получающуюся из старой параллельным переносом. По предложению 12.7 получим, что кривая задается уравнением

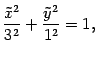
а это -- каноническое уравнение эллипса с полуосями 3 и 1. Сделаем рисунок (рис. 12.20).

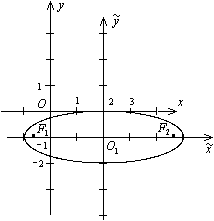
Рис.12.20.Эллипс, заданный уравнением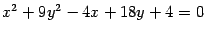

Из формулы (12.5) 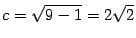. Поэтому фокусы в новой системе координат имеют координаты 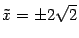, 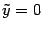. Используя формулы (12.11), находим старые координаты фокусов 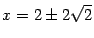, 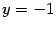. Таким образом, фокусами являются точки , .

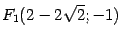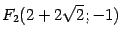ПримерПостройте параболу

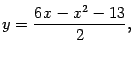
найдите ее фокус и директрису.

Решение. Преобразуем уравнение к виду 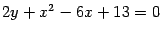и выделим полный квадрат по переменному :

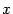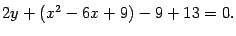
Из этого уравнения получим 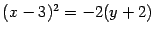. Произведем параллельный перенос осей координат: 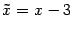, , 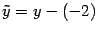новое начало координат -- 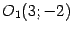. В новых координатах уравнение параболы примет вид 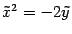, которое тоже не является каноническим. Но если мы изменим направление оси ординат и переобозначим оси: 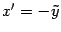, , 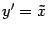то получим уравнение 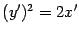. Это уравнение -- каноническое, 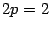, 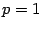. Строим оси и параболу (рис. 12.21).

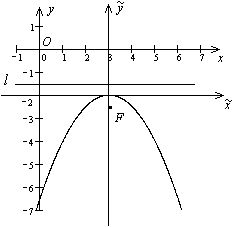
Рис.12.21.Парабола, заданная уравнением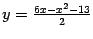

В системе координат 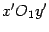фокус имеет координаты 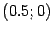, а директриса задается уравнением 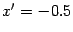. В системе координат 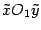координаты фокуса -- 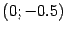, а уравнение директрисы 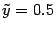. Наконец, в исходной системе координат 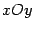получим фокус 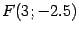и уравнение директрисы 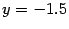, что и служит ответом к задаче.

Пример 12.9 Постройте кривую

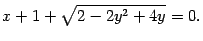
Решение. Преобразуем уравнение к виду

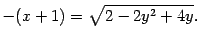(12.12)

Возведем обе части в квадрат:

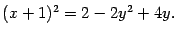
При этом появились новые точки, которые удовлетворяют последнему уравнению, но не удовлетворяют уравнению (12.12). Эти посторонние точки мы отбросим потом. Выделим полный квадрат по переменному :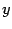

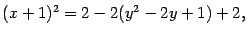
то есть

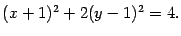
Обе части разделим на 4 и произведем параллельный перенос системы координат: 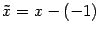, 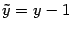. Получим уравнение

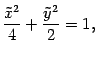
которое является каноническим уравнением эллипса с полуосями: 2 и 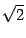. Нарисуем его (рис. 12.22).

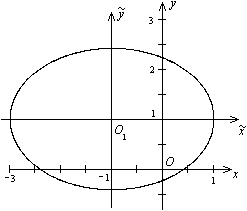
Рис.12.22.Эллипс, заданный уравнением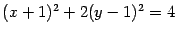

Чтобы отбросить посторонние точки, возникшие при возведении в квадрат, преобразуем уравнение (12.12) к виду

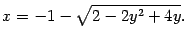
Из этого уравнения видно, что 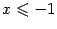. Поэтому от нарисованного ранее эллипса нужно оставить только левую половину (рис. 12.23).

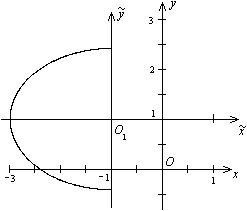
Рис.12.23.Кривая, заданная уравнением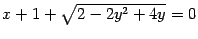

Литература

1. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.

2. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.

3. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: "Наука", 1988.