Бесконечно малые величины и их свойства
Единственность предела и ограниченность сходящейся числовой последовательности
Определение 1. Числовая последовательность 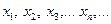 (1) называется ограниченной, если множество членов этой последовательности образует ограниченное множество.
(1) называется ограниченной, если множество членов этой последовательности образует ограниченное множество.
В этом случае числовую последовательность (1) мы будем называть ограниченной величиной.
Определение 2. Числовая последовательность (1) сходится и имеет предел 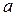 (Возможно использование записи
(Возможно использование записи 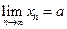 ), если
), если 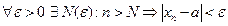 .
.
Давайте повторим это определение, используя в большей степени русский язык. Предел числовой последовательности существует и равен некоторому числу, если, начиная с некоторого номера, все члены последовательности удалены от этого предельного числа менее, чем любое, наперед заданное, сколь угодно малое положительное число. Можно это же самое сказать другими словами. Число 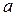 будет пределом числовой последовательности (1) тогда и только тогда, когда для каждой
будет пределом числовой последовательности (1) тогда и только тогда, когда для каждой 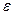 -окрестности точки
-окрестности точки 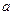 все члены последовательности, начиная с некоторого номера, лежат в этой
все члены последовательности, начиная с некоторого номера, лежат в этой 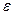 –окрестности. Заметим, что интервал
–окрестности. Заметим, что интервал 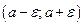 называется
называется  -окрестностью точки
-окрестностью точки  .
.
Теорема 1. Если предел числовой последовательности существует, то он единственный.
Доказательство. Доказательство теоремы проведем «методом от противного». Предположим, что теорема неверна и существует, как минимум, 2 числа 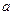 и
и 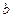 (
( 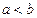 ), для которых выполнены условия определения 2. В этом определении возьмем
), для которых выполнены условия определения 2. В этом определении возьмем 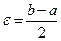 . Тогда, после номера
. Тогда, после номера  члены последовательности отличаются от числа
члены последовательности отличаются от числа 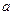 меньше чем на
меньше чем на 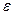 , а после номера
, а после номера 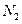 члены последовательности отличаются от числа
члены последовательности отличаются от числа 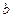 меньше чем на
меньше чем на 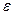 . Покажем, что этого не может быть. В самом деле, при
. Покажем, что этого не может быть. В самом деле, при 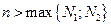 выполнены соотношения
выполнены соотношения 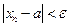 ,
, 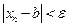 , откуда для этих
, откуда для этих 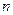 имеем
имеем 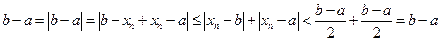 . Теорема доказана.
. Теорема доказана.
Теорема 2. Если числовая последовательность имеет предел, то эта числовая последовательность ограничена.
Доказательство. Доказательство будет носить конструктивный характер. Возьмем 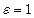 и найдем соответствующее
и найдем соответствующее 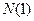 . Разобьем последовательность на 2 части: первые
. Разобьем последовательность на 2 части: первые 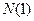 членов и остальные члены последовательности. Первая группа состоит из конечного числа членов и поэтому ограничена. Вторая группа состоит из чисел, удаленных от предельного значения
членов и остальные члены последовательности. Первая группа состоит из конечного числа членов и поэтому ограничена. Вторая группа состоит из чисел, удаленных от предельного значения 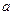 не больше чем на 1, и поэтому также ограничена. Объединение двух ограниченных множеств есть множество ограниченное. Теорема доказана.
не больше чем на 1, и поэтому также ограничена. Объединение двух ограниченных множеств есть множество ограниченное. Теорема доказана.
Бесконечно малые величины и их свойства
Определение 3. Числовая последовательность называется бесконечно малой величиной, если она имеет предел, равный 0.
Для бесконечно малых величин используются обозначение б. м.
Пусть заданы числовые последовательности 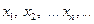 и
и 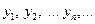 . Числовая последовательность с общим членом
. Числовая последовательность с общим членом 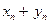 ,
, 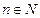 называется суммой этих числовых последовательностей. Числовая последовательность с общим членом
называется суммой этих числовых последовательностей. Числовая последовательность с общим членом 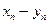 ,
, 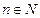 называется суммой этих числовых последовательностей. Числовая последовательность с общим членом
называется суммой этих числовых последовательностей. Числовая последовательность с общим членом 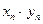 ,
, 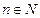 называется суммой этих числовых последовательностей.
называется суммой этих числовых последовательностей.
Теорема 3. Сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
Доказательство. Достаточно доказать утверждение для суммы двух б. м. Пусть числовые последовательности 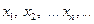 и
и 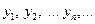 являются бесконечно малыми величинами, т. е. пределы этих последовательностей равны 0. Данный факт означает следующее. Если задано произвольное, скроль угодно малое положительное число
являются бесконечно малыми величинами, т. е. пределы этих последовательностей равны 0. Данный факт означает следующее. Если задано произвольное, скроль угодно малое положительное число 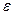 , то для числа
, то для числа 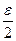 и числовой последовательности
и числовой последовательности 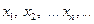 существует номер
существует номер 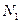 , обладающий тем свойством, что при
, обладающий тем свойством, что при 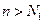 выполнено соотношение
выполнено соотношение 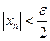 . По той же причине для этого же числа
. По той же причине для этого же числа 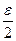 и числовой последовательности
и числовой последовательности 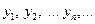 существует номер
существует номер 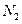 , обладающий тем свойством, что при
, обладающий тем свойством, что при 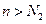 выполнено соотношение
выполнено соотношение 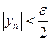 . Возьмем число
. Возьмем число 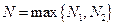 , тогда при
, тогда при 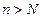 справедливы соотношения
справедливы соотношения 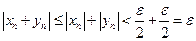 . Итак, для произвольного
. Итак, для произвольного 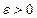 мы нашли номер
мы нашли номер 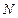 , такой что при
, такой что при 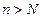 выполнено
выполнено 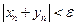 . Следовательно, предел последовательности
. Следовательно, предел последовательности 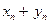 ,
, 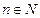 равен 0, и она является бесконечно малой величиной. Теорема доказана.
равен 0, и она является бесконечно малой величиной. Теорема доказана.
Теорема 4. Произведение бесконечно малой величины на ограниченную величину есть величина бесконечно малая.
Доказательство. Пусть числовая последовательность 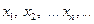 является бесконечно малой величиной, а числовая последовательность
является бесконечно малой величиной, а числовая последовательность 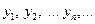 является ограниченной величиной. Это означает что, с одной стороны,
является ограниченной величиной. Это означает что, с одной стороны, 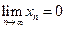 , с другой стороны, существует число
, с другой стороны, существует число 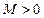 такое, что для каждого
такое, что для каждого 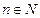 выполнено условие
выполнено условие 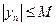 . Пусть теперь задано произвольное, скроль угодно малое положительное число
. Пусть теперь задано произвольное, скроль угодно малое положительное число 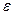 . Рассмотрим числа
. Рассмотрим числа 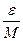 , для него в числовой последовательности
, для него в числовой последовательности 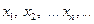 существует номер
существует номер 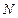 , обладающий тем свойством, что при
, обладающий тем свойством, что при 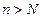 выполнено соотношение
выполнено соотношение 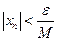 . При этом будет выполнено условие
. При этом будет выполнено условие 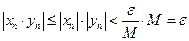 , что и означает, что произведение этих двух величин – бесконечно малой и ограниченной есть величина бесконечно малая. Теорема доказана.
, что и означает, что произведение этих двух величин – бесконечно малой и ограниченной есть величина бесконечно малая. Теорема доказана.
Свойства пределов
А как конкретно происходит вычисление пределов, в данном случае числовых последовательностей? Мы стараемся представить величину, предел которой надо найти, в виде суммы, разности, произведения, частного более простых величин, предел которых легко найти. Для обоснования такого подхода надо сформулировать и доказать свойства пределов.
Теорема 5. Числовая последовательность 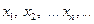 имеет предел, равный
имеет предел, равный 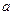 тогда и только тогда, когда последовательность
тогда и только тогда, когда последовательность 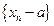 ,
, 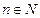 является бесконечно малой величиной.
является бесконечно малой величиной.
Доказательство. Пусть 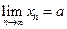 , т.е. при для каждого
, т.е. при для каждого 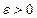 при
при 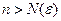 выполнено неравенство
выполнено неравенство 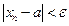 (
( 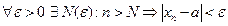 ). Но это неравенство равносильно тому, что
). Но это неравенство равносильно тому, что 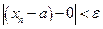 , т. е. последовательность
, т. е. последовательность 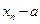 ,
, 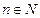 имеет предел 0, т.е. является бесконечно малой величиной. Теорема доказана.
имеет предел 0, т.е. является бесконечно малой величиной. Теорема доказана.
Теорема 6. (Свойства пределов) Пусть 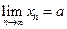 ,
, 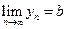 , тогда
, тогда 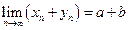 ,
, 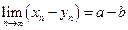 ,
, 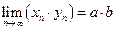 , а если, кроме того,
, а если, кроме того, 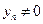 ,
, 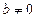 , то
, то 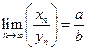 .
.
Доказательство. Докажем в условиях теоремы формулу 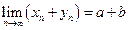 , т. е. мы докажем, что предел суммы последовательностей равен сумме их пределов, если каждый из пределов существует. Так как
, т. е. мы докажем, что предел суммы последовательностей равен сумме их пределов, если каждый из пределов существует. Так как 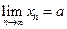 , то
, то 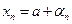 , где
, где 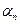 - б. м. Аналогично
- б. м. Аналогично 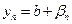 , где
, где 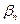 - б. м. Отсюда следует, что
- б. м. Отсюда следует, что 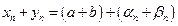 . В последней скобке сумма двух бесконечно малых величин есть величина б. м. Поэтому
. В последней скобке сумма двух бесконечно малых величин есть величина б. м. Поэтому 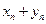 представляется в виде суммы
представляется в виде суммы 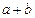 и бесконечно малой величины
и бесконечно малой величины 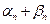 . В силу теоремы 5 это означает, что
. В силу теоремы 5 это означает, что 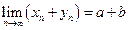 . Первое утверждение теоремы доказана. Формула
. Первое утверждение теоремы доказана. Формула 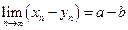 доказывается совершенно аналогично. Рассмотрим теперь формулу
доказывается совершенно аналогично. Рассмотрим теперь формулу 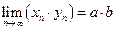 и используем для преобразования левой части те же обозначения. Поэтому
и используем для преобразования левой части те же обозначения. Поэтому 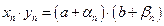 …
…
