Классификация особых точек ФКП. Изолированные особые точки
Точка а 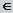 Сz называется изолированной особой точкой однозначного характера функции f (z), если f (z) аналитическая и однозначная (регулярная) в кольце {z:0<|z–a|< }, а в самой точке а не определена.
Сz называется изолированной особой точкой однозначного характера функции f (z), если f (z) аналитическая и однозначная (регулярная) в кольце {z:0<|z–a|< }, а в самой точке а не определена.
Бесконечно удаленная точка называется изолированной особой точкой однозначного характера функции f (z), если f (z) регулярна в некоторой окрестности {R<|z|< 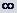 } точки z=
} точки z= 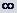 и функция
и функция 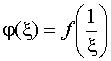
имеет в точке =0 изолированную особую точку однозначного характера.
В зависимости от поведения функции f (z) вблизи точки а различают следующие три типа особых точек.
Изолированная особая точка а функции f (z) называется
а) устранимой особой точкой, если существует конечный предел
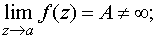
б) полюсом, если
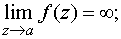
в) существенно особой точкой, если
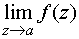
не существует.
Вычеты, их вычисление в особых точках. Вычет в бесконечно удаленной точке.
Вычет относительно бесконечно удаленной точки
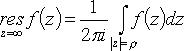
(f(z) - аналитическая в области 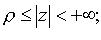 обход контура - по часовой стрелке).
обход контура - по часовой стрелке).
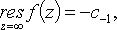
c-1 - коэффициент при z-1 в разложении f(z) в ряд Лорана в окрестности точки 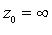 .
.
Вычисление вычета в бесконечно удаленной точке
1. 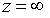 - правильная точка:
- правильная точка:
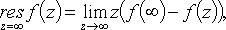
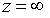 - нуль:
- нуль: 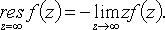
В частности, если 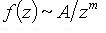 при
при 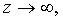 то
то
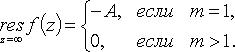
2. 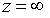 - полюс порядка не выше m:
- полюс порядка не выше m:
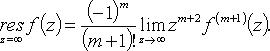
3. Если f(z) представима в виде 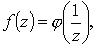 где
где 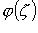 - аналитическая в точке
- аналитическая в точке 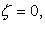 то
то 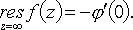
Если f(z) имеет конечное число особых точек zk, k = 1, 2, ..., n, в конечной части плоскости, то 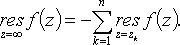
Основная теорема о вычетах. Теорема о сумме всех вычетов.
Если 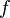 аналитична в некоторой замкнутой односвязной области
аналитична в некоторой замкнутой односвязной области 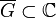 , за вычетом конечного числа особых точек
, за вычетом конечного числа особых точек 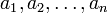 , из которых ни одна не принадлежит граничному контуру
, из которых ни одна не принадлежит граничному контуру 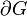 , то справедлива следующая формула:
, то справедлива следующая формула:
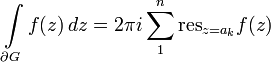 , где
, где 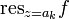 — вычет
— вычет 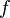 в точке
в точке 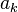 .
.
Из теоремы о В. вытекает теорема о полной сумме вычетов: если f(z) - однозначная аналитич. функция в расширенной комплексной плоскости, кроме конечного числа особых точек, то сумма всех В. функции f(z), включая В. в бесконечно удаленной точке, равна нулю.
38. Вычисления определенных интегралов по отрезку [0,2п] от рациональной функции относительно sint и cost и несобственных интегралов с бесконечными пределами рациональных функций.
Рассмотрим интеграл вида
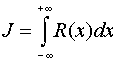 ,
,
где R(x) – рациональная функция, 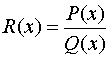 , причем многочлен Q(x) не обращается в нуль на вещественной оси и его степень по крайней мере на две единицы больше степени числителя. В этом случае интеграл сходится и его значение определяется по формуле
, причем многочлен Q(x) не обращается в нуль на вещественной оси и его степень по крайней мере на две единицы больше степени числителя. В этом случае интеграл сходится и его значение определяется по формуле
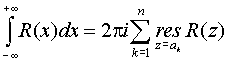 ,
,
Вычисления определённых интегралов от тригонометрических функций
Пусть функция 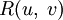 — рациональная функция переменных
— рациональная функция переменных 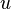 и
и 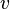 . Для вычисления интегралов вида
. Для вычисления интегралов вида 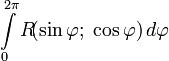 удобно использовать формулы Эйлера. Положив, что
удобно использовать формулы Эйлера. Положив, что 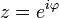 , и произведя соответствующие преобразования, получим:
, и произведя соответствующие преобразования, получим:
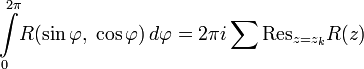 .
.
