Квадратные уравнения с параметрами
Рассмотрим теперь квадратное уравнение
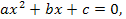 (1)
(1)
где 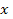 - неизвестная величина,
- неизвестная величина, 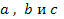 - параметры (коэффициенты) уравнения.
- параметры (коэффициенты) уравнения.
К критическим значениям параметра 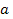 следует отнести, прежде всего, значение
следует отнести, прежде всего, значение 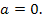 При указанном значении параметра уравнение (1) принимает вид
При указанном значении параметра уравнение (1) принимает вид
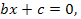 (2)
(2)
следовательно, порядок уравнения понижается на единицу. Уравнение (2) является линейным уравнением и метод его решения рассматривался ранее.
При 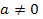 другие критические значения параметров
другие критические значения параметров 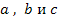 определяются дискриминантом
определяются дискриминантом 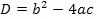 уравнения. Известно, что при
уравнения. Известно, что при 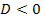 уравнение (1) корней не имеет; при
уравнение (1) корней не имеет; при 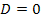 оно имеет единственный корень
оно имеет единственный корень 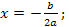 при
при 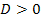 уравнение (1) имеет два различных корня
уравнение (1) имеет два различных корня 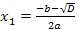 и
и 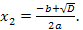
1). Найти все значения параметра 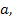 для которых квадратное уравнение
для которых квадратное уравнение 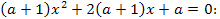
а) имеет два различных корня;
б) не имеет корней;
в) имеет два равных корня.
Решение. Данное уравнение по условию является квадратным, а поэтому 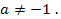 Рассмотрим дискриминант данного уравнения
Рассмотрим дискриминант данного уравнения
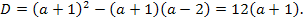
При 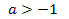 уравнение имеет два различных корня, т.к.
уравнение имеет два различных корня, т.к. 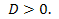
При 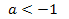 уравнение корней не имеет, т.к.
уравнение корней не имеет, т.к. 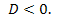 Данное квадратное уравнение не может иметь двух равных корней, т.к.
Данное квадратное уравнение не может иметь двух равных корней, т.к. 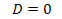 при
при 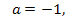 а это противоречит условию задачи.
а это противоречит условию задачи.
Ответ: При 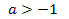 уравнение имеет два различных корня.
уравнение имеет два различных корня.
При 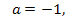
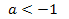 уравнение корней не имеет.
уравнение корней не имеет.
2).Решить уравнение . Для каждого допустимого значения параметра 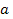 решить уравнение
решить уравнение 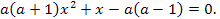
Решение. Рассмотрим сначала случай, когда
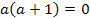 ⟺
⟺ 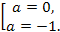
(в этом случае исходное уравнение становится линейным уравнением). Таким образом, значение параметра 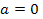 и
и 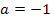 являются его критическими значениями. Ясно, что при
являются его критическими значениями. Ясно, что при 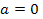 корнем данного уравнения является
корнем данного уравнения является 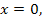 а при
а при 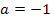 его корнем является
его корнем является 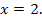
Если 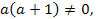 т.е.
т.е. 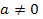 и
и 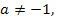 то данное уравнение является квадратным. Найдем его дискриминант:
то данное уравнение является квадратным. Найдем его дискриминант:
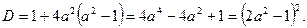
При всех значениях 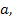 дискриминант принимает неотрицательные значения, причем он обращается в нуль при
дискриминант принимает неотрицательные значения, причем он обращается в нуль при 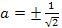 (эти значения параметра тоже являются его критическими значениями).
(эти значения параметра тоже являются его критическими значениями).
Поэтому, если 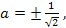 то данное уравнение имеет единственный корень
то данное уравнение имеет единственный корень
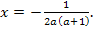 При этом значению параметра
При этом значению параметра 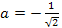 соответствует корень
соответствует корень
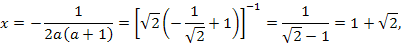
а значению 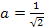 соответствует корень
соответствует корень
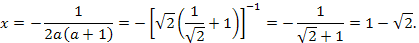
Если же 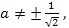
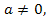
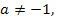 то уравнение имеет два различных корня. Найдем эти корни.
то уравнение имеет два различных корня. Найдем эти корни.
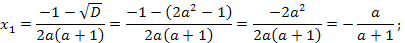
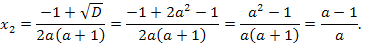
Ответ. Если 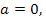 то
то 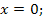 если
если 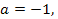 то
то 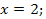 если
если 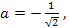 то
то 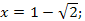
если 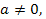
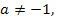
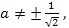 то
то 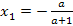 ,
, 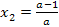 .
.
3).Решить уравнение. При каких значениях параметра а уравнение 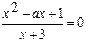 имеет единственное решение?
имеет единственное решение?
Решение. Данное уравнение равносильно системе
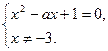
Наличие квадратного уравнения и условие единственности решения, естественно, приведут к поиску корней дискриминанта. Вместе с тем условие х ≠ -3 должно привлечь внимание. И «тонкий момент» заключается в том, что квадратное уравнение системы может иметь два корня! Но обязательно только один из них должен равняться -3. Имеем
D = а2 - 4 , отсюда D =0, если а = ±2; х = -3 — корень уравнения х2 – ах +1 = 0 при
а = -10/3, причем при таком значении а второй корень квадратного уравнения отличен
от -3.
Ответ . а = ±2 или а = -10/3.
4).Решить уравнение. При каких значениях параметра а уравнение
(а - 2)x2 + (4 - 2а) х +3 = 0 имеет единственное решение?
Решение. Понятно, что надо начинать со случая а = 2. Но при а = 2 исходное уравнение вообще не имеет решений. Если а ≠ 2, то данное уравнение — квадратное, и, казалось бы, искомые значения параметра — это корни дискриминанта. Однако дискриминант обращается в нуль при а = 2 или а = 5. Поскольку мы установили, что а= 2 не подходит, то
Ответ, а = 5.
9).Решить уравнение. При каких значениях параметра а уравнение ах2 - 4х + а + 3 = 0 имеет более одного корня?
Решение. При а = 0 уравнение имеет единственный корень, что не удовлетворяет условию. При а ≠ 0 исходное уравнение, будучи квадратным, имеет два корня, если его дискриминант 16 – 4а2 – 12а положительный. Отсюда получаем -4 <а<1.
Однако в полученный промежуток (-4; 1) входит число 0.Ответ. -4<а<0 или 0<а<1.
10). При каких значениях параметра а уравнение а(а +3)х2 + (2а +6)х – 3а – 9 = 0 имеет более одного корня?
Решение. Стандартный шаг — начать со случаев а = 0 и а = -3. При а = 0 уравнение имеет единственное решение. Любопытно, что при а = -3 решением уравнения служит любое действительное число. При а ≠ -3 и а ≠ 0, разделив обе части данного уравнения на а + 3, получим квадратное уравнение ах2 + 2х - 3 = 0, дискриминант которого 4 (1 + За) положителен при а > ⅓. Опыт предыдущих примеров подсказывает, что из промежутка
(-⅓ ;∞) надо исключить точку а = 0, а в ответ не забыть включить а = -3.
Ответ. а = -3, или - ⅓ < а < 0, или а > 0.
11).Решить уравнение : 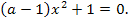
Решение. Сначала заметим, что при 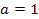 данное уравнение равносильно уравнению
данное уравнение равносильно уравнению 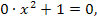 которое не имеет решений. Если же
которое не имеет решений. Если же 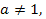 то можно записать
то можно записать
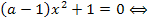
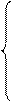 | 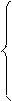 |
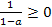 ,
, 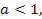
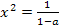 ⟺ ⟺
⟺ ⟺
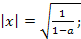
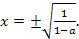
Ответ. Если 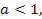 то
то 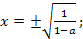 если
если 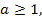 то
то 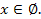
. Задачи на расположение корней квадратного трехчлена в зависимости от параметра могут быть разнообразные: найти значение параметра, при котором корни положительны, отрицательны, имеют разный знак, больше или меньше какого-либо числа, принадлежат данному отрезку или когда отрезок находится между корнями трехчлена.
