Определители второго и третьего порядков

Любая квадратная матрица А имеет свой определитель. Прямоугольная, неквадратная матрица определителя не имеет.

Определение. Определителем (или детерминантом) второго порядка, соответствующим матрице

,

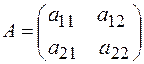называется число, обозначаемое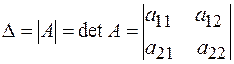

и вычисляется по правилу 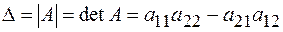. Т.е. определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов дополнительной диагонали.

Определение. Определителем (или детерминантом) третьего порядка, соответствующим матрице

,

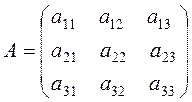называется число, обозначаемое

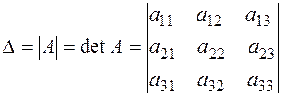
и вычисляемое по правилу Саррюса

.

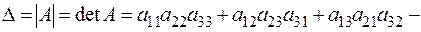
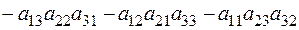Для того чтобы запомнить формулу вычисления определителя третьего порядка проиллюстрируем правило Саррюса, которое символически можно записать так

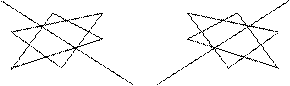
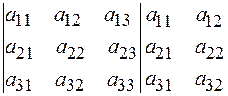или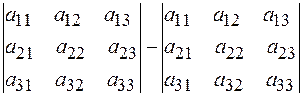

Определение. Минором М_ij элемента а_ij (i-номер строки, j-номер столбца) данного определителя называется определитель, полученный из данного путем вычеркивания i-строки и j-столбца.

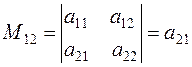– минор элемента а₁₂ определителя второго порядка;

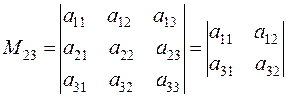– минор элемента а₂₃ определителя третьего порядка.

Определение. Алгебраическим дополнением элемента а_ij данного определителя называется число А_ij=(– 1)^i+j∙M_ij, где M_ij – минор элемента а_ij.

Например, А₁₂ = − а₂₁ – алгебраическое дополнение элемента а₁₂ определителя второго порядка.

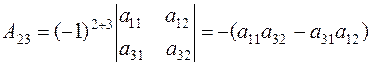– алгебраическое дополнение элемента а₂₃ определителя третьего порядка.

1.3.Свойства определителей

С в о й с т в о 1. (о разложении определителя по элементам строки или столбца). Определитель равен сумме произведений элементов любой строки (или любого столбца) на их алгебраические дополнения.

Например, разложим определитель третьего порядка по элементам первой строки:

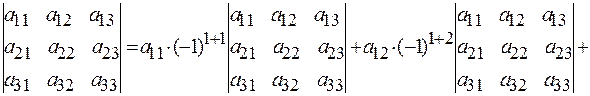
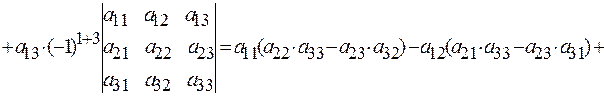
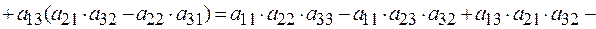
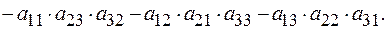
Сравнивая с результатом применения правила Саррюса видим их полное совпадение.

С в о й с т в о 2. При транспонировании матрицы ее определитель не меняется, т. е.

det A = det A^T.

С в о й с т в о 3. Общий множитель элементов какого-либо столбца или какой-либо строки можно вынести за знак определителя:

.

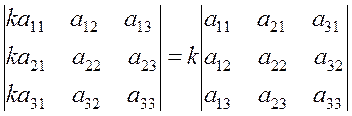Другими словами, если определитель умножается на число, то умножаются на это число все элементы какой-нибудь строки или какого-нибудь столбца.

С в о й с т в о 4. Определитель, у которого все элементы какой-нибудь строки или какого-нибудь столбца равны нулю, равен нулю.

С в о й с т в о 5. Если в определителе поменять местами две любые строки (столбца), то знак определителя изменится.

С в о й с т в о 6. Если в определителе элементы какой-либо строки (столбца) равны или пропорциональны соответствующим элементам другой строки (столбца), то он равен нулю.

С в о й с т в о 7. Если в определителе элементы какой-нибудь строки (столбца) представляют собой суммы двух слагаемых, то он может быть разложен на сумму двух соответствующих определителей, например:

.

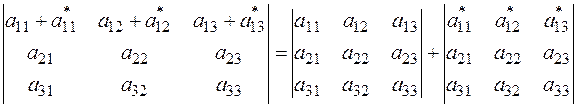С в о й с т в о 8. Если к элементам некоторого строки (столбца) прибавить соответствующие элементы другого строки (столбца), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,

.

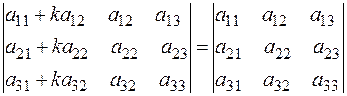С в о й с т в о 9. Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения другой строки (столбца) равна нулю. Например,

а₁₁ ∙А₁₂ + а₂₁ ∙А₂₂ + а₃₁ ∙А₃₂ = 0.

С в о й с т в о 10. Определитель произведения квадратных матриц равен произведению определителей этих матриц, т. е. если А и В квадратные матрицы одного порядка, то |A∙B| = |A|∙|B|.

Аналогично можно ввести понятия определителей четвертого, пятого,…, n-порядков, их миноры и алгебраические дополнения и показать, что они обладают рассмотренными выше свойствами.

1.4. Сводная таблица основных методов решения определителей