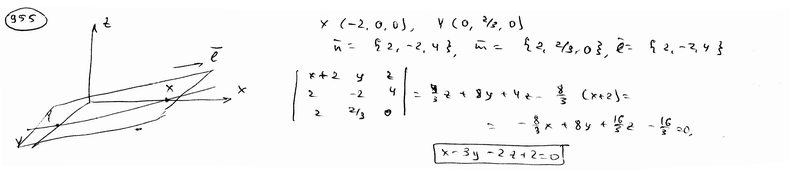| | | Составить уравнение плоскости, которая проходит через точку М1(2; 1; -1) и имеет нормальный вектор n={1; -2; 3}. 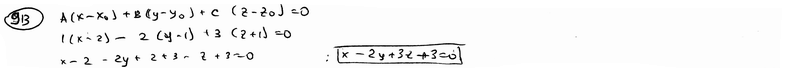 |
| | | Составить уравнение плоскости, которая проходит через начало координат и имеет нормальный вектор n={5; 0; -3}. |
| | |  |
| | | Точка Р(2; -1; -1) служит основанием перпендикуляра, опущенного из начала координат на плоскость. Составить уравнение этой плоскости. 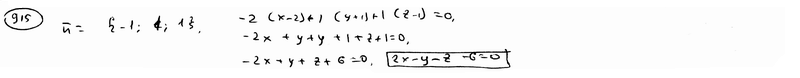 |
| | | Даны точки M1(3; -1; 2), M2(4; -2; -1). Составить уравнение плоскости, проходящей через точку М1 перпендикулярно вектору 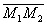 . . 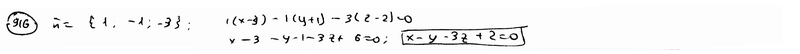 |
| | | Составить уравнение плоскости, проходящей через точку М1(3; 4; -5) параллельно векторам a1={3; 1; -1) и a2={1; -2; 1}. 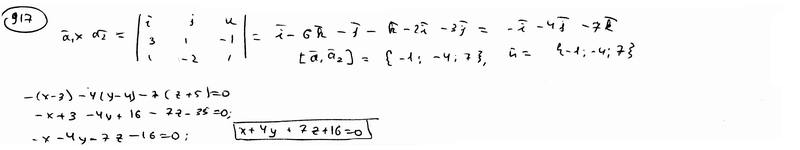 |
| | | Доказать, что уравнение плоскости, проходящей через точку М0(x0, y0, z0) параллельно векторам a1={l1, m1, n1} и a2={l2; m2; n2}, может быть представлено в следующем виде: 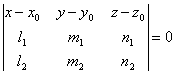 . .  |
| | | Составить уравнение плоскости, проходящей через точки M1(2; -1; 3), M2(3; 1; 2) параллельно вектору a={3; -1; 4}. 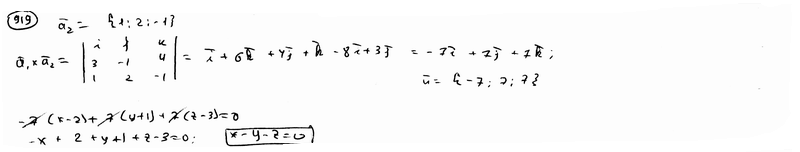 |
| | | Доказать, что уравнение плоскости, проходящей через точки M1(x1; y1; z1), M2(x2, y2, z2) параллельно вектору a={l; m; n}, может быть представлено в следующем виде: 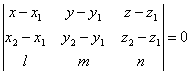 . . 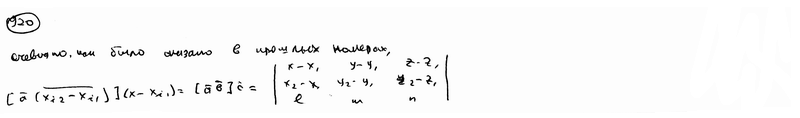 |
| | | Составить уравнение плоскости, проходящей через точки М1(3; -1; 2), М2(4; -1; -1), М3(2; 0; 2).  |
| | | Доказать, что уравнение плоскости, проходящей через точки M1(x1; y1; z1), M2(x2, y2, z2), M3(x3; y3; z3), может быть представлено в следующем виде: 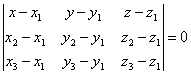 . . 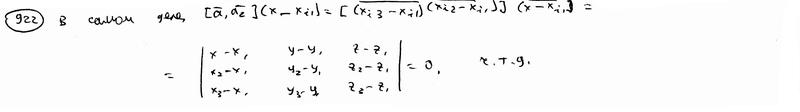 |
| | | Определить координаты какого-нибудь нормального вектора каждой из следующих плоскостей. В каждом случае написать общее выражение координат произвольного нормального вектора: |
| | 923.1 | 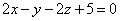 ; ; |
| | 923.2 | 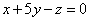 ; ; |
| | 923.3 | 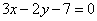 ; ; |
| | 923.4 | 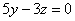 ; ; |
| | 923.5 | 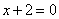 ; ; |
| | 923.6 | 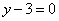 . .  |
| | | Установить, какие из следующих пар уравнений определяют параллельные плоскости: |
| | 924.1 | 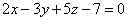 , , 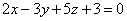 ; ; |
| | 924.2 | 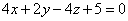 , , 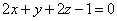 ; ; |
| | 924.3 | 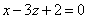 , , 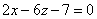 . . 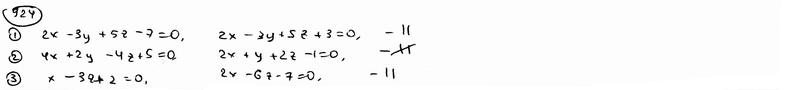 |
| | | Установить, какие из следующих пар уравнений определяют перпендикулярные плоскости: |
| | 925.1 | 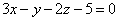 , , 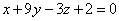 ; ; |
| | 925.2 | 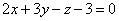 , , 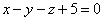 ; ; |
| | 925.3 | 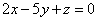 , , 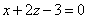 . . 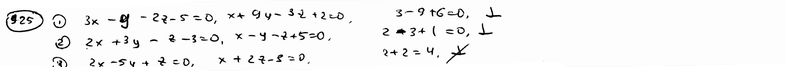 |
| | | Определить, при каких значениях l и m следующие пары уравнений будут определять параллельные плоскости: |
| | 926.1 | 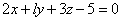 , , 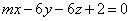 ; ; |
| | 926.2 | 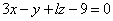 , , 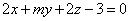 ; ; |
| | 926.3 | 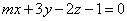 , , 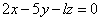 . . 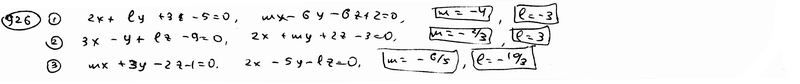 |
| | | Определить, при каких значениях l и m следующие пары уравнений будут определять перпендикулярные плоскости: |
| | 927.1 | 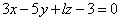 , , 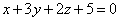 ; ; |
| | 927.2 | 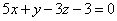 , , 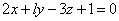 ; ; |
| | 927.3 | 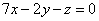 , , 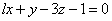 . . 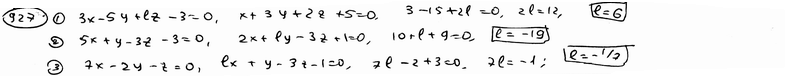 |
| | | Определить двугранные углы, образованные пересечением следующих пар плоскостей: |
| | 928.1 | 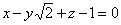 , , 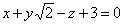 ; ; |
| | 928.2 | 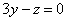 , , 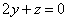 ; ; |
| | 928.3 | 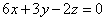 , , 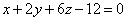 ; ; |
| | 928.4 | 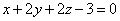 , , 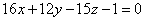 . .  |
| | | Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости 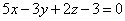 . .  |
| | | Составить уравнение плоскости, которая проходит через точку М1(3; -2; -7) параллельно плоскости 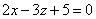 . . 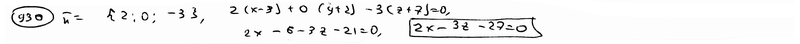 |
| | | Составить уравнение плоскости, которая проходит через начало координат перпендикулярно к двум плоскостям 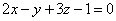 , , 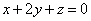 . . 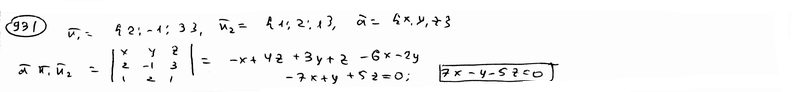 |
| | | Составить уравнение плоскости, которая проходит через точку М1(2; -1; 1) перпендикулярно к двум плоскостям 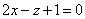 , , 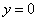 . . 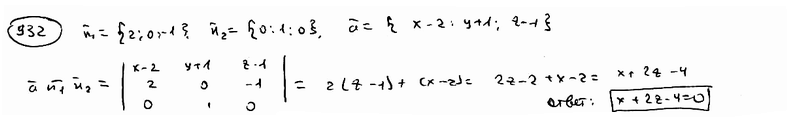 |
| | | Доказать, что уравнение плоскости, проходящей через точку М0(x0; y0; z0) перпендикулярно к плоскостям 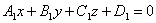 , , 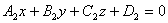 , может быть представлено в следующем виде: , может быть представлено в следующем виде: 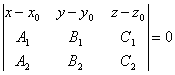 . .  |
| | | Составить уравнение плоскости, которая проходит через две точки М1(1; -1; -2), M2(3; 1; 1) перпендикулярно к плоскости 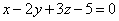 . . 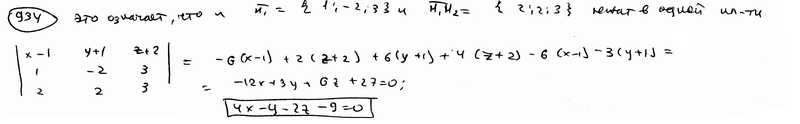 |
| | | Доказать, что уравнение плоскости, проходящей через две точки M1(x1; y1; z1), M2(x2, y2, z2) перпендикулярно к плоскости 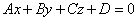 , может быть представлено в следующем виде: , может быть представлено в следующем виде: 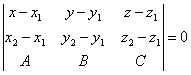 . . |
| | | Установить, что три плоскости 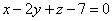 , , 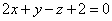 , , 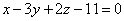 имеют общую точку, и вычислить ее координаты. имеют общую точку, и вычислить ее координаты. 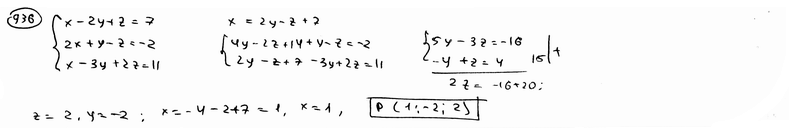 |
| | | Доказать, что три плоскости 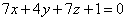 , , 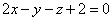 , , 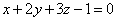 проходят через одну прямую. проходят через одну прямую. 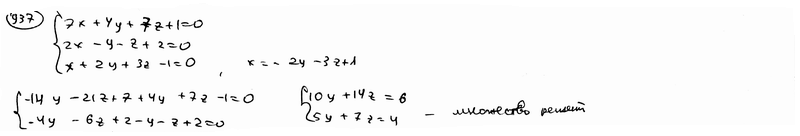 |
| | | Доказать, что три плоскости 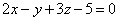 , , 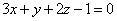 , , 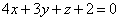 пересекаются по трем различным параллельным прямым. пересекаются по трем различным параллельным прямым.  |
| | | Определить, при каких значениях a и b плоскости 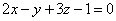 , , 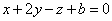 , , 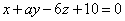 : : |
| | 939.1 | имеют одну общую точку; |
| | 939.2 | проходят через одну прямую; |
| | 939.3 | пересекаются по трем различным параллельным прямым.  Глава 39. Неполные уравнения плоскостей. Уравнения плоскости "в отрезках" Глава 39. Неполные уравнения плоскостей. Уравнения плоскости "в отрезках" | | | Составить уравнение плоскости, которая проходит: | | | 940.1 | через точку М1(2; -3; 3) параллельно плоскости Оху; | | | 940.2 | через точку М2(1; -2; 4) параллельно плоскости Oxz; | | | 940.3 | через точку М3(-5; 2; -1) параллельно плоскости Oyz.  | | | | Составить уравнение плоскости, которая проходит: | | | 941.1 | через ось Ох и точку М1(4; -1; 2); | | | 941.2 | через ось Oy и точку М2(1; 4; -3); | | | 941.3 | через ось Oz и точку М3(3; -4; 7); 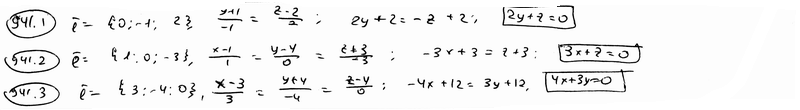 | | | | Составить уравнение плоскости, которая проходит: | | | 942.1 | через точки М1(7; 2; -3) и М2(5; 6; -4) параллельно оси Ох; | | | 942.2 | через точки P1(2; -1; 1) и P2(3; 1; 2) параллельно оси Оу; | | | 942.3 | через точки Q1(3; -2; 5) и Q2(2; 3; 1) параллельно оси Oz. 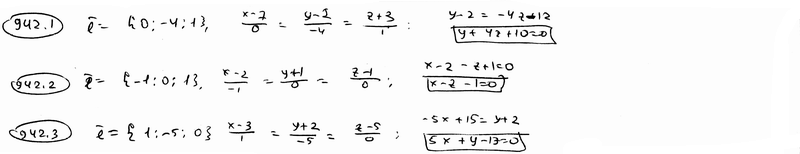 | | | | Найти точки пересечения плоскости 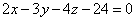 с координатными осями. с координатными осями. 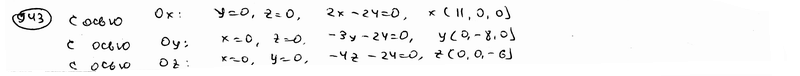 | | | | Дано уравнение плоскости 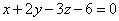 . Написать для нее уравнение в отрезках. . Написать для нее уравнение в отрезках.  | | | | Найти отрезки, отсекаемые плоскостью 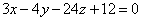 на координатных осях. на координатных осях. 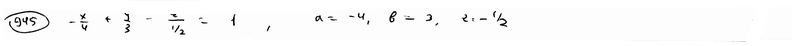 | | | | Вычислить площадь треугольника, который отсекает плоскость 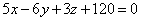 от координатного угла Оху. от координатного угла Оху. 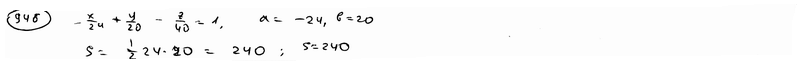 | | | | Вычислить объем пирамиды, ограниченной плоскостью 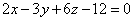 и координатными плоскостями. и координатными плоскостями. 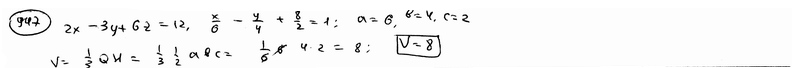 | | | | Плоскость проходит через точку М1(6; -10; 1) и отсекает на оси абсцисс отрезок a=-3 и на оси апликат отрезок c=2. Составить для этой плоскости уравнение в отрезках. 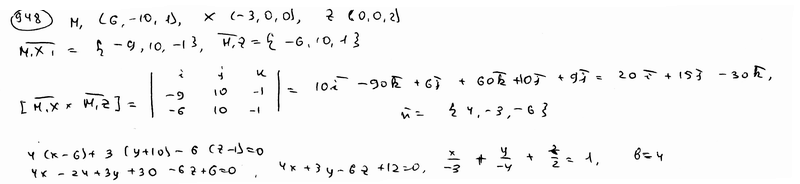 | | | | Плоскость проходит через точки М1(1; 2; -1) и M2(-3; 2; 1) и отсекает на оси ординат отрезок b=3. Составить для этой плоскости уравнение в отрезках.  | | | | Составить уравнение плоскости, которая проходит через точку М1(2; -3; -4) и отсекает на координатных осях отличные от нуля отрезки одинаковые величины (считая каждый отрезок направленными из начала координат). 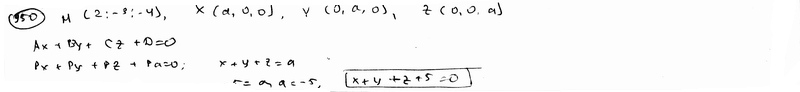 | | | | Составить уравнение плоскости, которая проходит через точки М1(-1; 4; -1), М2(-13; 2; -10) и отсекает на осях абсцисс и апликат отличные от нуля отрезки одинаковой длины. 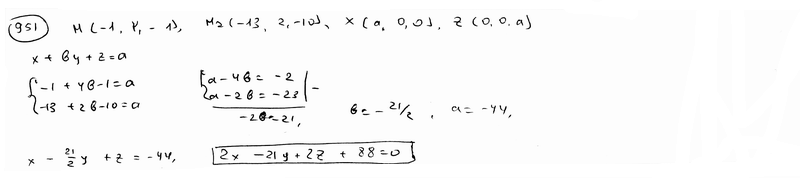 | | | | Составить уравнение плоскостей, которые проходят через точку М1(4; 3; 2) и отсекают на координатных осях отличные от нуля отрезки одинаковой длины. 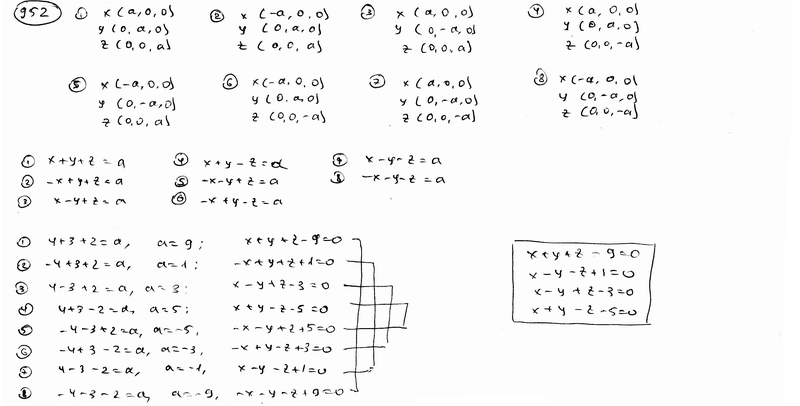 | | | | Составить уравнение плоскости, отсекающей на оси Oz отрезок c=-5 и перпендикулярной к ветору n={-2; 1; 3}. 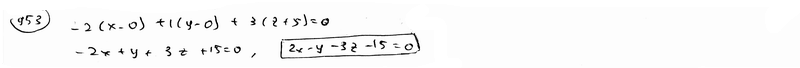 | | | | Составить уравнение плоскости, параллельной вектору l={2; 1; -1} и отсекающей на координатных осях Ох и Оу отрезки a=2, b=-2. 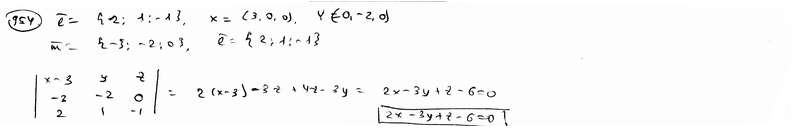 | | | | Составить уравнение плоскости, перпендикулярной к плоскости 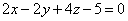 и отсекающей на координатных осях Ох и Оу отрезки a=-2, b=2/3. и отсекающей на координатных осях Ох и Оу отрезки a=-2, b=2/3. 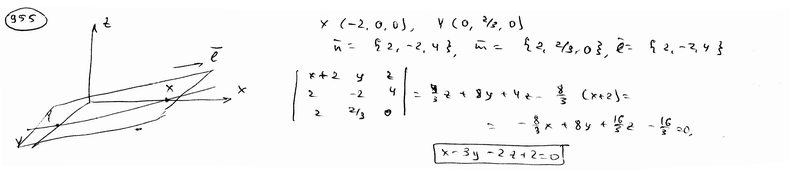 | |
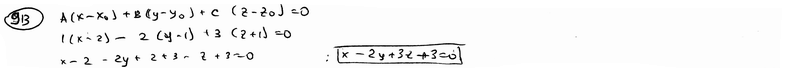

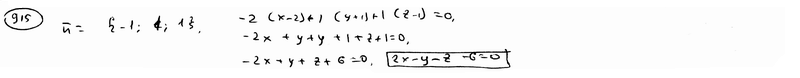
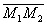 .
. 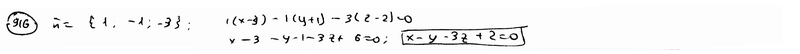
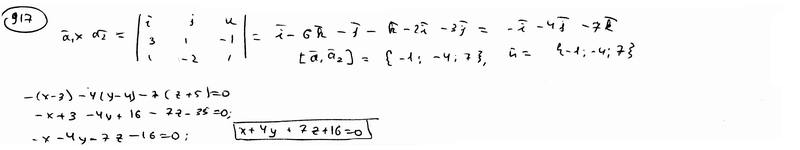
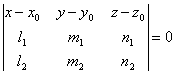 .
. 
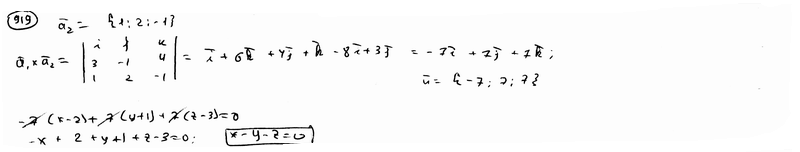
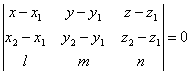 .
. 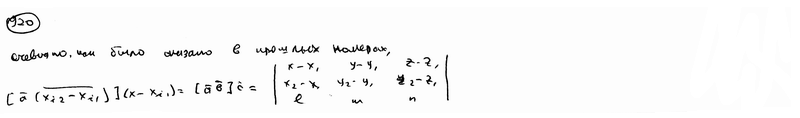

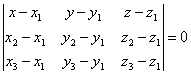 .
. 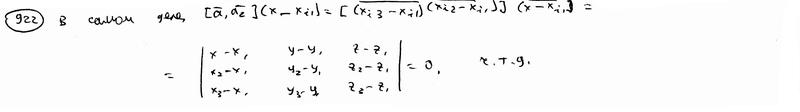
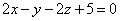 ;
; 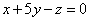 ;
; 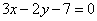 ;
; 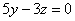 ;
; 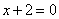 ;
; 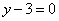 .
. 
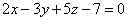 ,
, 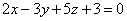 ;
; 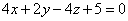 ,
, 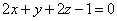 ;
; 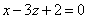 ,
, 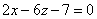 .
. 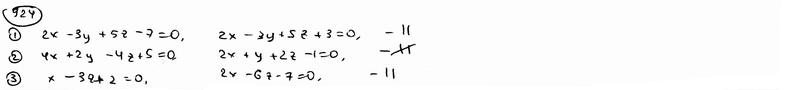
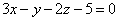 ,
, 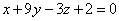 ;
; 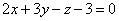 ,
, 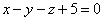 ;
; 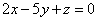 ,
, 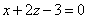 .
. 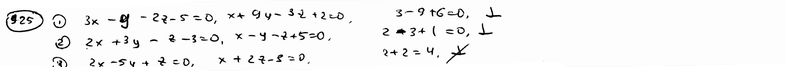
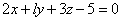 ,
, 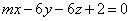 ;
; 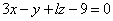 ,
, 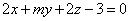 ;
; 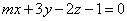 ,
, 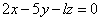 .
. 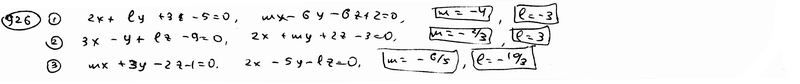
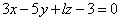 ,
, 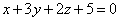 ;
; 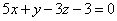 ,
, 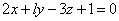 ;
; 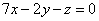 ,
, 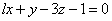 .
. 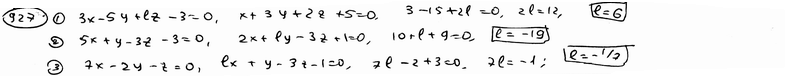
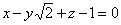 ,
, 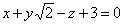 ;
; 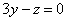 ,
, 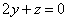 ;
; 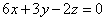 ,
, 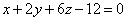 ;
; 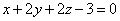 ,
, 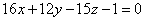 .
. 
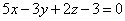 .
. 
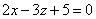 .
. 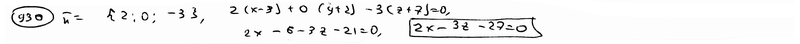
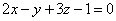 ,
, 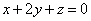 .
. 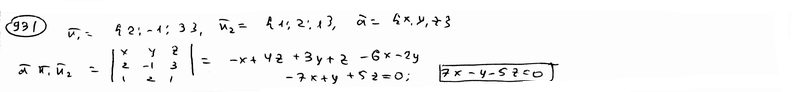
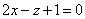 ,
, 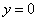 .
. 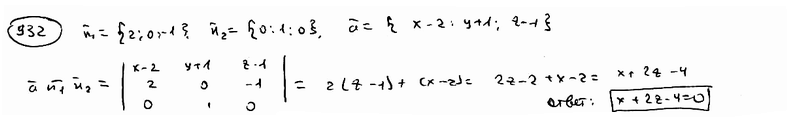
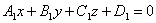 ,
, 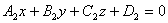 , может быть представлено в следующем виде:
, может быть представлено в следующем виде: 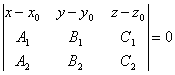 .
. 
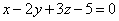 .
. 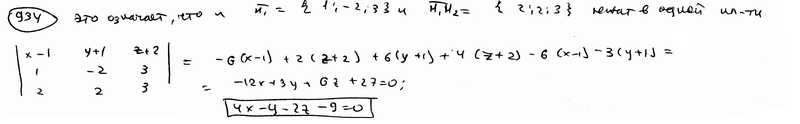
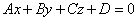 , может быть представлено в следующем виде:
, может быть представлено в следующем виде: 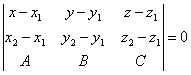 .
. 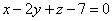 ,
, 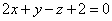 ,
, 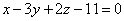 имеют общую точку, и вычислить ее координаты.
имеют общую точку, и вычислить ее координаты. 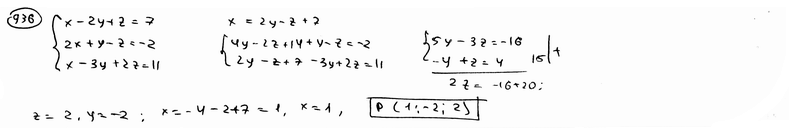
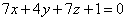 ,
, 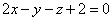 ,
, 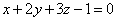 проходят через одну прямую.
проходят через одну прямую. 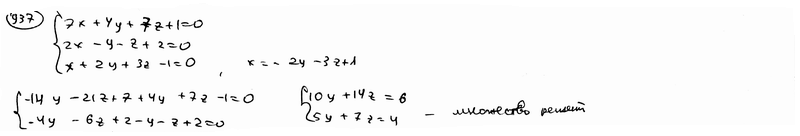
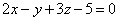 ,
, 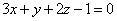 ,
, 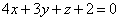 пересекаются по трем различным параллельным прямым.
пересекаются по трем различным параллельным прямым. 
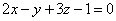 ,
, 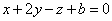 ,
, 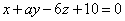 :
:  Глава 39. Неполные уравнения плоскостей. Уравнения плоскости "в отрезках"
Глава 39. Неполные уравнения плоскостей. Уравнения плоскости "в отрезках" 

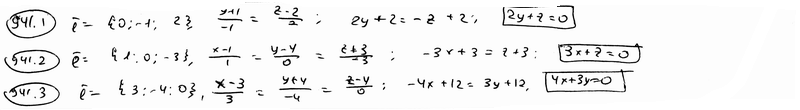
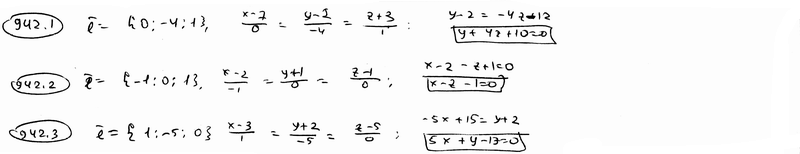
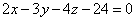 с координатными осями.
с координатными осями. 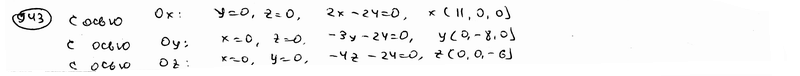
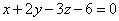 . Написать для нее уравнение в отрезках.
. Написать для нее уравнение в отрезках. 
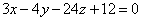 на координатных осях.
на координатных осях. 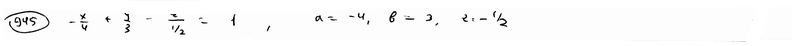
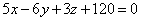 от координатного угла Оху.
от координатного угла Оху. 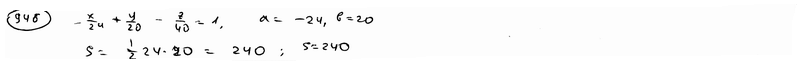
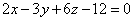 и координатными плоскостями.
и координатными плоскостями. 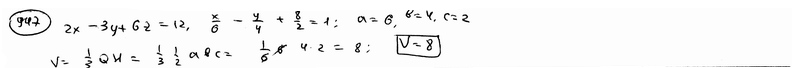


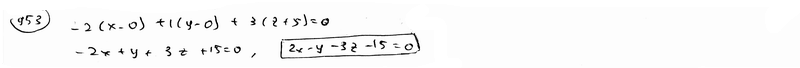
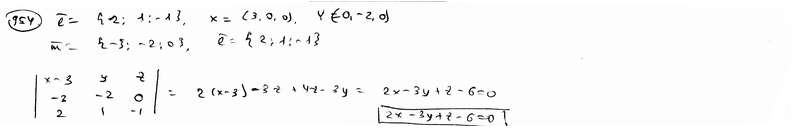
 и отсекающей на координатных осях Ох и Оу отрезки a=-2, b=2/3.
и отсекающей на координатных осях Ох и Оу отрезки a=-2, b=2/3.