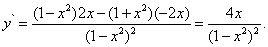Основные правила дифференцирования. дифференцируемы в некоторой точке , то в той же точке дифференцируемы и функции

Правило 1.Если функции

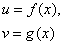
дифференцируемы в некоторой точке 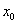, то в той же точке дифференцируемы и функции

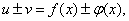
причём

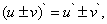(5)

т.е. производная алгебраической суммы функций равна алгебраической сумме производных этих функций.

Следствие. Если две дифференцируемые функции отличаются на постоянное слагаемое, то их производные равны, т.е.

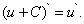(6)

Правило 2.Если функции

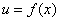
и

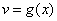
дифференцируемы в некоторой точке 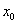, то в то же точке дифференцируемо и их произведение

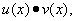
причём

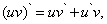(7)

т.е. производная произведения двух функций равна сумме произведений каждой из этих функций на производную другой.

Следствие 1. Постоянный множитель можно выносить за знак производной:

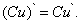(8)

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные.

Например, для трёх множителей имеем:

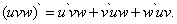(9)

Правило 3.Если функции

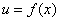
и

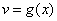
дифференцируемы в некоторой точке 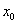и 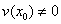, то в этой точке дифференцируемо и их частноеu/v , причём

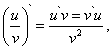(10)

т.е. производная частного двух функций равна дроби, числитель которой есть разность произведений знаменателя на производную числителя и числителя на производную знаменателя, а знаменатель есть квадрат прежнего числителя.

Пример 4.Найти производную функции

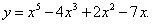
Решение. Применяя правила (5) и (8) и формулу (4) дифференцирования степенной функции получим

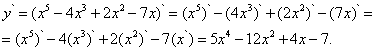
Пример 5.Найти производную функции

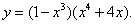
Решение. Применим правило (7) дифференцирования произведения, а затем найдём производные сомножителей так же, как в примере 4. Тогда получим

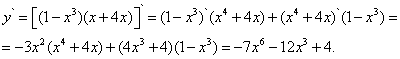
Пример 6.Найти производную функции

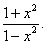
Решение. Применим правило (10) дифференцирования частного:

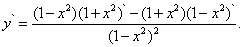
Затем, так же как и выше, вычислим производные в числителе. Имеем