Тема 8, 9. Розв’язування вправ на обчислення та застосування інтегралів
Приклад 1. Обчислити інтеграли:
а) 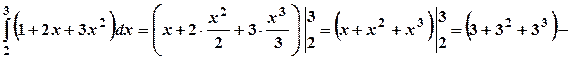
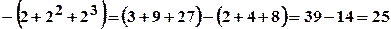 .
.
б) 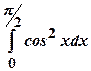 .
.
Первісну можна знайти, використавши формулу пониження степеня: 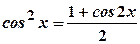 . Отримаємо:
. Отримаємо:
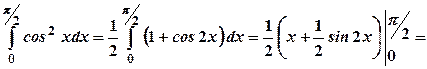
 .
.
Приклад 2.Дослідити на збіжність (розбіжність) і обчислити інтеграли:
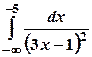 .
.
Згідно з формулою (2.2) будемо мати:
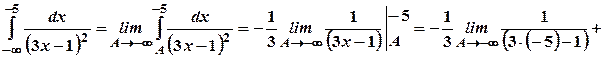
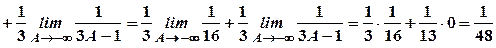 .
.
Границя скінчена, інтеграл збігається.
Приклад 3.Обчислити площі фігур, обмежених лініями.
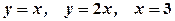 .
.
Рішення
Побудуємо дані лінії.
 Фігура на відрізку
Фігура на відрізку 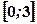 обмежена зверху
обмежена зверху 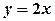 , знизу прямою
, знизу прямою 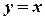 . Її площу знайдемо за формулою (3.3):
. Її площу знайдемо за формулою (3.3):
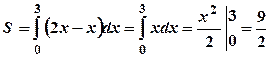 кв. од.
кв. од.
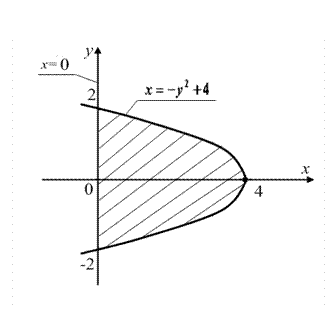
Приклад 4.Знайти об’єм тіла, утвореного обертанням навколо осі 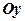 фігури, обмеженої лініями
фігури, обмеженої лініями 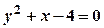 та
та 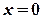 .
.
Рішення
Рівняння 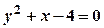 задає параболу з вершиною в точці
задає параболу з вершиною в точці 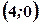 , віссю симетрії якої є вісь
, віссю симетрії якої є вісь 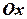 . Щоб знайти межі інтегрування, шукаємо ординати точок перетину ліній:
. Щоб знайти межі інтегрування, шукаємо ординати точок перетину ліній: 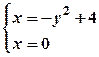 , тоді
, тоді 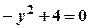 , звідки
, звідки 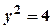 ,
, 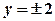 .
.
 Зважаючи на симетрію тіла відносно осі
Зважаючи на симетрію тіла відносно осі  , за формулою (5.5) маємо:
, за формулою (5.5) маємо:
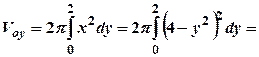
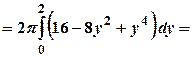
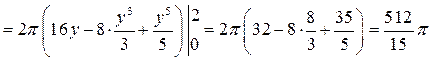 куб. од.
куб. од.
ПИТАННЯ ТА ЗАВДАННЯ ДЛЯ
САМОСТІЙНОГО
ОПРАЦЮВАННЯ МАТЕРІАЛУ
Тема 1, 2. Раціональні дроби та їх інтегрування.
Завдання для самоконтролю:
2.1.Представити неправильний дріб 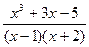 у вигляді суми многочленна та правильного раціонального дробу.
у вигляді суми многочленна та правильного раціонального дробу.
2.2. Обчислити інтеграли: а) 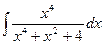 ; б)
; б) 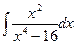 .
.
Питання для самоконтролю:
1. Поняття раціонального дробу.
2. Види елементарних (простіших) дробів.
3. Інтегрування раціональних дробів.
4. Назвати основні правила інтегрування.
5. Назвати основні методи інтегрування.
Тема 3, 4. Інтегрування виразів, що містять тригонометричні функції.
Завдання для самоконтролю:
4.1. Обчислити інтеграл: а) 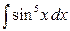 ; б)
; б) 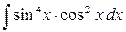
Питання для самоконтролю:
1. Обчислення інтегралів вигляду 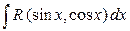 і
і 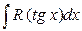 .
.
2. Обчислення інтегралів вигляду 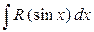 і
і 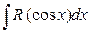 .
.
3. Обчислення інтегралів вигляду 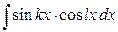 ,
, 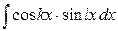 і
і 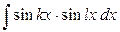 .
.
4. Коли застосовується метод інтегрування частинами ?
Тема 5. Невласні інтеграли.
Питання для самоконтролю:
1. Невласні інтеграли першого роду.
2. Ознаки збіжності невласних інтегралів першого роду.
3. Невласні інтеграли другого роду.
4. Ознаки збіжності невласних інтегралів другого роду.
Тема 6. Довжина дуги плоскої кривої.
Питання для самоконтролю:
1. Формула довжини дуги плоскої кривої заданої рівнянням 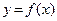 , що обмежена лініями
, що обмежена лініями 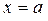 і
і 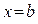 .
.
2. Формула довжини дуги кривої заданої параметрично.
Тема 7. Об’єм та площа поверхні тіла обертання.
Завдання для самоконтролю:
7.1. Знайти об’єм та поверхню тіла, утвореного обертанням кривої 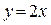 , обмеженої лініями
, обмеженої лініями 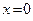 і
і 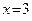 .
.
Питання для самоконтролю:
1. Застосування визначених інтегралів до обчислення об’ємів тіл обертання. 2. Застосування визначених інтегралів до обчислення поверхонь тіл обертання.
Тема 8, 9. Розв’язування вправ на обчислення та застосування інтегралів.
Завдання для самоконтролю:
9.1. Обчислити невизначений інтеграл: а) 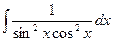 ; б)
; б) 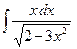 .
.
9.2 Обчислити визначений інтеграл: а) 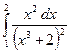 ; б)
; б) 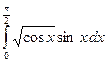 ;
;
в) 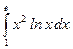
9.3. Обчислити невласний інтеграл: а) 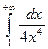 ; б)
; б) 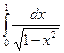 .
.
9.4. Знайти площу фігури, обмеженої лініями 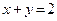 та
та 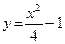 .
.
Питання для самоконтролю:
1. Назвати основні правила інтегрування.
2. Назвати основні методи інтегрування.
3. Формула Ньютона-Лебніца.
4. Ознаки збіжності невласних інтегралів першого роду.
5. Ознаки збіжності невласних інтегралів другого роду.
ЛІТЕРАТУРА:
1. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисления. – М.:Наука, 1981.
2. ДюженковаЛ.І., НосальТ.В. Вища математика. – К. : Вища школа.1991.
3. Шкіль М. І., Колесник Т. В., Котлова В.М. Вища математика. – К .:Вища школа,1984.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч.: Учебное пособие для втузов. – М.: Высшая школа, 2000.
5. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум: Навчальний посібник. – К.: Центр навчальної літератури, 2005.
6. Запорожец Г.И. Руководство к решению задач по математическому анализу: Учебное пособие для вузов. – М.: Высшая школа, 1966.
ВІДПОВІДІ ДО ЗАВДАНЬ САМОКОНТРОЛЮ:
2.1. 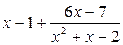 .
.
2.2. а) 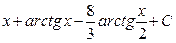 ; б)
; б) 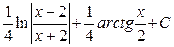 .
.
4.1. а) 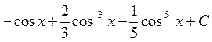 ; б)
; б) 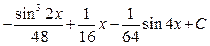 .
.
7.1. 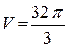 куб.од.,
куб.од., 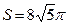 кв.од.
кв.од.
9.1. а) 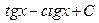 ; б)
; б) 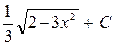
9.2. а) 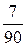 ; б)
; б) 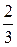 ; в)
; в) 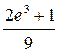
9.3. а) 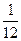 , збігається; б)
, збігається; б) 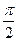 , збігається.
, збігається.
9.4. 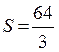 кв.од.
кв.од.
