Общее линейное уравнение с n неизвестными
КУРСОВАЯ РАБОТА
по дисциплине «Фундаментальная и компьютерная алгебра»
Решение систем линейных уравнений в целых числах
ОГУ 38.04.08. 3515. 022 00
Руководитель
доцент
_______ Носов В.В.
«__» _____________ 2016 г.
Студент группы 15МКН(ба)АПКМ
_______ Роговая Е. О.
«__» _____________ 2016 г.
Оренбург 2016
СОДЕРЖАНИЕ:
Введение
Уравнение с одним неизвестным.
Уравнения с двумя неизвестными.
Обобщенное уравнение с n неизвестными.
Системы двух уравнений с двумя неизвестными.
5.Системы трёх уравнений с тремя неизвестными.
Заключение.
Список литературы.
Введение Моя курсовая работа посвящена одному из разделов теории чисел – решению систем линейных уравнений в целых числах. Решение уравнений в целых числах является одной из древнейших математических задач. Проблема решения для уравнений с одним неизвестным не представляет существенного интереса, так как эта задача может быть решена с помощью конечного числа проб. Решение систем уравнений методом Гаусса не дает ответ в целых числах, в своей курсовой работе я рассматриваю краткий обзор алгоритмов построения минимального порождающего множества решений и базиса множества решений систем линейных диофантовых уравнений в целых числах. 1. Уравнение с одним неизвестным Рассмотрим уравнение с одним неизвестным 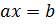 (1) Пусть коэффициенты уравнения a и b - целые числа, тогда (1) Пусть коэффициенты уравнения a и b - целые числа, тогда 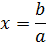 Решение этого уравнения будет целым числом тогда и только тогда, когда Решение этого уравнения будет целым числом тогда и только тогда, когда 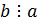 . Таким образом, уравнение (1) не всегда разрешимо в целых числах; так, например, из двух уравнений . Таким образом, уравнение (1) не всегда разрешимо в целых числах; так, например, из двух уравнений 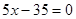 и и 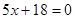 первое имеет целое решение, а второе в целых числах неразрешимо. 2. Уравнения с двумя неизвестными Рассмотрим уравнение первой степени с двумя неизвестными первое имеет целое решение, а второе в целых числах неразрешимо. 2. Уравнения с двумя неизвестными Рассмотрим уравнение первой степени с двумя неизвестными 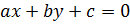 (2), где (2), где 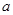 и и 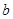 - целые числа, отличные от нуля, а - целые числа, отличные от нуля, а 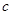 - произвольное целое. Будем считать, что коэффициенты - произвольное целое. Будем считать, что коэффициенты 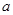 и и 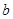 не имеют общих делителей, кроме единицы. Действительно, если НОД не имеют общих делителей, кроме единицы. Действительно, если НОД 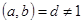 , то справедливы равенства , то справедливы равенства 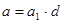 , , 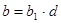 ; уравнение (2) принимает вид ; уравнение (2) принимает вид
и может иметь целые решения только в том случае, когда
Рассмотрим сначала случай, когда
Решая это уравнение относительно
Очевидно, что
где
и мы получаем формулы, содержащие все целые решения уравнения (2'):
Перейдем теперь к случаю Покажем, прежде всего, что для нахождения всех целых решений уравнения (2) достаточно найти какое-нибудь одно его решение, т. е. найти такие целые числа
Теорема. Пусть а и b взаимно просты и
Тогда формулы
при Доказательство. Пусть x,y - произвольное решение уравнения (2). Тогда из равенств
получаем
Так как
где
и получаем
Таким образом доказано, что всякое решение x, y имеет вид (3). Остается еще проверить, что всякая пара чисел x, y, получаемая по формулам (3) при целом
но так как Итак, если известно одно решение уравнения
Критерии: 1) При взаимно простых коэффициентах и при b=1 диофантово уравнение имеет решение в целых числах. 2) Если 3) Если в уравнении 4) Если в уравнении 5)Если в уравнении 6) Если пара целых чисел
где t – произвольное целое число, является общим решением этого уравнения в целых числах. |
Общее линейное уравнение с n неизвестными
Теорема. При взаимно простых коэффициентах 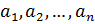 диофантово уравнение
диофантово уравнение 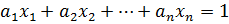 имеет решение в целых числах.
имеет решение в целых числах.
Доказательство.
Обозначим через M множество тех положительных чисел b, для которых уравнение 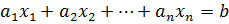 имеет решение в целых числах. M, очевидно, не пусто, так как при заданных
имеет решение в целых числах. M, очевидно, не пусто, так как при заданных 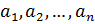 можно подобрать целые значения
можно подобрать целые значения 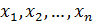 , такие, чтобы
, такие, чтобы 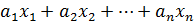 было положительным числом.
было положительным числом.
В множестве M существует наименьшее число (M– подмножество натуральных чисел), которое мы обозначим через d 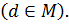 Обозначим через
Обозначим через 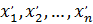 - целые числа, такие, что
- целые числа, такие, что 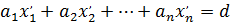
Пусть 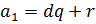 , где
, где 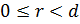 ; тогда
; тогда 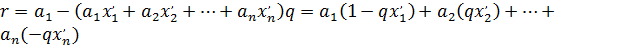
Мы подобрали целые значения: 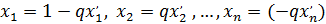 , такие, что
, такие, что 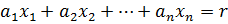 , но
, но 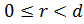 , а d - наименьшее положительное число в M, т. е. r не может быть положительным, r=0,
, а d - наименьшее положительное число в M, т. е. r не может быть положительным, r=0, 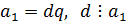 . Аналогично получаем:
. Аналогично получаем: 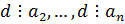 .
.
Мы видим, что d – общий делитель чисел 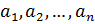 , следовательно, поскольку
, следовательно, поскольку 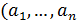 )=1 ,
)=1 , 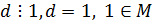 , то уравнение разрешимо в целых числах .
, то уравнение разрешимо в целых числах .
Теорема. Пусть d - наибольший общий делитель коэффициентов 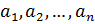 . Диофантово уравнение имеет решение тогда и только тогда, когда
. Диофантово уравнение имеет решение тогда и только тогда, когда 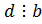 . Число решений такого уравнения равно либо нулю, либо бесконечности.
. Число решений такого уравнения равно либо нулю, либо бесконечности.
Докажем последовательно все три утверждения теоремы.
1) Пусть 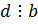 . Для уравнения
. Для уравнения 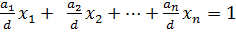 , где
, где 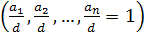 , существуют целые числа:
, существуют целые числа: 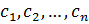 удовлетворяющие ему, т.е.
удовлетворяющие ему, т.е. 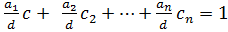 . Тогда
. Тогда 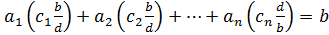 т. е.
т. е. 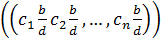 - решение уравнения.
- решение уравнения.
2) Пусть теперь d не делит b. Тогда левая часть уравнения при любых целых 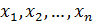 делится на d, а правая на d не делится, так что равенство при целых значениях
делится на d, а правая на d не делится, так что равенство при целых значениях 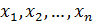 невозможно.
невозможно.
3) Если 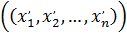 - упорядоченная последовательность чисел, удовлетворяющих уравнению, то, например,
- упорядоченная последовательность чисел, удовлетворяющих уравнению, то, например, 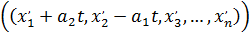 при
при 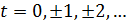 также удовлетворяют этому уравнению и, таким образом, либо совсем не будет решений, либо их будет бесконечное множество.
также удовлетворяют этому уравнению и, таким образом, либо совсем не будет решений, либо их будет бесконечное множество.
Если хоть одна пара коэффициентов взаимно простая, то d=1, и уравнение имеет бесчисленное множество решений.

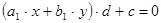
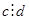 . Следовательно все коэффициенты уравнения (2) должны делиться нацело на
. Следовательно все коэффициенты уравнения (2) должны делиться нацело на 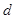 . Сокращая (2) на
. Сокращая (2) на 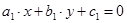 , где
, где 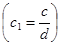 ,
, 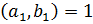
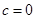 . Уравнение (2) примет вид:
. Уравнение (2) примет вид: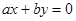 .
. 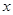 , получим
, получим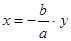 .
. 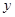 делится на
делится на 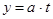 ,
, 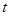 принимает произвольные целые значения
принимает произвольные целые значения 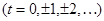 . Подставим это значение
. Подставим это значение 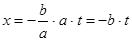 ,
,  ,
, 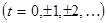 .
. 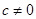 .
.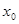 ,
, 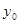 , для которых
, для которых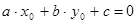 ,
, 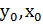 - какое-нибудь решение уравнения
- какое-нибудь решение уравнения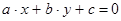 ,
, 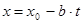 ,
, 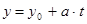
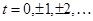 дают все решения уравнения (2).
дают все решения уравнения (2).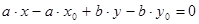 ;
; 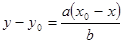 .
. 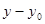 - целое число и числа
- целое число и числа 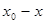 должно нацело делиться на
должно нацело делиться на 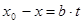 ,
, 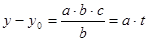 ,
, 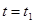 , будет решением уравнения(2).Чтобы провести такую проверку, подставим величины
, будет решением уравнения(2).Чтобы провести такую проверку, подставим величины 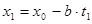 ,
, 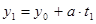 в левую часть уравнения (2):
в левую часть уравнения (2):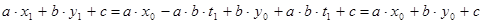 ,
, 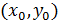 -решение, то
-решение, то 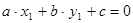 , т.е.
, т.е. 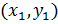 - решение уравнения (2), что и требовалось доказать.
- решение уравнения (2), что и требовалось доказать.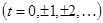 .
.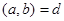 , то существуют такие целые числа x и y, что имеет место равенство
, то существуют такие целые числа x и y, что имеет место равенство 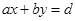
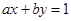 (4)
(4) 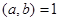 , то уравнение (4) имеет, по крайней мере, одно целое решение.
, то уравнение (4) имеет, по крайней мере, одно целое решение.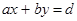 (5)
(5) 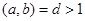 и c не делится на d, то уравнение целых решений не имеет.
и c не делится на d, то уравнение целых решений не имеет.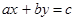 (6)
(6) 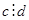 , то оно равносильно уравнению
, то оно равносильно уравнению 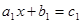 (6’), в котором
(6’), в котором 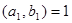 .
.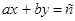 (6) , где
(6) , где 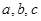 - целые числа, отличные от нуля и
- целые числа, отличные от нуля и 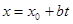 ,
, 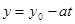 , (7)
, (7)