Кривые на плоскости и в пространстве
3.1. Параметрический способ задания кривой
Наиболее общим способом задания кривой является написание её уравнения в координатной или векторной формах (см. п.1.1.).
Координатная форма уравнения плоской кривой представляет собой систему
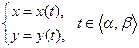 , (1)
, (1)
где 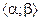 ,
, 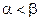 , – некоторый промежуток, а
, – некоторый промежуток, а 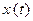 и
и 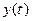 – определенные на нем функ- ции. Система (1) каждому t,
– определенные на нем функ- ции. Система (1) каждому t, 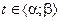 сопоставляет точку плоскости
сопоставляет точку плоскости 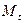 с абсциссой
с абсциссой 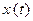 и ординатой
и ординатой 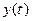 . Когда t, возрастая, пробегает отрезок
. Когда t, возрастая, пробегает отрезок 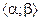 , точка
, точка 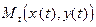 перемещается по плоскости; траектория, описываемая ею, и есть кривая G (рис.3.1).
перемещается по плоскости; траектория, описываемая ею, и есть кривая G (рис.3.1).
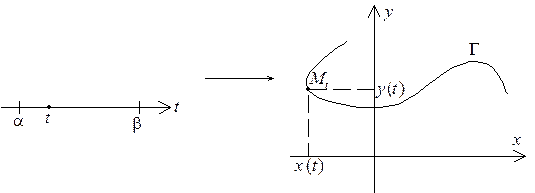
Рис. 3.1.
Система
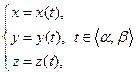 ( 2 ) есть координатная форма уравнения кривой G, расположенной в пространстве. Она каждому t,
( 2 ) есть координатная форма уравнения кривой G, расположенной в пространстве. Она каждому t, 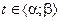 , ставит в соответствие точку
, ставит в соответствие точку 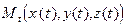 , а кривая G есть траектория, которую описывает
, а кривая G есть траектория, которую описывает 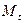 , когда t, возрастая, пробегает отрезок
, когда t, возрастая, пробегает отрезок 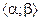 (рис. 3.2). Уравнения
(рис. 3.2). Уравнения 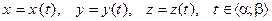 , входящие в систему (2), называют параметрическими уравнениями кривой Г
, входящие в систему (2), называют параметрическими уравнениями кривой Г
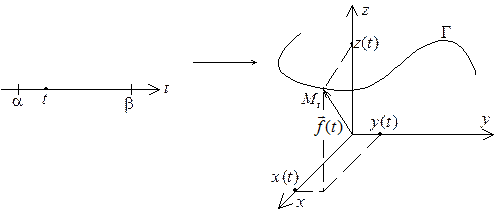
Рис. 3.2.
Уравнение (1) плоской кривой можно считать частным случаем уравнения (2) при 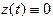 на
на 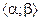 ; поэтому ниже, в основном, рассматриваем кривые, заданные уравнением (2). Это уравнение чаще записываем в векторной форме:
; поэтому ниже, в основном, рассматриваем кривые, заданные уравнением (2). Это уравнение чаще записываем в векторной форме:
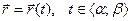 , (3)
, (3)
где 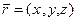 ,
, 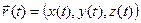 . Заметим, что кривая G является годографом век- тор- функции
. Заметим, что кривая G является годографом век- тор- функции 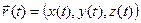
Ниже функции 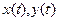 и
и 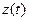 , а, следовательно, и вектор- функцию
, а, следовательно, и вектор- функцию 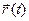 , счи- таем непрерывными на
, счи- таем непрерывными на 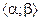 .
.
Пусть кривая Г задана уравнением (3).
Определение. Кривую Г назовём элементарной кривой, если из условия 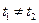 , следует
, следует 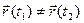
.Уравнение кривой задает отображение отрезка 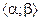 числовой оси на множест- во точек плоскости или пространства, принадлежащих кривой. Это отображение непрерывно ( так как
числовой оси на множест- во точек плоскости или пространства, принадлежащих кривой. Это отображение непрерывно ( так как 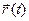 непрерывная функция), а в случае элементарной кривой оно ещё и взаимно однозначно.
непрерывная функция), а в случае элементарной кривой оно ещё и взаимно однозначно.
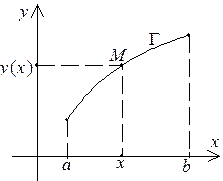 Рис. 3.3. Рис. 3.3. |
Пример 3. Пусть плоская кривая G является графиком функции 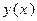 , непрерывной на промежутке
, непрерывной на промежутке 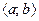 ,
, 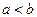 :
: 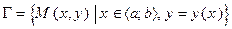 (рис.3.3). Уравнение этой кривой можно записать в явной форме
(рис.3.3). Уравнение этой кривой можно записать в явной форме 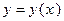 ; можно записать для нее параметрические уравнения:
; можно записать для нее параметрические уравнения:
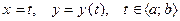 .
.
Очевидно, график G есть элементарная кривая.
Определение. Точку P, 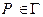 , назовем кратной точкой кривой или точкой самопересечения, если существуют
, назовем кратной точкой кривой или точкой самопересечения, если существуют 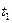 и
и 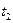 ,
, 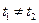 , принадлежащие
, принадлежащие 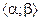 и такие, что точки
и такие, что точки 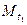 и
и 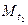 совпадают с P (следовательно,
совпадают с P (следовательно, 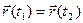 ).
).
Пример 1. Рассмотрим плоскую кривую G, заданную системой
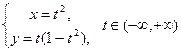 .
.
Эта кривая изображена на рис.3.4. При возрастании t точка 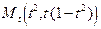 описывает G, двигаясь в направлении, указанном на рисунке стрелками. При
описывает G, двигаясь в направлении, указанном на рисунке стрелками. При 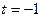 она проходит через точку
она проходит через точку 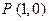 ; описав петлю, она снова проходит через точку P при
; описав петлю, она снова проходит через точку P при 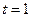 . P – точка самопересечения кривой G.
. P – точка самопересечения кривой G.
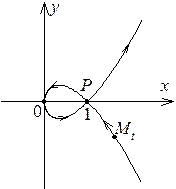 Рис. 3.4. Рис. 3.4. |
Кривая, имеющая хотя бы одну точку самопересечения, не является элементарной .
Замечание. Если хотя бы одна из координатных функций 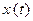 ,
, 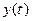 и
и 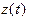 строго монотонна на
строго монотонна на 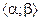 , то кривая G, заданная уравнением (3), является элементарной кривой. Дей- ствительно, пусть, к примеру,
, то кривая G, заданная уравнением (3), является элементарной кривой. Дей- ствительно, пусть, к примеру, 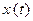 , строго моно- тонна. Тогда для любых
, строго моно- тонна. Тогда для любых 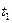 и
и 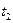 ,
, 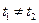 , лежащих на
, лежащих на 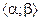 , будет выполнено
, будет выполнено 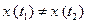 , а этого достаточно, чтобы утверждать:
, а этого достаточно, чтобы утверждать: 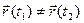 .
.
3.2. Касательная к кривой
В п.1.5. главы 2 было введено понятие о касательной к графику функции 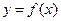 : касательная есть предельное положение секущей. Здесь мы определим это понятие для кривой, представленной параметрически и расположенной, вообще говоря, в пространстве.
: касательная есть предельное положение секущей. Здесь мы определим это понятие для кривой, представленной параметрически и расположенной, вообще говоря, в пространстве.
Пусть G - элементарная кривая, заданная уравнением (3), где вектор- функция 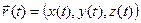 непрерывна на
непрерывна на 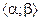 ,
, 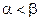 .
.
Зафиксируем некоторое число 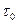 ,
, 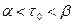 , и определим для
, и определим для 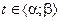 и
и 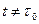 вектор- функцию
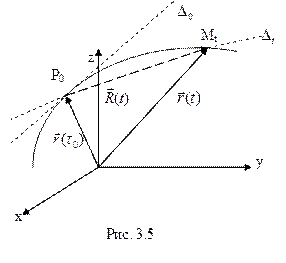
вектор- функцию 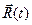 :
: 

Так как G – элементарная кривая, то при 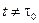
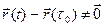 , поэтому
, поэтому 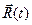 определена при
определена при 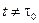 , причём
, причём 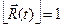 ( рис. 3.5.).
( рис. 3.5.).
Допустим, что существует предел 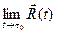 ; обозначим этот предел через
; обозначим этот предел через 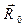 . Обозначим также через
. Обозначим также через 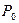 точку с координатами
точку с координатами 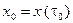 ,
, 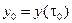 и
и 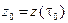 (рис. 3.5).
(рис. 3.5).
Определение 2. Касательной к кривой G в точке 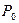 назовем прямую
назовем прямую 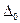 , проходящую через точку
, проходящую через точку 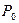 параллельно вектору
параллельно вектору 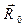 .
.
Замечание. Прямую 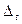 , проходящую через точки
, проходящую через точки 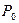 и
и 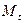 (
( 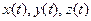 ),
), 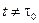 , называют секущей. Вектор
, называют секущей. Вектор 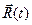 – направляющий вектор секущей
– направляющий вектор секущей 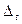 (рис. 3.5). При
(рис. 3.5). При 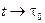 секущая
секущая 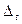 вращается вокруг точки
вращается вокруг точки 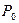 так, что угол между
так, что угол между 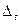 и
и 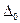 стремится к нулю. Имея в виду это обстоятельство, касательную
стремится к нулю. Имея в виду это обстоятельство, касательную 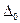 называют предельным положением секущей
называют предельным положением секущей 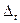 при
при 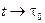 .
.
Определение 2 имеет смысл, если существует 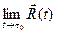 . Между тем, этот предел существует не всегда.
. Между тем, этот предел существует не всегда.
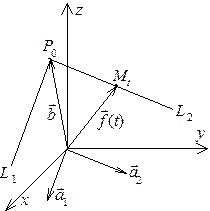 Рис. 3.6. Рис. 3.6. |
Пример 1. Пусть 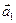 ,
, 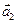 и
и 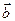 – заданные векторы, причем
– заданные векторы, причем 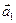 и
и 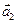 отличны от нуля и неколлинеарны. Обозначим через
отличны от нуля и неколлинеарны. Обозначим через 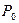 точку, радиусом-вектором которой является
точку, радиусом-вектором которой является 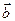 . Рассмотрим кривую G, уравнение которой
. Рассмотрим кривую G, уравнение которой
,
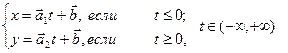
G состоит из двух лучей с общей вершиной 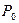 : луча
: луча 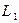 , параллельного
, параллельного 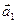 и луча
и луча 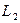 , параллельного
, параллельного 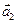 (рис.3.6). При всех
(рис.3.6). При всех 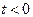 точка
точка 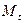 лежит на
лежит на 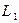 , поэтому при
, поэтому при 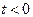 вектор
вектор 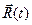 коллинеарен
коллинеарен 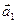 ; при
; при 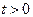
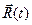 коллинеарен
коллинеарен 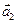 . Отсюда ясно, что односторонние пределы в точке
. Отсюда ясно, что односторонние пределы в точке 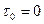 различны, поэтому
различны, поэтому 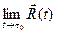 не существует. Следовательно, касательной к G в точке
не существует. Следовательно, касательной к G в точке 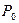 нет.
нет.
Итак, касательная существует не всегда.
Теорема 1. (О существовании касательной) Пусть вектор- функция 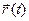 в урав- нении (3) непрерывно дифференцируема в точке
в урав- нении (3) непрерывно дифференцируема в точке 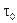 ,
, 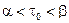 , причём
, причём 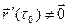 . Тог- да:
. Тог- да:
1) существует касательная 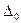 к кривой G в точке
к кривой G в точке 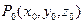 , где
, где 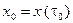 ,
, 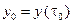 ,
, 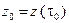 ;
;
2) уравнение 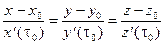 , есть уравнение касательной
, есть уравнение касательной 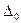
► Так как 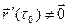 , то хотя бы одна из координат
, то хотя бы одна из координат 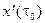 ,
, 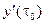 ,
, 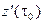 век- тора
век- тора 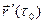 отлична от нуля. Для определенности будем считать, что
отлична от нуля. Для определенности будем считать, что 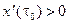 . Функ- ция
. Функ- ция 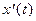 – непрерывна в точке
– непрерывна в точке 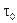 , поэтому найдется
, поэтому найдется 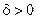 такое, что
такое, что 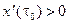 на ин- тервале
на ин- тервале 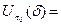
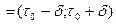 . Значит,
. Значит, 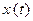 возрастает на этом интервале. Отсюда следует (см. замечание, п.3.1,): при любых
возрастает на этом интервале. Отсюда следует (см. замечание, п.3.1,): при любых 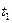 и
и 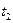 ,
, 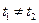 , лежащих на интервале
, лежащих на интервале 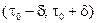 ,справедливо
,справедливо 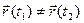 .
.
1) В проколотой окрестности 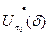 рассмотрим вектор- функцию
рассмотрим вектор- функцию 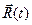 :
:

Пусть 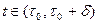 . Имеем:
. Имеем: 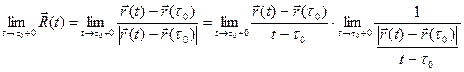 .
.
Вектор-функция 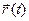 дифференцируема в точке
дифференцируема в точке 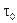 , поэтому
, поэтому
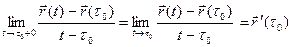 ;
;
отсюда: 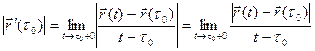 .
.
Итак, 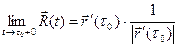 .
.
Аналогично получим:
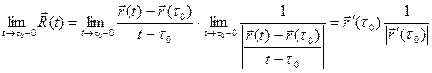 .
.
Так как односторонние пределы одинаковы, то предел 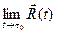 существует и равен
существует и равен 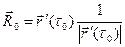 . Следовательно, касательная в точке Р0 существует: это прямая
. Следовательно, касательная в точке Р0 существует: это прямая 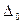 , проходящая через
, проходящая через 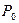 параллельно
параллельно 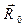
2) Запишем каноническое уравнение прямой 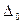 . Она проходит через точку
. Она проходит через точку 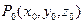 , а вектор
, а вектор 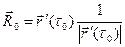 является её направляющим вектором. Очевидно, что векторы
является её направляющим вектором. Очевидно, что векторы 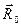 и
и 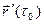 сонаправлены; поэтому в качестве направляющего вектора прямой
сонаправлены; поэтому в качестве направляющего вектора прямой 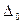 можно взять
можно взять 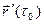
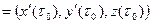 . Значит, каноническое уравнение
. Значит, каноническое уравнение 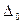 запишется так:
запишется так: 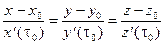 .
. 
Замечание . В процессе доказательства теоремы установлено, что вектор 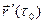 является направляющим вектором касательной
является направляющим вектором касательной 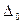 . В этом состоит геометрический смысл производной вектор- функции..
. В этом состоит геометрический смысл производной вектор- функции..
Определение. Кривую G, заданную представлением (3), называют гладкой кри- вой, если
1) вектор-функция 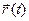 непрерывно дифференцируема на
непрерывно дифференцируема на 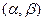 ;
;
2) 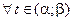
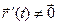 .
.
Из этого определения и доказанной теоремы вытекает, что в каждой точке глад- кой кривой существует касательная к ней. Кроме того, так как производная 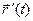 , определяющая направление касательной, непрерывна на
, определяющая направление касательной, непрерывна на 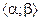 , на кривой нет “угло- вых” точек - точек, при переходе через которые направление касательной меняется скачком. В этом состоит геометрический смысл определения гладкой кривой. Геометрически гладкая кривая – это кривая, имеющая в каждой точке касательную, положение которой при движении точки вдоль кривой изменяется плавно.
, на кривой нет “угло- вых” точек - точек, при переходе через которые направление касательной меняется скачком. В этом состоит геометрический смысл определения гладкой кривой. Геометрически гладкая кривая – это кривая, имеющая в каждой точке касательную, положение которой при движении точки вдоль кривой изменяется плавно.
Определение. Плоскость, проходящую через точку 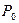 ,
, 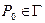 , перпендикулярно касательной
, перпендикулярно касательной 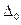 к G в точке
к G в точке 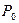 , называют нормальной плоскостью кривой G в точке
, называют нормальной плоскостью кривой G в точке 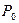 . Всякую прямую, проходящую через
. Всякую прямую, проходящую через 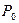 перпендикулярно
перпендикулярно 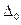 , называют нормалью кривой G в точке
, называют нормалью кривой G в точке 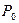 .
.
Если G задана представлением (3), то уравнение нормальной плоскости к G в точке 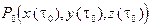 запишется так:
запишется так:
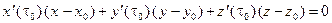 .
.
Остановимся отдельно на случае, когда G есть плоская кривая, являющаяся графиком функции 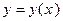 на промежутке
на промежутке 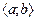 ,
, 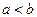 . Система
. Система
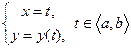
есть координатная форма уравнения Г , а
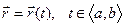 ,
,
где 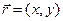 ,
, 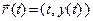 есть векторная форма её уравнения. Если
есть векторная форма её уравнения. Если 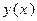 имеет на
имеет на 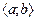 непрерывную производную
непрерывную производную 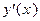 , то производная
, то производная 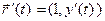 непрерывна и отлична от
непрерывна и отлична от 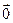 на
на 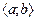 ; поэтому Г удовлетворяет требованиям определения гладкой кривой.. Пусть
; поэтому Г удовлетворяет требованиям определения гладкой кривой.. Пусть 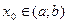 ,
, 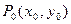 , где
, где 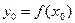 . Запишем уравнение касательной к G в точке
. Запишем уравнение касательной к G в точке 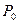 (см. утверждение 2) теоремы):
(см. утверждение 2) теоремы):
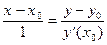 , т.е.
, т.е. 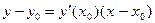
(сравните с уравнением касательной, полученным в п.1.5. гл. 2).
3.3. Длина кривой
Пусть кривая G задана уравнением
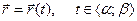 , (3)
, (3)
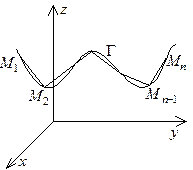 Рис. 3.8. Рис. 3.8. |
где вектор-функция 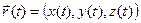 непрерывна на
непрерывна на 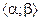 ,
, 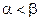 . Обозначим через T некоторый набор
. Обозначим через T некоторый набор 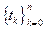 чисел, лежащих на
чисел, лежащих на 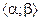 :
: 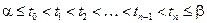 . Введем также следующие обозначения:
. Введем также следующие обозначения: 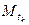 – точка с координата- ми
– точка с координата- ми 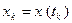 ,
, 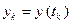 ,
, 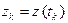 ,
, 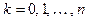 ;
; 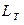 – ломаная линия, звеньями которой являются прямолиней- ные отрезки
– ломаная линия, звеньями которой являются прямолиней- ные отрезки 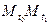 ,
, 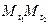 ,
, 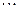 ,
, 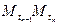 . Вершины ло- маной
. Вершины ло- маной 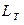 , точки
, точки 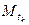 ,
, 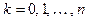 , лежат на G, мы будем говорить, что ломаная
, лежат на G, мы будем говорить, что ломаная 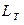 вписана в кривую G (рис.3.8). Через
вписана в кривую G (рис.3.8). Через 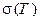 обозначим длину ломаной
обозначим длину ломаной 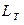 :
:
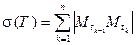 .
.
Определение 1. Длиной кривой G назовем точную верхнюю грань длин всевозможных ломаных, вписанных в G.
Обозначать длину G будем через 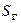 . Таким образом, по определению
. Таким образом, по определению
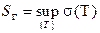 ,
,
где 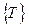 есть совокупность всевозможных наборов чисел
есть совокупность всевозможных наборов чисел 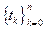 таких, что
таких, что 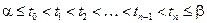 ; здесь n принимает любые натуральные значения.
; здесь n принимает любые натуральные значения.
Величина 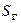 – либо положительное число, либо
– либо положительное число, либо 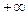 . Достаточно ясно, напри- мер, что в такую неограниченную кривую, как парабола, можно вписать ломаную
. Достаточно ясно, напри- мер, что в такую неограниченную кривую, как парабола, можно вписать ломаную 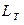 как угодно большой длины
как угодно большой длины 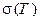 ; поэтому для параболы
; поэтому для параболы 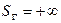 .
.
Определение. Кривую G назовем спрямляемой кривой, если ее длина 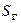 есть неотрицательное число (т.е. если
есть неотрицательное число (т.е. если 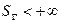 ).
).
Введем обозначения, которые используются ниже. Пусть вектор-функция 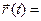
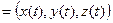 непрерывно дифференцируема на сегменте
непрерывно дифференцируема на сегменте 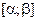 Тогда функции
Тогда функции 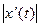 ,
, 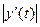 и
и 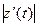 непрерывны, а потому и ограничены на
непрерывны, а потому и ограничены на 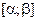 . Обозначим через
. Обозначим через 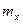 ,
, 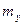 и
и 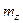 точные нижние грани на
точные нижние грани на 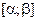 функций
функций 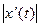 ,
, 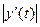 и
и 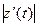 соотвеетст- венно, а через
соотвеетст- венно, а через 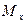 ,
, 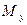 и
и 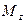 – точные верхние грани на
– точные верхние грани на 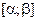 этих функций.
этих функций.
Теорема 1.( Достаточный признак спрямляемости кривой) Пусть кривая G, задана уравнением (3), где 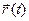 непрерывно дифференцируема на сегменте
непрерывно дифференцируема на сегменте 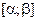 . Тогда G спрямляема, а ее длина удовлетворяет неравенствам:
. Тогда G спрямляема, а ее длина удовлетворяет неравенствам:
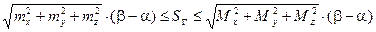 . (4)
. (4)
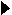 Пусть
Пусть 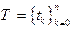 ,
, 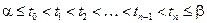 . Запишем выражение для длины
. Запишем выражение для длины 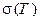 ломаной
ломаной 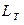 , вписанной в кривую G:
, вписанной в кривую G:
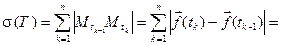
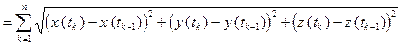 .
.
По формуле конечных приращений (теорема 4, п. 2.2, гл. 2) на сегменте 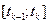 найдутся точки
найдутся точки 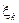 ,
, 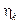 и
и 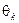 такие, что
такие, что 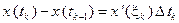 ,
, 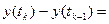
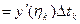 ,
, 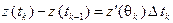 , где
, где 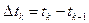 . Отсюда:
. Отсюда:
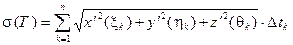 . ( 5)
. ( 5)
Так как  ,
, 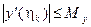 и
и 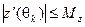 , то
, то
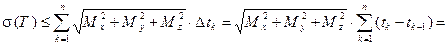
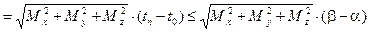 .
.
Неравенство 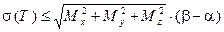 справедливо для всякого набора T, поэтому
справедливо для всякого набора T, поэтому
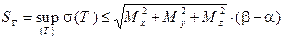 .
.
Тем самым доказаны спрямляемость кривой G и правая часть неравенств (4). Докажем левую часть этих неравенств. Из (5) имеем:
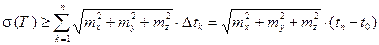 .
.
Совокупность 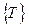 содержит всевозможные наборы
содержит всевозможные наборы 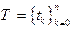 ; среди этих наборов имеются такие, для которых
; среди этих наборов имеются такие, для которых 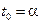 и
и 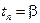 . Если набор
. Если набор 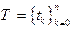 удовлетворяет условиям
удовлетворяет условиям 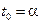 и
и 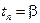 , то
, то 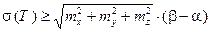 , поэтому и
, поэтому и 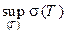 не меньше
не меньше 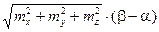 , т.е.
, т.е. 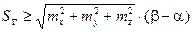 .
. 
3.4. Уравнение с натуральным параметром
Пусть G – спрямляемая кривая, заданная уравнением (3). где вектор-функция 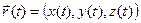 непрерывно дифференцируема на сегменте
непрерывно дифференцируема на сегменте 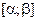 ,
, 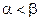 .
.
Обозначим через 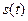 длину дуги, ограниченной точками
длину дуги, ограниченной точками 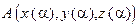 и
и 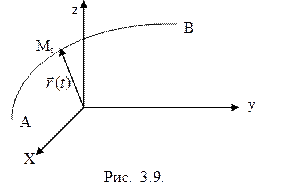
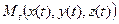 (рис. 3.9). Величину
(рис. 3.9). Величину 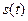 будем рассматривать как функцию аргумента t, заданную на сегменте
будем рассматривать как функцию аргумента t, заданную на сегменте 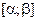 . Эту функцию называют переменной длиной дуги. Заметим:
. Эту функцию называют переменной длиной дуги. Заметим: 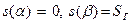 .
.
Теорема.(О переменной длине дуги) Переменная длина дуги 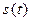 дифференцируема на
дифференцируема на 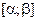 , причем
, причем 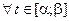
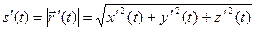 .
.
 Пусть
Пусть 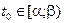 ,
, 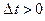 и такое, что
и такое, что 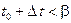 . Обозначим:
. Обозначим: 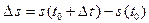 .
. 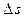 есть длина дуги кривой G, которую пробегает точка
есть длина дуги кривой G, которую пробегает точка 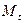 при возрастании t от
при возрастании t от 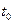 до
до 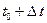 . По теореме о достаточном признаке спрямляемости
. По теореме о достаточном признаке спрямляемости
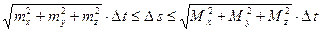 , (6)
, (6)
где 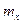 ,
, 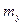 и
и 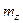 – точные нижние грани
– точные нижние грани 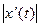 ,
, 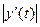 и
и 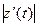 на
на 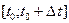 , а
, а 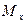 ,
, 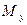 и
и 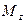 – точные верхние грани на
– точные верхние грани на 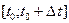 тех же функций. Так как указан- ные функции непрерывны на
тех же функций. Так как указан- ные функции непрерывны на 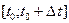 , существуют лежащие на
, существуют лежащие на 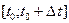 точки
точки 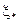 ,
, 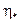 и
и 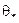 , такие, что
, такие, что 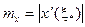 ,
, 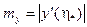 ,
, 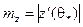 , а также точки
, а также точки 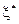 ,
, 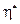 , и
, и 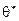 , такие, что
, такие, что 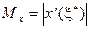 ,
, 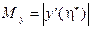 ,
, 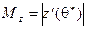 . Из (6) теперь получим:
. Из (6) теперь получим:
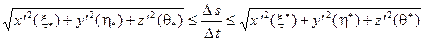 .
.
При 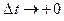 , каждая из точек
, каждая из точек 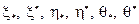 стремится к
стремится к 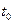 справа, поэтому, так как
справа, поэтому, так как 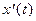 ,
, 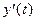 и
и 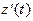 непрерывны в точке
непрерывны в точке 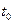 , получим:
, получим:
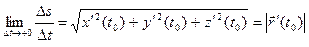 .
.
Здесь 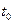 – произвольное число из
– произвольное число из 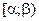 ; значит,
; значит, 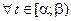
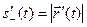 . (7)
. (7)
Пусть теперь 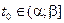 ,
, 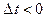 и такое, что
и такое, что 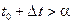 Заметим, что при
Заметим, что при 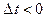 приращение
приращение 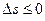 . Аналогично изложенному выше получим:
. Аналогично изложенному выше получим:
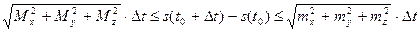 , (8)
, (8)
где 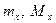 ,
, 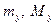 и
и 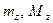 – точные грани на
– точные грани на 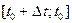 функций
функций 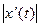 ,
, 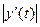 и
и 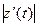 соответственно. Поделив все части (8) на отрицательное число
соответственно. Поделив все части (8) на отрицательное число 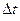 , получим:
, получим:
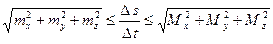 . (9)
. (9)
На 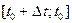 существуют точки
существуют точки 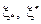 ,
, 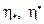 и
и 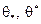 , в которых
, в которых 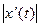 ,
, 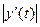 ,
, 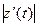 достигает своих точных нижних и верхних граней. Из (9) имеем:
достигает своих точных нижних и верхних граней. Из (9) имеем:
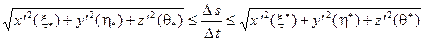 .
.
Перейдя здесь к пределу при 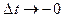 , получим:
, получим:
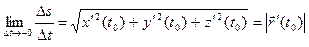 .
.
Здесь 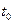 – произвольное число из
– произвольное число из 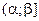 ; следовательно, доказано:
; следовательно, доказано: 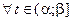
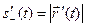 . (10)
. (10)
Из (7) и (10) вытекает: 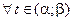
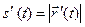 . Кроме того,
. Кроме того, 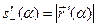 (см. (7) и
(см. (7) и 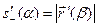 (см. 10)). Таким образом, утверждение теоремы справедливо.
(см. 10)). Таким образом, утверждение теоремы справедливо. 
Пусть кривая G, заданная представлением (3) является гладкой. Тогда 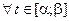
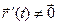 . Но
. Но 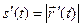 ; значит,
; значит, 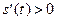 на
на 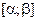 , и функция
, и функция 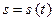 возрастает на
возрастает на 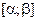 от
от 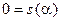 до
до 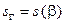 . Обратная функция
. Обратная функция 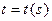 возрастает на
возрастает на 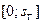 , множество ее значений есть
, множество ее значений есть 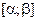 ;
; 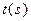 дифференцируема на
дифференцируема на 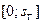 , причем
, причем 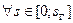
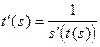 ( гл.2, п. 1.3.).
( гл.2, п. 1.3.).
Обозначим: 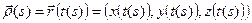 . Когда s возрастает от 0 до
. Когда s возрастает от 0 до 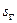 ,
, 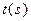 возрастает от a до b, так что годографом вектор- функции
возрастает от a до b, так что годографом вектор- функции 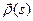 на
на 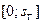 является годограф вектор-функции
является годограф вектор-функции 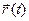 на
на 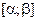 , т.е. кривая G. Следовательно, G можно задать параметрически уравнением
, т.е. кривая G. Следовательно, G можно задать параметрически уравнением
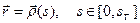 , (11)
, (11)
в котором параметр s имеет геометрический смысл длины дуги. Этот параметр называют натуральным параметром кривой G, а уравнение (11) – уравнением G с натуральным параметром (иногда – натуральным уравнением G).
Замечание. Вектор-функция 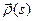 в уравнении (11) непрерывно дифференцируе- ма на
в уравнении (11) непрерывно дифференцируе- ма на 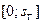 , причем
, причем 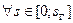
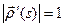 .
.
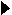 Из (2) следует, что
Из (2) следует, что 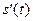 непрерывна и не обращается в нуль на
непрерывна и не обращается в нуль на 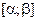 ; поэтому
; поэтому 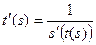 непрерывна на
непрерывна на 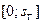 . Имеем:
. Имеем: 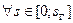
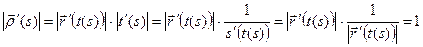 .
. 
