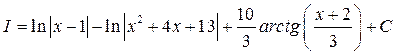Тема 1, 2. Раціональні дроби та їх інтегрування.
Означення 1. Дріб називається раціональним, якщо його чисельник та знаменник є многочленами, тобто дріб має вигляд
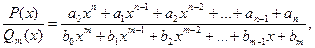
де аі та bk — коефіцієнти многочленів, і = 0, 1, ..., n;
k = 0, 1, 2, ..., m.
Раціональний дріб називається правильним, якщо найвищий показник степеня чисельника n менше відповідного степеня m знаменника. Дріб називається неправильним, якщо 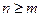 .
.
Якщо 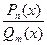 дріб неправильний, тоді треба поділити чисельник на знаменник (за правилом ділення многочленів) і одержати заданий дріб у вигляді суми многочлена та правильного раціонального дробу, тобто
дріб неправильний, тоді треба поділити чисельник на знаменник (за правилом ділення многочленів) і одержати заданий дріб у вигляді суми многочлена та правильного раціонального дробу, тобто
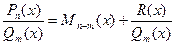
Означення 2. Найпростішими раціональними дробами І, II, III та IV типу називають правильні дроби вигляду:
I. 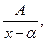 II.
II. 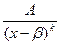
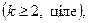
III. 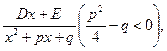
IV. 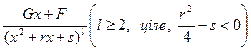
Умова 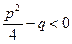 означає, що квадратний тричлен
означає, що квадратний тричлен 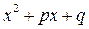 не має дійсних коренів і на множники не розкладається. Те саме можна сказати і про квадратний тричлен
не має дійсних коренів і на множники не розкладається. Те саме можна сказати і про квадратний тричлен 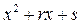 .
.
Розглянемо інтегрування найпростіших раціональних дробів. Інтеграли від найпростіших раціональних дробів 1-го та ІІ-го типів знаходять методом безпосереднього інтегрування:
І. 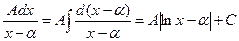
ІІ. 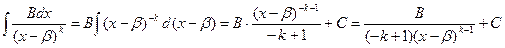
При інтегруванні найпростішого дробу ІІІ-го типу треба спочатку в знаменнику виділити повний квадрат, а потім той вираз, що під квадратом, замінити через нову змінну.
ІІІ. 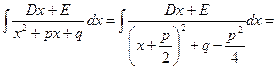
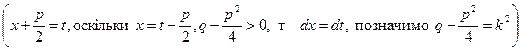
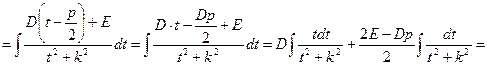
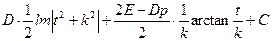
Повертаючись до змінної х, та враховуючи, що 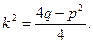 або
або 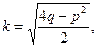 одержимо:
одержимо:
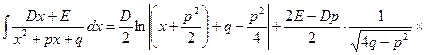
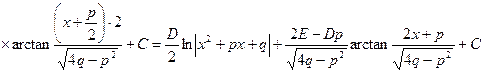
Інтеграл від найпростішого дробу типу IV шляхом повторного інтегрування частинами зводять до інтеграла під найпростішого дробу типу III.
Приклад. Обчислити інтеграл.
а) 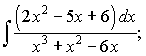 б)
б) 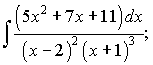 в)
в) 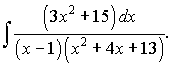
Розв'язок:
а) Оскільки степінь чисельника менший за степінь знаменника, то підінтегральна функція – правильний дріб. Знаменник
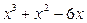 можна розкласти на множники
можна розкласти на множники 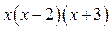 таким чином дріб розкладається на суму доданків першого типу (І):
таким чином дріб розкладається на суму доданків першого типу (І):
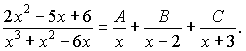
Невідомі коефіцієнти 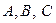 знаходимо методом невизначених коефіцієнтів. Для цього праву частину отриманої тільки що нерівності зводимо до спільного знаменника:
знаходимо методом невизначених коефіцієнтів. Для цього праву частину отриманої тільки що нерівності зводимо до спільного знаменника:
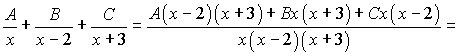
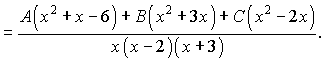
Прирівнюємо чисельники для знаходження невідомих коефіцієнтів
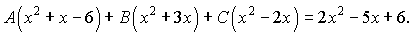
Ця рівність виконується коли коефіцієнти при однакових степенях 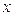 рівні між собою. З цієї у мови отримуємо систему лінійних рівнянь для визначення невідомих
рівні між собою. З цієї у мови отримуємо систему лінійних рівнянь для визначення невідомих 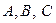
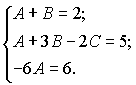
З цієї системи знаходимо невідомі
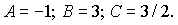
Наша підінтегральна функція набуде вигляду
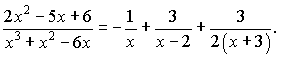
Інтегруючи останню рівність отримаємо
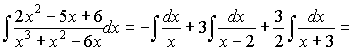
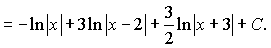
б) Підінтегральна функція
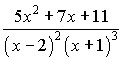
є правильним дробом, знаменник якого має дійсні корені. Такий дріб розкладається на суму найпростіших дробів І-го та ІІ-го типів
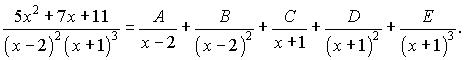
Визначимо невідомі коефіцієнти 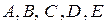 , для цього праву частину зведемо до спільного знаменника.
, для цього праву частину зведемо до спільного знаменника.
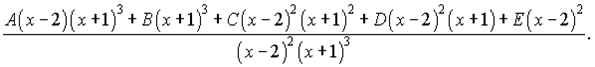
Розкриваємо дужки і прирівнюємо коефіцієнти при однакових степенях в чисельниках. Отримаємо наступну систему лінійних рівнянь
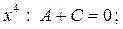
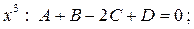
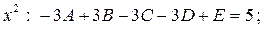
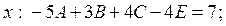
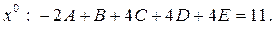
Є інший спосіб отримання системи рівнянь для визначення невідомих. Чисельники справа і зліва повинні бути рівні для всіх 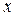 . Ця особливість дещо спрощує розв'язування системи рівнянь. Як правило, за точки
. Ця особливість дещо спрощує розв'язування системи рівнянь. Як правило, за точки 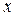 в першу чергу беруть корені рівняння та 0. В нашому випаду це були б значення
в першу чергу беруть корені рівняння та 0. В нашому випаду це були б значення 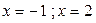 . Нуль вибирають за рахунок простоти обчислень.
. Нуль вибирають за рахунок простоти обчислень.
Розв'язавши отриману вище систему рівнянь, отримаємо наступні значення невідомих:
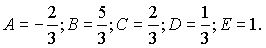
Інтегруємо підінтегральну функцію, врахувавши знайдені константи
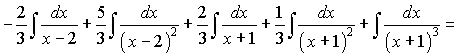
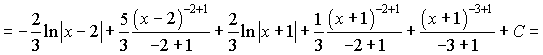
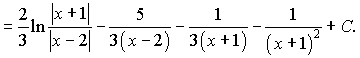
б) Підінтегральна функція є правильним дробом. Знаменник містить квадратний тричлен множники. Даний дріб за правилами розкладається на суму дробів І-го та ІІІ-го типів:
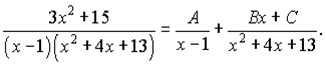
Звівши до спільного знаменника, матимемо:
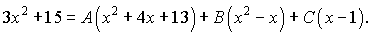
Можемо прирівняти коефіцієнти при однакових степенях, але поступимо інакше, щоб навчитися використовувати іншу методику. Тож підставимо корінь 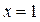 в ліву і праву частину рівності, отримаємо
в ліву і праву частину рівності, отримаємо
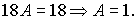
Щоб позбутися невідомої 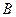 підставимо
підставимо 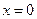
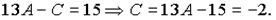
Для знаходження невідомої 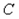 випишемо постійні при
випишемо постійні при 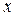
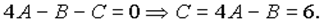
В такий спосіб, не виписуючи систем лінійних рівнянь і не розв'язуючи їх, можна досить швидко знайти невідомі.
Підставивши знайдені значення, отримаємо інтеграл
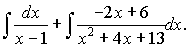
Перший доданок інтегруємо
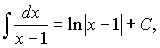
а до другого застосовуємо заміну
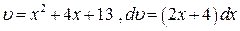
та зводимо до суми двох
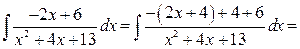
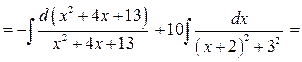
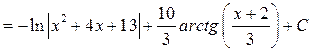
Підсумувавши отримані інтеграли, остаточно отримаємо розв'язок: