Линейные операции над векторами
ОГЛАВЛЕНИЕ
| ГЛАВА 1. ВЕКТОРНАЯ АЛГЕБРА ...................................................… §1. Основные определения и линейные операции ............................... §2. Линейная зависимость векторов .................................................….. §3. Разложение вектора на составляющие........................................….. §4. Векторный базис, координаты вектора.......................................….. §5. Скалярное произведение векторов..............................................….. §6. Векторное произведение векторов..............................................….. §7. Векторно-скалярное произведение трех векторов....................…... ГЛАВА 2. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.................................….. §1. Декартова прямоугольная система координат ...........................….. § 2. Простейшие задачи аналитической геометрии..........................….. §3. Важнейшие системы координат на плоскости и в пространстве ... §4. Уравнения линий и поверхностей ...............................................…. §5. Линейные образы на плоскости ...................................................…. §6. Взаимное расположение двух прямых ........................................…. §7. Определение расстояния от точки до прямой.............................…. §8. Пучок прямых на плоскости.........................................................…. §9. Линейные образы в пространстве.................................................…. §10. Взаимное расположение двух плоскостей.................................…. §11. Расстояние от точки до плоскости..............................................…. §12. Прямая линия в пространстве.....................................................…. §13. Взаимное расположение двух прямых.......................................…. §14. Расстояние между скрещивающимися прямыми......................…. §15. Прямая и плоскость в пространстве...........................................…. §16. Пучок плоскостей.........................................................................…. §17. Линии второго порядка на плоскости........................................….. §18. Поверхности второго порядка....................................................….. §19. Преобразование координат на плоскости.................................….. §20. Исследование уравнения второго порядка на плоскости........…. ГЛАВА 3. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ.......................... .….. §1. Числовые матрицы........................................................................…... §2. Определители...............................................................................…… §3. Миноры и алгебраические дополнения......................................….. §4. Разложение определителя по элементам строки или столбца…… §5. Квадратные матрицы..................................................................……. §6. Система n линейных уравнений с n неизвестными.................……. §7. Ранг матрицы...............................................................................……. §8. Система линейных алгебраических уравнений........................…… §9. Структура решения системы линейных уравнений.................…… §10. Линейные пространства............................................................…… §11. Линейные операции над векторами, заданными в произвольном базисе..................................................................………………………… §12. Линейные преобразования........................................................…… §13. Невырожденные линейные преобразования...........................…… §14. Евклидовы пространства...........................................................…… §15.Ортогональные матрицы...........................................................……. §16. Квадратичные формы................................................................…… §17. Аффинные пространства...........................................................…… §18. Евклидово точечно-векторное пространство. Приведение уравнений второго порядка к каноническому виду.................…………….. |
ГЛАВА 1
ВЕКТОРНАЯ АЛГЕБРА
§ 1 .ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ЛИНЕЙНЫЕ ОПЕРАЦИИ
ПОНЯТИЕ ВЕКТОРА
 A B A B
Рис.1. |
Вектором называется направленный отрезок 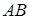 , где точка
, где точка 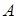 называется началом, точка
называется началом, точка 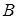 -
-  концом вектора. Обозначается вектор символом
концом вектора. Обозначается вектор символом 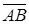 или
или  (рис.1). Длина отрезка называется модулем (длиной) вектора и обозначается символом
(рис.1). Длина отрезка называется модулем (длиной) вектора и обозначается символом 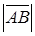 или
или 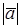 .
.
Векторы представляют математическую абстракцию физических векторных величин, которые характеризуются численным значением и направлением в пространстве. Таковы, например, перемещение, скорость, сила, напряженность магнитного поля, напряженность электрического поля. Векторы, как и физические векторные величины, делятся на три группы:
1) Свободные векторы, которые можно перемещать в пространстве параллельно самому себе; они характеризуются модулем и направлением; за начало свободного вектора можно принять любую точку пространства;
2) Скользящие векторы, которые можно перемещать по данной прямой, называемой линией действия вектора; они характеризуются модулем, направлением и линией действия; за начало скользящего вектора можно принять любую точку прямой, на которой он расположен;
3) Связанный (закрепленный) вектор, который характеризуется модулем, направлением и точкой, где расположено начало вектора.
Если особо не оговорено, то в дальнейшем под словом “вектор” подразумевается свободный вектор.
РАВЕНСТВО ВЕКТОРОВ
Векторы 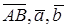 называются равными, если они имеют равные модули и одинаково направлены (рис. 2)
называются равными, если они имеют равные модули и одинаково направлены (рис. 2)
Равенство векторов записывается в виде 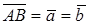 .
.
КОЛЛИНЕАРНЫЕ ВЕКТОРЫ
A B 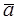 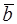 Рис. 2. Рис. 2. |
Векторы  и
и 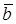 называются коллинеарными, если их направления совпадают или противоположны. Коллинеарность векторов
называются коллинеарными, если их направления совпадают или противоположны. Коллинеарность векторов  и
и 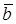 обозначается символом
обозначается символом  ||
|| 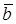 . Символы
. Символы 
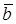 и
и  ¯
¯ 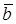 означают, что векторы
означают, что векторы  и
и 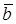 коллинеарны и соответственно одного и противоположного направления.
коллинеарны и соответственно одного и противоположного направления.
КОМПЛАНАРНЫЕ ВЕКТОРЫ
Векторы, параллельные одной плоскости, называются компланарными.
НУЛЬ - ВЕКТОР
Вектор, модуль которого равен нулю, называется нулевым (нуль-вектором) и обозначается символом `0.Направление нуль-вектора не определено.
ЕДИНИЧНЫЙ ВЕКТОР (ОРТ)
Вектор, модуль которого равен единице, называется единичным или ортом.
УГОЛ МЕЖДУ ВЕКТОРАМИ
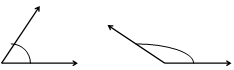 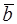 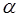 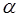 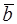 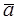 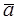 Рис. 3. Рис. 3. |
Углом между векторами  и
и 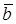 называется наименьший из двух углов между ними, проведенными из одной точки (приведенными к общему началу) (рис.3).
называется наименьший из двух углов между ними, проведенными из одной точки (приведенными к общему началу) (рис.3).
Из определения следует, что
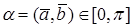
УГОЛ МЕЖДУ ВЕКТОРОМ И ОСЬЮ
Осью называется прямая с выбранным положительным направлением. Направление оси может быть определено при помощи какого-нибудь ненулевого вектора 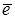 (рис.4). Углом между осью и вектором (рис.4). Углом между осью и вектором  называется угол называется угол 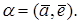 | 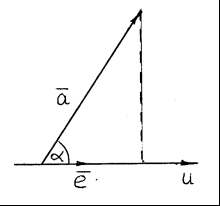 Рис. 4 Рис. 4 |
ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ
(НА НАПРАВЛЕНИЕ ДРУГОГО ВЕКТОРА)
Проекцией вектора  на ось
на ось 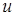 (на направление вектора
(на направление вектора 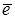 ) называется число
) называется число 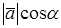 (рис.4) и обозначается символом
(рис.4) и обозначается символом 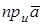 или
или 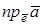 .
.
Замечание. Если вектор  - единичный, то
- единичный, то 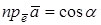 .
.
ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ
Линейными операциями над векторами называют операцию сложения векторов и операцию умножения вектора на вещественное число.
СЛОЖЕНИЕ ВЕКТОРОВ
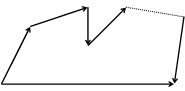 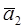 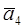 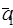 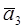 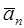 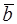 Рис. 5. Рис. 5. |
Пусть даны векторы 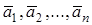 . Из данных векторов строим ломаную, выбирая за начало вектора
. Из данных векторов строим ломаную, выбирая за начало вектора 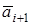 конец вектора
конец вектора 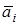 (рис.5).
(рис.5).
Определение. Суммой векторов 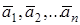 называется вектор
называется вектор 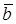 , который замыкает ломаную, построенную из данных векторов, причем начало вектора
, который замыкает ломаную, построенную из данных векторов, причем начало вектора 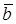 совпадает с началом первого слагаемого, конец - с концом последнего слагаемого (правило многоугольника).
совпадает с началом первого слагаемого, конец - с концом последнего слагаемого (правило многоугольника).
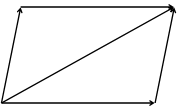 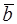 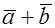 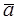  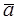 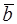 Рис. 6. Рис. 6. |
Обозначение суммы:
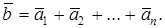
Из определения суммы следует правило параллелограмма для двух слагаемых (рис.6).
СВОЙСТВА ОПЕРАЦИИ СЛОЖЕНИЯ
1. 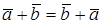 (коммутативность суммы)
(коммутативность суммы)
2. 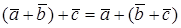 (ассоциативность суммы).
(ассоциативность суммы).
Доказательство свойств.
Первое свойство очевидно из рис.6. Для доказательства второго свойства строим ломаную из векторов 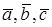 (рис.7). Из построения видно, что
(рис.7). Из построения видно, что 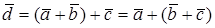 .
.
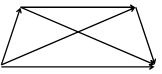 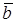  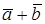  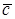 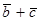  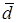 Рис. 7. Рис. 7. |
ВЫЧИТАНИЕ ВЕКТОРОВ
Разностью 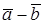 двух векторов называется третий вектор
двух векторов называется третий вектор 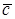 такой, что
такой, что 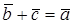 . Для построения вектора
. Для построения вектора 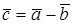 векторы
векторы  и
и 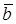 приводим к общему началу и по правилу многоугольника находим вектор
приводим к общему началу и по правилу многоугольника находим вектор 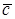 так, чтобы
так, чтобы 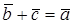 (рис. 8) .Получаем, что вектор
(рис. 8) .Получаем, что вектор 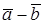 направлен от конца вычитаемого вектора к концу уменьшаемого вектора.
направлен от конца вычитаемого вектора к концу уменьшаемого вектора.
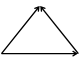 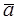 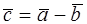 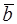 Рис. 8. Рис. 8. | 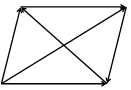 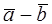 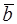 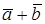  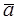 Рис. 9. Рис. 9. |
Замечание. Векторы 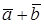 и
и 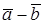 служат диагоналями параллелограмма, построенного на векторах
служат диагоналями параллелограмма, построенного на векторах  и
и 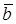 (рис.9)
(рис.9)
УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО (СКАЛЯР)
Пусть даны вектор  и скаляр
и скаляр 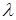 . Тогда
. Тогда 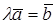 , где
, где 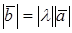 и
и 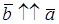 при
при 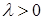 ,
, 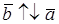 при
при 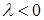 .
.


