Модельный пример

Приведена зависимость напряжённости электростатического поля (y) в процессе гидромониторной промывки ёмкости после нефтепродукта от диэлектрической проницаемости моющей жидкости (x). Результаты эксперимента представлены в таблице 2.1.

Таблица 2.1 – Результаты эксперимента

№ п/п	X	Y	№ п/п	X	Y	№ п/п	X	Y
								71,5
							63,5
	52,5	31,5
							64,5
	54,5				68,5

Построим эмпирическую линию регрессии, чтобы определить вид уравнения.

Для этого разобьем рассматриваемый диапазон значений x на n равных интервалов. Для определения n числа интервалов воспользуемся формулой Стерджеса:

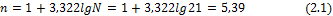
Округляем полученный результат до 5.

Ширина интервала h будет равна

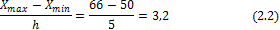
Таким образом получим следующие границы и частные средние значения интервалов (таблица 2.2).

Таблица 2.2 – Границы и частные средние значения интервалов

Интервал	Границы интервала	Частные средние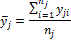
	[50;53,2]	31,5
	(53,2;56,4]	44,25
	(56,4;59,6]
	(59,6;62,8]	69,8
	(62,8;66]	74,25

Соединим полученные точки отрезками прямой (рисунок 2.1).

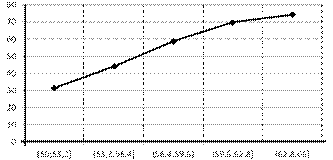
Рисунок 2.1 – Эмпирическая линия регрессии

Исходя из полученного графика, можно предположить, что данная зависимость имеет линейный, либо степенной вид. Соответственно, необходимо найти коэффициенты для двух уравнений регресси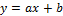и: и .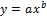

Линейное уравнение .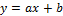

Коэффициенты линейного уравнения определяются по формулам (1.10) и (1.11.)

Промежуточные расчёты представлены в таблице 2.3

Таблица 2.3 – Промежуточные расчёты

Величина	Значение
∑Х
∑У	1166,5
∑Х2
∑ХУ	69589,25
(∑Х)2

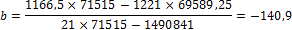
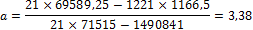
Степенное уравнение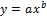

Коэффициенты данного уравнения будут определяться по формуле (1.14). a=22,296; b=0,3954.

Проверим среднюю погрешность аппроксимации 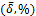для каждого из построенных уравнений регрессии. Расчёт проводится по формуле (1.19).

;

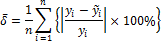
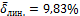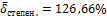
Исходя из значений средней погрешности аппроксимации можно сделать вывод, что уравнение регрессии линейного вида точнее описывает эмпирическую зависимость.