Лекция 20 Исследование функции и построение ее графика
ИКТИБ ИТА ЮФУ
КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ
Лекция 20 Исследование функции и построение ее графика
План лекции
Остаточный член в формуле Тейлора. Условия монотонности функции. Экстремумы функции. Необходимое и достаточные условия экстремума функции. Наибольшее и наименьшее значения функции, дифференцируемой на заданном отрезке. Направления выпуклости и точки перегиба графика функции. Асимптоты графика функции. Общая схема исследования функции и построения её графика.
Напомним важнейшие разложения функций по формуле Тейлора (Маклорена) из прошлой лекции:
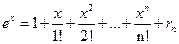 , (7)
, (7) 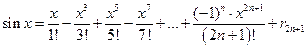 , (8)
, (8)
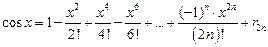 , (9)
, (9) 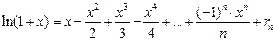 . (12)
. (12)
Формула (9) может быть получена непосредственно и из формулы (8) дифференцированием ее левой и правой частей.
И это не случайно. Не обязательно каждый раз вычислять все производные исследуемой функции.
Пример 1(6). Напишите формулу Тейлора для функции 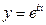 в точке
в точке 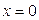 (формулу Маклорена для функции
(формулу Маклорена для функции 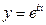 ).
).
Решение. Искомую формулу мы получим, заменив в формуле (7) аргумент 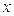 на аргумент
на аргумент 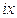 . Учитывая, что
. Учитывая, что 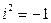 , мы приходим к искомой формуле
, мы приходим к искомой формуле 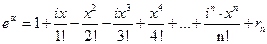 . (10)
. (10)
Сопоставляя формулы (7), (8), (9), (10), мы приходим к формуле Эйлера 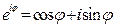 , (11) которая упоминалась в лекции 1. Полностью формула Эйлера будет доказана, когда будет установлено, что в формулах (7), (8), (9) остаточные члены с ростом
, (11) которая упоминалась в лекции 1. Полностью формула Эйлера будет доказана, когда будет установлено, что в формулах (7), (8), (9) остаточные члены с ростом 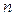 стремятся к 0 при всех значениях аргумента.
стремятся к 0 при всех значениях аргумента.
Пример 2(7). Напишите формулу Тейлора для функции 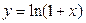 в точке
в точке 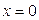 (формулу Маклорена для функции
(формулу Маклорена для функции 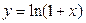 ).
).
Решение. Если 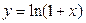 , то
, то 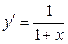 ,
, 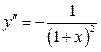 ,
, 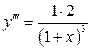 ,
, 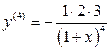 , …,
, …, 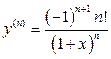 (
( 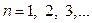 ). Следовательно, искомая формула принимает вид
). Следовательно, искомая формула принимает вид 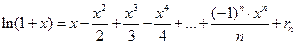 . (12)
. (12)
Неотъемлемой частью использования формулы Тейлора является оценка ее остаточного члена. Красивые и практичные формулы появлялись в работах выдающихся математиков 18, 19 и да в 20 веках. Отметим некоторые результаты без доказательства.
Теорема 1(5). (Теорема Лагранжа) Пусть функция 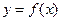 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 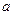 производную
производную 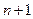 -го порядка. Тогда для произвольной точки
-го порядка. Тогда для произвольной точки 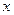 из этой окрестности найдется точка
из этой окрестности найдется точка 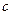 , принадлежащая интервалу, соединяющую точки
, принадлежащая интервалу, соединяющую точки 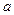 и
и 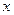 , обладающую тем свойством, что в формуле (5) выполнено соотношение
, обладающую тем свойством, что в формуле (5) выполнено соотношение 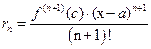 , (13)
, (13)
Теорема 2(6). (Теорема Коши) Пусть функция 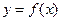 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 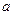 производную
производную 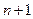 -го порядка. Тогда для произвольной точки
-го порядка. Тогда для произвольной точки 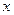 из этой окрестности найдется точка
из этой окрестности найдется точка 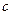 , принадлежащая интервалу, соединяющую точки
, принадлежащая интервалу, соединяющую точки 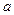 и
и 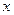 , обладающую тем свойством, что в формуле (5) выполнено соотношение
, обладающую тем свойством, что в формуле (5) выполнено соотношение 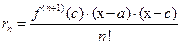 , (14)
, (14)
Теорема 3(5). (Теорема Пеано) Пусть функция 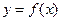 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки 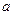 производную
производную 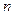 -го порядка. Тогда в формуле (5) выполнено соотношение
-го порядка. Тогда в формуле (5) выполнено соотношение 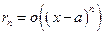 , (15)
, (15)
Так как производные функции 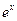 равны между собой и ограничены на любом фиксированном отрезке
равны между собой и ограничены на любом фиксированном отрезке 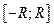 , то остаточный член
, то остаточный член 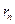 в формуле
в формуле 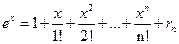 стремится к нулю при
стремится к нулю при 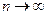 для каждого фиксированного
для каждого фиксированного 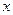 .
.
Тем более то же самое справедливо для функций 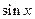 и
и 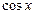 , так как производные этих функций не превосходят по модулю 1. В формулах
, так как производные этих функций не превосходят по модулю 1. В формулах 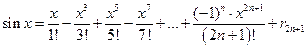 и
и 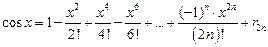 остаточный член стремится к нулю при
остаточный член стремится к нулю при 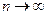 для каждого
для каждого 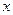 .
.
Можно доказать, что в формуле 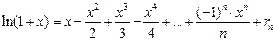 остаточный член стремится к нулю при
остаточный член стремится к нулю при 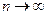 для каждого
для каждого 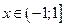 . Посмотрите, как выглядит эта формула при
. Посмотрите, как выглядит эта формула при 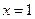 .
.
