В. 3. Бесконечно малые величины

ЧОУ ВПО Институт экономики управления и права (г.Казань)

Экономико-правовой колледж

Курс лекций по дисциплине «Математика»

Для студентов заочного отделения на базе среднего полного(основного) образования

.

Разработал преподаватель

Парышева Е.П.

Казань 2011

Тема 1. Пределы и непрерывность

В.1. Предел числовой последовательности

Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число a_n, то говорят, что задана числовая последовательность {a_n}:

a₁, a₂,…,a_n… .

Другими словами, числовая последовательность – это функция натурального аргумента a_n=f(n).

Числа a₁, a₂,…,a_n называются членами последовательности, а число a_n– общим или n-м членом данной последовательности.

Пример 1: а) 2, 4, 6, …2n, … (монотонная неограниченная);

б) 1, 0, 1, 0, … (немонотонная ограниченная);

в) 0, 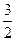, , 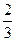, , 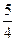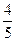…, , … 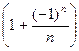- немонотонная, ограниченная. Изобразим её точками числовой оси. С ростом n последовательность как угодно близко приближается к 1. При этом 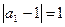, , 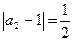, 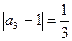… , , … 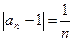Т.е. с ростом n расстояние 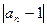будет меньше любого, сколь угодно малого числа.

Число А называется пределом числовой последовательности {a_n}, если для любого сколь угодно малого положительного числа e > 0 найдется такой номер N(e), зависящий от e, что для всех членов данной последовательности с номерами n > N(e) верно неравенство |a_n - A| < e .

Предел числовой последовательности обозначается 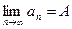или 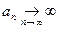. Используя следующие логические символы (кванторы): " (любой), $ (существует), Û (равносильность или эквивалентность), определение предела можно записать в виде:

(A = 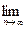a_n)Û ("e > 0 $ N(e) : "n > N(e) | a_n – A | < e)

Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.

Смысл определения: для достаточно больших n члены последовательности {a_n} сколь угодно мало отличаются от числа А.

В.2. Предел функции

Число А называется пределом функции y = f(x) при х, стремящемся к бесконечности (пределом функции в бесконечности), если для любого e > 0 найдется такое S > 0, что для всех |х| > S верно неравенство | f(x) – A | < e.

Предел функции обозначается 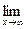f(x) = A, или f(x) ® A при х ® ¥ ( ).

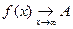(A = 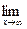f(x) Û ("e > 0 $ S = S(e) > 0 : "x : | x | > S | f(x) – A | < e).

Смысл определения: при достаточно больших по модулю значениях х значения функции f(x) как угодно мало отличаются от числа А.

Число А называется пределом функции f(x) при х ® х₀, (в точке х₀), если для

"e > 0 $ d = d(e) > 0 : "x ¹ x_0, |х – x₀| < d выполняется неравенство | f(x) – A | < e.

Смысл определения: для всех значений х, достаточно близких к х₀, значения f(x) как угодно мало отличаются от числа А.

Замечание 1. Определение предела не требует существования функции в самой точке х₀, поскольку предполагается, что х стремится к х₀, но не достигает значения х₀. Поэтому наличие или отсутствие предела при х ® х₀ определяется поведением функции в окрестности точки х₀, но не связано с существованием функции в самой точке х₀.

Замечание 2. Если при х ® х₀ х принимает только значения, меньшие х₀, и при этом функция f(x) стремится к некоторому числу А, то говорят об одностороннем пределе функции слева: 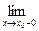f(x) = A.

Аналогично, если при х ® х₀ х > х₀, то говорят об одностороннем пределе функции справа, т.е: 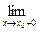f(x) = A

При этом, если 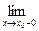f(x) = 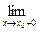f(x) = А, то 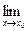f(x) = A.

В. 3. Бесконечно малые величины

Функция a(x) называется бесконечно малой величиной при х ® х₀(при х ® ¥), если ее предел равен нулю: 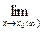a(x) = 0.

Например, функция 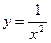- б.м.в. при х ® ¥, 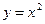- б.м.в. при х ®0.

Связь бесконечно малых величин с пределами функций определяется теоремами:

Теорема: Если 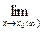f(x) = A, то функцию f(x) можно представить в виде суммы

f(x) = A + a(x), где a(x) – бесконечно малая при х ® х₀ (¥).

Обратная теорема: Если функцию f(x) можно представить как сумму числа А и бесконечно малой a(x) при х ® х₀ (¥), то число А есть предел этой функции при х ® х₀ (¥), т.е.

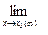f(x) = A.

Свойства бесконечно малых величин:

1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.

2. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая.

3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Замечание. Свойство 3 не рассматривает предел отношения двух бесконечно малых a(x) и b(x) из-за его неопределенности. Этот предел 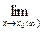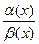может быть равен нулю, числу А ¹ 0 или бесконечности ¥. При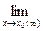 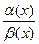=1 a(x) и b(x) называются эквивалентными и пишут a(x) »b(x).