Закон сохранения момента импульса

Если рассматривать движение не одной материальной точки, а системы материальных точек, то окажется, что в уравнении моментов нужно учитывать только моменты внешних сил. Моменты сил взаимодействия частей системы на результат не влияют. И для системы материальных точек (и для твердого тела) уравнение моментов примет вид:

.

Здесь под надо понимать суммарный момент импульса системы: , где - момент импульса отдельной материальной точки, а в правой части стоит сумма моментов внешних сил: .

Из данного уравнения следует, что

при равенстве нулю суммарного момента внешних сил суммарный момент импульса тела (или системы тел) остается постоянным.

Это утверждение и является законом сохранения момента импульса (ЗСМИ). Так же, как и закон сохранения импульса (ЗСИ), ЗСМИ должен выполняться в замкнутой системе. Но кроме этого возможна ситуация, когда тело находится в поле внешней силы (система незамкнута), а момент этой силы равен нулю. Такие силы называются центрально симметричными или просто центральными. Математически такая сила может быть представлена в виде: . Нетрудно видеть, что векторное произведение такой силы на радиус вектор равен нулю.

Таким образом ЗСМИ выполняется в замкнутой системе и в поле центральных сил.

Примеры центральных сил: сила гравитационного притяжения планет Солнцем, сила кулоновского взаимодействия ядра и электронов в атоме.

Особенности описания движения твердого тила

При движении твердого тела необходимо учитывать как перемещение тела в пространстве в целом, так и поворот его вокруг оси, проходящей через центр масс. Для анализа движения твердого тела его мысленно разбивают на множество материальных точек. Скорость каждой из них может быть представлена как сумма двух скоростей: , где - скорость отдельной (i-той) точки, - скорость центра масс твердого тела, а - скорость этой точки относительно центра масс. Проанализировав движение отдельной точки, пользуясь выводами динамики материальной точки, можно затем результат просуммировать (или проинтегрировать) для тела в целом. При этом удобнее применять именно операцию интегрирования, для чего отдельные части (точки) тела принимаются бесконечно малыми.

Движение центра масс

Согласно второму закону Ньютона для отдельно взятой элементарной массы, которую считаем материальной точкой, с учетом внешних сил и сил взаимодействия между отдельными массами этого тела можно записать:

Просуммировав получим равенство:

Учитывая, что согласно третьему закону Ньютона 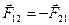, 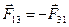и так далее, получим, что сумма сил взаимодействия окажется равной нулю и в данном равенстве останутся только внешние силы:

Учтем, что положение центра масс определяется по формуле.: , тогда: . Дважды продифференцировав это равенство получим:

.

А это значит, что основное уравнение динамики (II закон Ньютона), для центра масс записывается так же, как и для материальной точки, но с учетом только внешних сил (для материальной точки все силы внешние):

.

Здесь - равнодействующая внешних сил, а - масса всего твердого тела.

Ускорение центра масс твердого тела, умноженное на полную массу тела, равняется равнодействующей внешних сил, действующих на тело.