Температурное поле и коэффициент эффективности ребра постоянного поперечного сечения

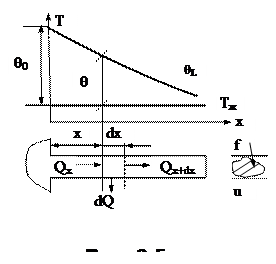
Рассмотрим на рис. 3.5 ребро постоянного поперечного сечения, для которого изменением температуры по поперечному сечению ребра можно пренебречь по сравнению с изменениями температуры по длине ребра.

Рис. 3.5

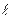Коэффициент теплоотдачи a и температура окружающей среды Т_ж постоянны для всей поверхности ребра. Площадь поперечного сечения ребра f, периметр сечения u, длина ребра и коэффициент теплопроводности материала l также постоянны. При стационарном тепловом режиме поток тепла Q_x, подводимый в сечении ребра х частично теплопроводностью передается вдоль ребра Q_x+dx частично рассеивается в окружающую среду dQ.

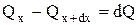. (а)

Вводя избыточную температуру J=T-T_ж, согласно закону Фурье имеем

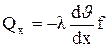(б)

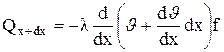(в)

Но по закону Ньютона-Рихмана

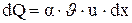. (г)

Подставив соотношения (б), (в) и (г) в формулу (а), получим

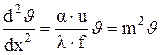, (3.67)

где .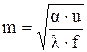

Решением дифференциального уравнения (3.67) является функция

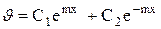. (3.68)

Константы интегрирования С₁ и С₂ можно определить из граничных условий:

при х=0; J=J₀,

x=l; ,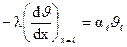

где J_l, 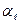– избыточная температура и коэффициент теплоотдачи на торце ребра.

На торце ребра избыточная температура минимальна, и поверхность его часто меньше боковой поверхности ребра. Поэтому теплообменом с торца ребра часто можно пренебречь. В этом случае второе граничное условие запишется в виде

при x=l;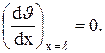

Определим константы интегрирования, пренебрегая теплоотдачей с торца ребра. Подстановка граничных условий в уравнение (3.68) дает

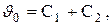
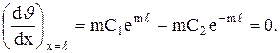
Из совместного решения этих уравнений определяются С₁ и С₂

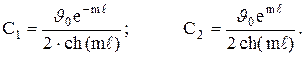
Гиперболический косинус выражается формулой

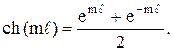
Подставив С₁ и С₂ в формулу (3.68), получим уравнение для температурного поля в ребре

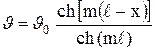. (3.69)

Избыточная температура на конце ребра при x = 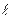равна

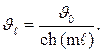
Весь рассеиваемый ребром поток тепла проходит путем теплопроводности через сечение его основания. Поэтому

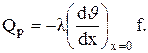
Продифференцировав (3.69) и подставив в эту формулу, получим

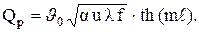(3.70)

Эта формула не учитывает теплоотдачу торца ребра. Если принять, что коэффициент теплоотдачи на торце ребра такой же, как на его боковой поверхности, то теплоотдачу торца ребра можно учесть удлинением ребра на величину f/u и вместо длины ребра l в расчетах использовать эффективную длину l_эф=l+f/u. Тогда коэффициент эффективности ребра постоянного по длине произвольного поперечного сечения равен

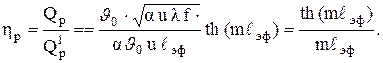(3.71)

Нестационарная теплопроводность

Общие положения

При нестационарном процессе теплопроводности или теплопередачи температура в каждой точке тела изменяется во времени. Если при стационарном режиме поток тепла, подводимый к телу, равен потоку тепла отводимому от тела, то при нестационарном режиме переноса тепла эти потоки не равны. Разность этих потоков тепла в соответствии с законом сохранения энергии расходуется на изменение энтальпии тела, что связано с изменением температуры во времени. Поэтому, в отличие от задач стационарной теплопроводности или теплопередачи, при решении уравнений (3.1) или (3.2) задают еще и начальные условия. Т.е. для того чтобы рассчитать, каким будет температурное поле в теле для некоторого момента времени, необходимо задать, каким оно было в некоторый начальный момент времени.

Однако для тел конечных размеров в случае постоянных, не зависимых от времени граничных условий, протекание процесса нестационарной теплопро-водности можно подразделить на две стадии. В первые моменты процесса характер изменения температуры различных точек тела во времени будет различным. Температура поверхности тела с начала процесса начнет приближаться к температуре окружающей среды, тогда как участки тела, удаленные от поверхности, могут некоторое время сохранять свою температуру или изменять ее в зависимости от начального распределения температур. Эта стадия процесса называется неупорядоченной. По истечении некоторого промежутка времени начальное распределение температур перестает влиять на характер протекания процесса. Закон изменения температуры во времени становится одинаковым для всех точек тела. Эту стадию процесса называют регулярным режимом.

При периодических во времени граничных условиях протекание процесса нестационарной теплопроводности также можно подразделить на две стадии. В стадии неупорядоченного режима температурное поле в теле зависит от начального распределения температур. По истечении некоторого промежутка времени в теле устанавливается квазистационарное температурное поле. Оно характеризуется тем, что в любой точке тела температура изменяется во времени, но ровно через период температура в любой точке тела принимает тоже значение.

Для определения температурного поля в телах классической формы (плоская неограниченная по длине и ширине стенка, неограниченный цилиндр, шар) используют аналитические методы решения. В телах сложной формы температурное поле определяют в результате численного интегрирования уравнений (3.1) и (3.2).