Определение реакций в кинематических парах структурной группы (2.3)

Силовой расчет механизма

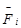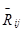Необходимо определить внешние силы на звеньях механизма ,реакции в кинематических парах и . Внешнюю уравновешивающую нагрузку на входном звене 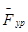и .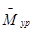

Расчёт проводится графическим планом сил и аналитически , с помощью вычисленных 13 положений.

Силовой расчет графоаналитическим методом планов

Силовой расчет графоаналитическим методом планов заключается в графоаналитическом решении векторных уравнений равновесия звеньев и структурных групп путем построения планов сил.

Внешние силы на звеньях

Движущая внешняя сила на поршне 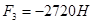направление по или против вектора .

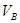Вертикальные силы веса

;

;

.

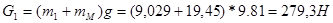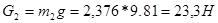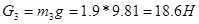Инерционные нагрузки звеньев:

- поршня 3 при поступательном движении сводится к вектору 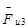сил инерции

,

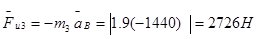- шатуна 2 при плоскопараллельном движении сводится инерционные нагрузки к вектору 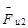и к моменту 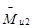сил инерции.

,

,

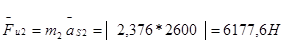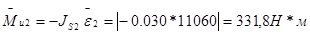- кривошипа 1 при неравномерном вращении 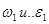сводится к вектору 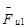и моменту сил инерции .

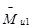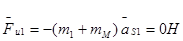, так как ,

.

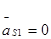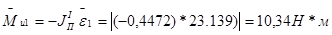Векторы 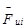направлены противоположно векторам 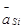центров масс, а моменты 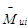противоположно ускорениям 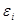(поз. 4 листа 2).

Определение реакций в кинематических парах структурной группы (2.3)

Поскольку силовой расчет ведется по группам Ассура, в порядке обратном их присоединения в механизме, то отделяем структурную группу из звеньев(2,3) и показываем ее в масштабе 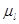в позиции 4 листа 2.

Кроме внешних сил 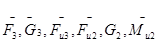, в точках отделениях группы от механизма показываем реакции 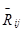:- 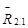во вращающейся кинематической паре А, известной точкой приложения (в центре А), но неизвестной по величине и направлению,

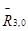- в поступательной кинематической паре В, известную направлением ( 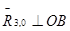) и неизвестная по величине и точкой приложения.

,

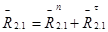где

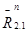- нормальная составляющая реакции, ,

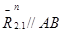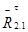- тангенциальная составляющая реакции, .

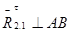Отрезки плеч 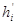относительно точки В в позиции 4.

Сумма моментов относительно точки В сил звена 2:

.

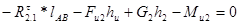Отсюда тангенциальная составляющая реакции равна

,

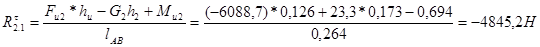где

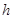- плечи сил относительно точки В, м.

,

.

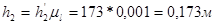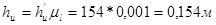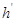- отрезки плеч в позиции 4 листа 2.

,

.

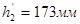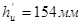Векторное уравнение равновесия сил группы (2,3).

,

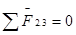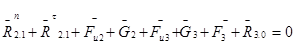. (4.1)

Решаем векторное уравнение графическим построением плана сил группы в позиции 5.

Для этого рассчитываем отрезки сил

.

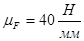(1 - 2) ,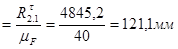

(2 - 3) ,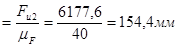

(3 - 4) ,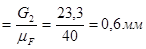

(4 - 5) ,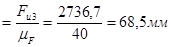

(5 - 6) ,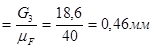

(6 - 7) . ?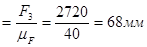

Откладываем в позиции 5 плана сил параллельно соответствующим векторам. Из последней точки 7 плана сил проводим 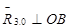, а из начальной точки 1 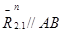. На пересечении этих направляющих в точке 8 план сил замыкается и отрезок (7 – 8) изображает в масштабе 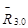. Отрезок (8 - 1) изображает в масштабе 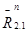. Из плана сил определяем крайние реакции ,

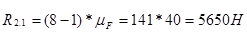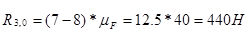
Внутреннюю реакцию 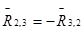определяем из уравнения равновесия сил одного звена например звена 2.

.

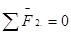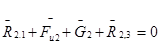. (4.2)

Поскольку 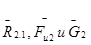уже отложены на плане, то достаточно соединить точки 4 и 8.

Тогда 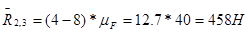.