Задача а рпр. расчёт статически определимого вала на прочность и жёсткость.
Задаётся: схема нагружения вала (рис.1, а), длины участков вала: l1= 2l; l2=2l; l3= l; l4= l; l5= 2l, размеры наружных диаметров: D1= 2d; D2= 2d; D3= 3d; D4= 3d; D5= 2d, размеры внутренних диаметров: d1= 1,5d; d2=d3=d4= 0; d5= d, величины распределённых моментов: m1= -4m; m2= 5m; m3= 0; m4= 0; m5= -2m, величины сосредоточённых моментов: М1= 2М; M2= -6M; M3= 4M; M4= -10M; M5= 8M; m=200нм/м; l= 0,5м; M= ml; G = 0,8×105МПа; [t] = 80МПа; [Q] = 0,25град/м. При расчетах учитывать соотношения: 1МПа=106Па=1Н/мм2=106Н/м2.
Требуется: 1) построить эпюры крутящих моментов Мк, касательных напряжений tmax и углов закручивания j; 2) из условия прочности и условия жёсткости определить размеры поперечных сечений вала.
      |

 2M 6M 4M 10M 8M
2M 6M 4M 10M 8M
 |  |  |  |  | |||||||
 | |||||||||||

 4m 5m 2m
4m 5m 2m





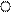






















 | |||
 | |||


 а)
а) 


 z
z

 |
























 |  |  | |||||||||
 |  | ||||||||||
 | |||||||||||
|






 2l 2l l l 2l
2l 2l l l 2l 





 400 эп. Мк
400 эп. Мк








 MK, 400 800
MK, 400 800







 Н×м 200
Н×м 200




















 б) z
б) z
 |  | ||

 200
200


 400
400
 800 600
800 600

 эп.
эп.  5,84
5,84

















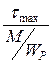 4,0 2,92
4,0 2,92



 в) 1,37 z
в) 1,37 z
 |






 0,51 1,22
0,51 1,22
 4,0
4,0
 5,48 2,640
5,48 2,640





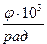 0,4l эп.j
0,4l эп.j



 г) 0,2044 z
г) 0,2044 z


































 l 1,495 3,066
l 1,495 3,066
 3,298 3,904
3,298 3,904
Рис. 1. Расчетная схема вала, эпюры крутящих моментов, касательных напряжений и углов закручивания
Решение
1. Определение реактивного момента МR в заделке (рис.1,а). Для определения реактивного момента составляется уравнение равновесия вала
åMz= MR+4m×2l-2m-5m×2l+6M-4M+10M+2m×2l -8M= 0.
Учитывая, что М= ml, определяется реактивный момент MR= -8ml+2M+10ml-6M+4M-10M-4ml+8m= -4M=-4×200 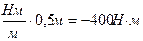 .
.
2. Разбивка вала на участки.
Для построения эпюры крутящих моментов Мк по длине вала необходимо рассмотреть пять участков с координатами: Z1, Z2, Z3, Z4, Z5 (рис.1,а).
3. Определение законов изменения крутящего момента по участкам вала.
3.1. Первый участок (рис.2)




 4m MK1
4m MK1




 | |||||
 | |||||
 |



 z
z

 |








 MR
MR 

Рис. 2. К определению Мк1 на первом участке
Координата z1 для первого участка изменяется в пределах 0 £ Z1 £ 2l. Уравнение равновесия для отсечённой (левой) части вала имеет вид
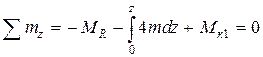 ; Mк1=MR+
; Mк1=MR+ 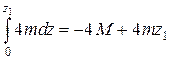 .
.
Крутящий момент на границах участка принимает значения: при z1= 0 MК1= -4М=-400Н×м, при z1= 2l MК1= -4М+8М= 4М=400Н×м.
3.2. Второй участок (рис.3)
2M





 4m 5m MK2
4m 5m MK2
 | |||
 |
z










 MR
MR






 2l z2
2l z2
Рис. 3. К определению МК2 на втором участке
На втором участке координата z2 изменяется в пределах 0 £ Z2 £ 2l. Уравнение равновесия для отсечённой части вала записывается в виде
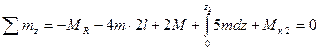 ,
, 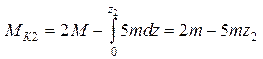 .
.
Крутящий момент на границах участка принимает значения:
при z2=0 МК2= 2M=200Н×м, при z2= 2lMК2= -8М=-800Н×м.
3.3. Третий участок (рис. 4)
6M MK3




 2M
2M






 4m 5m
4m 5m
 |

 z
z
 |







 MR 2l 2l z3
MR 2l 2l z3
 |
Рис. 4. К определению МК3 на третьем участке
Координата z3 для третьего участка изменяется в пределах 0 £ Z3 £ l. Уравнение равновесия отсечённой части вала и значения крутящего момента в граничных сечениях участка соответственно равны:
Smz= -MR-4m×2l+2M+5m×2l-6M+MК3= 0, МК3= -2М=-200Н×м.
На третьем участке крутящий момент постоянен по длине участка и равен МК3= -2М=-200Н×м.
3.4. Четвёртый участок (рис. 5).
На четвёртом участке координата z4 изменяется в пределах 0 £ Z4 £ l. Уравнение равновесия для отсечённой части вала записывается в виде
Smz= -MR-4m×2l+2m+5m×2l-6M+4M+MК4= 0, МК4= -6М=-600Н×м.
На четвёртом участке крутящий момент постоянен по длине участка и равен МК4= -6М=-600Н×м.
6M 4M MK4







 2M
2M
 |  | ||||||
 |  | ||||||






 4m 5m
4m 5m
 |

 z
z
 | |||
 |










 MR
MR
 | ||||||||
 | ||||||||
 | ||||||||
 |  | |||||||
2l 2l l z4
 |
Рис.5. К определению МК4 на четвёртом участке
3.5. Пятый участок (рис. 6)


 6M 4M 10M
6M 4M 10M









 2M MK5
2M MK5



 4m 5m 2m
4m 5m 2m




 z
z
 | ||||
 | ||||
 | ||||





 MR
MR
 |  | ||||||||||||
 |  |  |  | ||||||||||
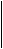 | |||||||||||||


 2l 2l l l z5
2l 2l l l z5
 |
Рис. 6. К определению МК5 на пятом участке
Координата z5 на пятом участке изменяется в пределах 0 £ Z5 £ 2l. Уравнение равновесия для отсечённой части вала имеет вид
Smz = -MR-4m×2l-2m-5m×2l-6M+4M-10M- 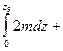 MК5= 0;
MК5= 0;
MК5= 4М+2mZ5.
Крутящий момент на границах пятого участка принимает значения:
при z5=0 MК5= 4M=400Н×м; при z5= 2l MК5= 8М=800Н×м.
По результатам вычислений строится эпюра крутящих моментов МК (рис.1, б)
4. Определение закона изменения касательного напряжения по участкам вала.
Для определения касательного напряжения по участкам вала пред-варительно вычисляются полярные моменты сопротивления сечений:
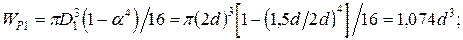
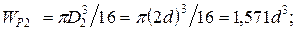
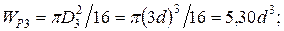
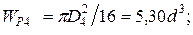
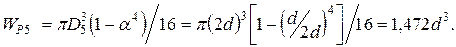
Затем наименьшее значение полярного момента сопротивления (в данном примере 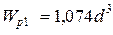 ) принимается за
) принимается за 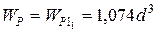 и определяют-ся значения полярных моментов сопротивления поперечных сечений вала пропорционально
и определяют-ся значения полярных моментов сопротивления поперечных сечений вала пропорционально 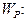
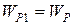 ;
; 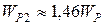 ;
; 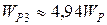 ;
; 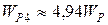 ;
; 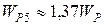 .
.
4.1. На первом участке закон изменения касательного напряжения в соответствии с формулой (3) имеет вид:
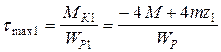 .
.
Касательное напряжение линейно зависит от координаты Z1 и на границах участка принимает значения:
при z1= 0 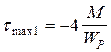 ; при z1= 2l
; при z1= 2l 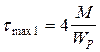 .
.
4.2. На втором участке касательное напряжение на границах участка принимает значения:
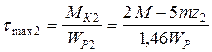 ;
;
при z2 = 0 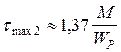 ; при z2 = 2l
; при z2 = 2l 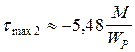 .
.
4.3. На третьем участке касательное напряжение равно:
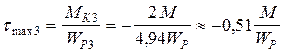 .
.
4.4. Касательное напряжение на четвертом участке равно:
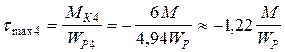 .
.
4.5. На пятом участке касательное напряжение линейно зависит от координаты z5 и на границах участка принимает значения:
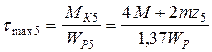 ;
;
при z5 = 0 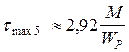 ; при z5= 2l
; при z5= 2l 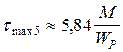 .
.
По результатам вычислений строится эпюра касательных напряжений tmax (рис. 1, в).
5. Определение размеров поперечных сечений вала из условия проч-ности.
Опасным является сечение, в котором действует наибольшее максимальное касательное напряжение.
Следовательно условие прочности запишется: max 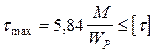 . Из условия прочности определяется диаметр вала в опасном сечении:
. Из условия прочности определяется диаметр вала в опасном сечении:
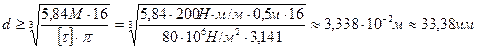 .
.
6. Определение размеров поперечных сечений вала из условия
жесткости. Условие жесткости записывается для сечения, где действует наибольший крутящий момент (рис. 1,б), при наименьших соотношениях размеров поперечного сечения вала. Для рассматриваемого примера условие жесткости записывается для крайнего правого сечения вала (на 5 участке).
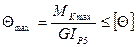
где 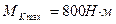 ,
, 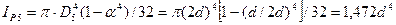
Из условия жесткости определяется диаметр вала:
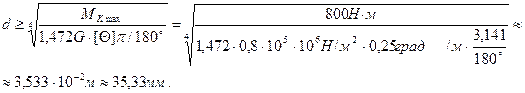
Анализируя значения диаметра вала, полученные из условия прочности и условия жесткости, окончательно принимаем 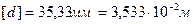 . Соответственно, размеры сечений вала по участкам равны:
. Соответственно, размеры сечений вала по участкам равны: 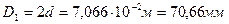 ;
; 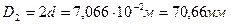 ;
; 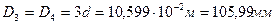 ;
; 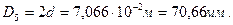
7. Определение закона изменения углов закручивания на участках вала.
Для определения углов закручивания по участкам вала пред-варительно вычисляются полярные моменты инерции сечений:
IP1= pD14(1-a4)/32 = p(2d)4[1-(1,5d/2d)4]/32= 1,074d4;
IP2= pD24/32 = p(2d)4/32 = 1,571d4;
IP3=pD34/32 = p(3d)4/32 = 7,951d4;
IP4=pD44/32 = p(3d)4/32 = 7,951d4;
IP5= pD54(1-a4)/32 = p(2d)4[1-(d/2d)4]/32 = 1,472d4.
7.1. На первом участке угол закручивания в соответствии с законом Р.Гука равен:
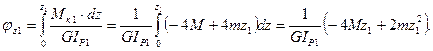
Угол закручивания изменяется по кривой второго порядка и на границах участка принимает значения
при z1= 0 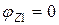 , при z1= 2l
, при z1= 2l 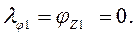
Определим выпуклость кривой 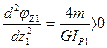 , следовательно кривая
, следовательно кривая 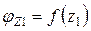 выпукла вниз.
выпукла вниз.
Условие экстремума кривой 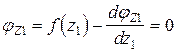 ,
,
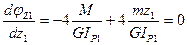 , следовательно функция
, следовательно функция 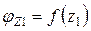 имеет экстремум при z1 = l.
имеет экстремум при z1 = l.
Вычислим угол закручивания
при z1 = l 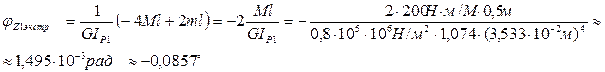
7.2 . На втором участке угол закручивания изменяется по кривой
второго порядка
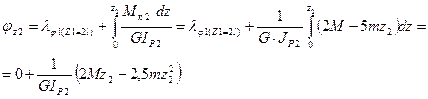
Угол закручивания на границах второго участка принимает значения
при z2=0 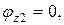 при z2=2l
при z2=2l 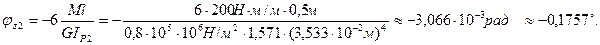
Определим выпуклость кривой 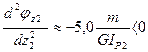 . Следовательно кривая
. Следовательно кривая 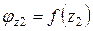 выпукла вверх.
выпукла вверх.
Условия экстремума кривой 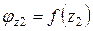
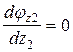
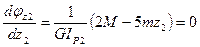 .
.
Следовательно функция 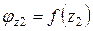 имеет экстремум при z2=0,4l. Вычислим угол закручивания при z2=0,4l
имеет экстремум при z2=0,4l. Вычислим угол закручивания при z2=0,4l
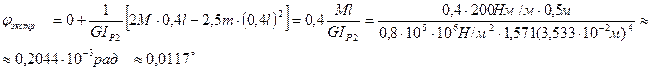
7.3. На третьем участке угол закручивания равен: 
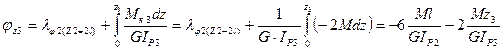
при z3=0 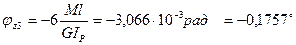 ,
,
при z3= l 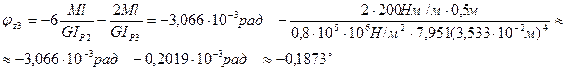
7.4. Угол закручивания на четвертом участке равен:
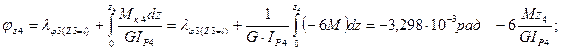
при z4=0 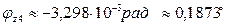 ,
,
при z4=l 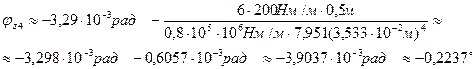
7.5. На пятом участке угол закручивания изменяется по кривой
второго порядка:
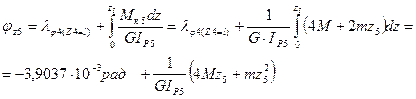
Угол закручивания на границах пятого участка принимает значения
при z5=0 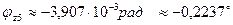 ;
;
при z5=2l 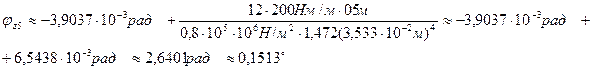
Определим выпуклость кривой 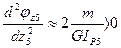 . Следовательно кривая
. Следовательно кривая 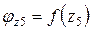 выпукла вниз. Условие экстремума кривой:
выпукла вниз. Условие экстремума кривой:
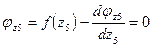 ,
, 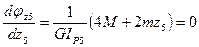 . Следовательно, функция
. Следовательно, функция 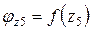 имеет экстремум за пределами (z5 = -2l) пятого участка. По результатам вычислений строится эпюра углов закручивания j по длине вала (рис. 1, г).
имеет экстремум за пределами (z5 = -2l) пятого участка. По результатам вычислений строится эпюра углов закручивания j по длине вала (рис. 1, г).
8. В классе ПЭВМ кафедры студент реализует машинный вариант выполнения РПР, сопоставляет результаты традиционного и машинного расчетов.
9. В соответствии с расчетными данными выполняется эскиз вала.
